Vergleich Solargewinne: Rechnung Meier - Messung Bossert - EnEV
1. Vorbemerkung
Es ist schon lange bekannt, daß mit dem Wissen der Bauphysik der Heizwärmebedarf aus Wetterverlauf, Daten der Gebäudehülle und Innenraumklima richtig berechnet werden kann. Es gibt aber eine Gruppe (Paul Bossert, Claus Meier und andere), die diese Kenntnisse bestreitet, durch die eigenen Behauptungen ersetzt wissen will und Messungen fordert, die dann angeblich die eigenen Behauptungen bestätigen und die "offizielle" Bauphysik widerlegen würde.
Nun sind diese Messungen [2] von einem Mitglied dieser Gruppe gemacht worden (Paul Bossert) und haben die richtige Bauphysik bestätigt, wie die durchgeführten Messungen zeigen und wie zu erwarten war.
Wer nur einen Überblick über diesen Sachverhalt haben wollte, hat das schon in der Kurzfassung gelesen. Je tiefer jemand einsteigen will, desto mehr sollte er hier lesen.
Der Rest dieser Abhandlung skizziert die Behauptungen Meiers, einige Fehler in seinen Abhandlungen und stellt den falschen die richtigen Betrachtungen gegenüber. Außerdem wird gezeigt, wie aus den Messungen relevante Kennwerte gewonnen werden und besteht aus:
2. Solargewinn nach Meier
2.1 Meiers eigenartige Mittelwertbildung
2.2 Beziehung zwischen Meiers Mittelwert und dem sinnvollen Mittelwert
2.3 Auswertung von Meiers keff mit den Daten der EMPA-Untersuchung
3. Bestimmung des Solargewinnfaktors nach der EnEV
4. Negative keff und Perpetuum Mobile bei Meierschen Solargewinnen
5. Auswertung der Bossert'schen Messung
6. Vergleich der Solargewinne nach Messung Bossert mit den Rechnungen Meier bzw. EnEV
In der Abhandlung sind folgende
Bilder:
Bild 1: Mittelwerte Meier und üblich
Bild 2: Wetterdaten
Bild 3: keff-Verlauf
und Tabellen:
Tabelle 1: Solargewinnfaktor nach Meier
Tabelle 2: Solargewinnfaktor nach der EnEV
Tabelle 3: Meßwerte Bossert (EMPA)
Tabelle 4: Daten der Wände
Tabelle 5: Streuung der Meßwerte
Tabelle 6: Wärmemengen einschließlich Streuung
Tabelle 7: Temperaturabweichungen, die die Streuungen erklären
Tabelle 8: Zusammenstellung der Wanddaten
Tabelle 9: Vergleich der Solargewinnfaktoren
2. Solargewinn nach Meier
Ausgangspunkt ist [1] Seite 6.5(60). Dort steht (hier blau gefärbt und ohne die Gleichungsnumerierung):
6.5.2.5 Solargewinnfaktor
Ein k-Wert-Bonus Δk in W/m2K als Differenz kann auch als Abminderungsfaktor für den k-Wert formuliert werden. Allgemein gilt dann die Formel 6.3.3 auf Seite 6.3(3):
(1)![]() keff= k × SW (W/m2K)
keff= k × SW (W/m2K)
keff = effektiver Wärmedurchgangskoeffizient (W/m2K)
k = Wärmedurchgangskoeffizient (W/m2K)
SW = Solargewinnfaktor der Wand
Auf Seite 6.5(61 und 62) steht dazu:
....damit wird dann der zusammengefaßte Ausdruck, die Formel 6.5.23, gefunden:
(2)![]() SW = 1-
SW = 1- 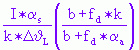
SW = Solargewinnfaktor der Wand (-)
k = Wärmedurchgangskoeffizient (W/m2K)
I = Strahlungsintensität der Sonne (W/m2)
αs = Strahlungsabsorptionsgrad (Absorptionszahl, Schluckwert) (-)
ΔθL = Temperaturdifferenz zwischen innen und außen (K)
fd = Faktor, der den mitwirkenden Speicherquerschnitt der Konstruktion sowie die entsprechende Wärmeflußzeit berücksichtigt
b = Wärmeeindringkoeffizient (Wh0,5/m2K)
αa = äußerer Wärmeübergangskoeffizient (W/m2K)
2.1 Meiers eigenartige Mittelwertbildung
Vor der weiteren Auswertung der Gleichungen (1) und (2) ist eine Vorbemerkung zu Meiers eigenartiger Mittelwertbildung zu machen.
Dazu folgendes Zitat aus [4] oder hier:
Welche absorbierten Solarstrahlungen sind in etwa anzusetzen?
In Anlehnung an die Wärmeschutzverordnung von 1995 [5] werden als Strahlungsangebot die dort angegebenen Werte übernommen. Für eine Gradtagzahl von 3500 Kd, einer durchschnittlichen Temperaturdifferenz von Δt = 15 K, einer Einstrahlungsperiode von zwölf Stunden und einem durchschnittlichen Strahlungsabsorptionsgrad von 0,6 ergeben sich absorbierte SoIarstrahlungswerte, die in der rechten Spalte der untenstehenden Tabelle 2 zusammengestellt sind.
Die in der vierten Spalte aufgeführten StrahIungswerte sind in Bild 4 markiert und werden in Tabelle 3 berücksichtigt, in der effektive k-Werte für den Neu- und Altbau aufgelistet sind: Monolithische Wände erreichen dabei k-Werte, die durch den Solarbonus auch hier sogar gegen Null gehen können.
Tabelle 2: Das Strahlungsangebot unterschiedlicher Himmelsrichtungen
| WSchVO 95 | für 12 Stunden | as = 0,6 | |
| Südorientierung | 400 kWh/mēa | 143 W/mē | 85 W/mē |
| Ost- und Westorientierung | 275 kWh/mēa | 98 W/mē | 59 W/mē |
| Nordorientierung | 160 kWh/mēa | 57 W/mē | 34 W/mē |
Rechnen wir mal nach: 3500 Kd mit durchschnittlich Δt = 15 K ergibt d = 233 1/3 Tage (= 3500 Kd/15 K) - ein vernünftiger Wert für die Heizperiode von reichlich 7 Monaten. Da ein Tag 24 Stunden hat, dauert die Heizperiode 5600 h (= 233 1/3 Tage x 24 Stunden). Die 5600 h beziehen sich auf die Heizperiode bzw. die Heizperiode im Jahr - 5600 h/HP = 5600 h/a. Nun rechnen wir z.B. bei der Südorientierung weiter: 400 kWh/(mēa) durch 5600 h/a = 0,07143 kW/mē oder 71,4 W/mē. Holla - da stimmt doch was nicht?! In Meiers Tabelle steht doch der doppelte Wert: 143 W/mē (= 2 x 71,4 W/mē). Der Widerspruch klärt sich auf, wenn wir den Tabellenkopf betrachten: für Meier hat der Tag nur 12 Stunden - und schon ist der Widerspruch "erklärt". Zur Verdeutlichung das nachfolgende Bild:
Bild 1: Mittelwerte Meier und üblich
Durch diese ungewöhnliche Mittelwertbildung ist Meiers I gleich dem Doppeltem des Mittelwertes Id, wie die meisten Menschen einen Mittelwert bilden würden:
Anmerkung: In [6] Seite 108f schreibt Meier in Kapitel:
6.2.5 Fehlerhafte Forschungsmethodik
Die Ignoranz instationärer Verhältnisse führt bei der Beschreibung von Transmissionswärmeverlusten bedauerlicherweise auch zu einer falsch verwendeten Forschungsmethodik.
Bei der Bewertung von speicherfähigen Massivwänden (Schwerbauweise) und von Dämmstoffkonstruktionen (Leichtbauweise) wird von offizieller Bauphysikseite die Meinung vertreten, beide würden energetisch etwa gleichrangig einzustufen sein. Dies stimmt jedoch nur, wenn für die Energiebilanzierung die Systemgrenze des Gebäudes auf der Innenseite der Außenhülle zu liegen kommt (die Tapetengrenze). Nur so kann die eingespeicherte Solarenergie einer massiven Wand ausgegrenzt und dann (fälschlicherweise) angenommen werden, die Transmissionswärmeverluste fänden durch einen, auch gemessenen, k-Wert (U-Wert) hinreichend Berücksichtigung. Eine solche Systemabgrenzung entspricht jedoch nicht der Realität. Die Systemgrenze gehört nach außen, denn ein Gebäude steht draußen im Freien und genießt auch die energetischen Segnungen der Sonne, die dann natürlich auch mit in die Überlegungen einbezogen werden müssen - wo doch die Nutzung von Solarenergie so groß im Gespräch ist!
Und deshalb wird nun ständig evaluiert. Eine Evaluierung" ist jedoch überhaupt kein strenger wissenschaftlicher Beweis, sondern heißt nur Abschätzung, Taxierung; man schwebt also im Vermutungsbereich. Zur Evaluierung" des k-Wertes (U-Wertes) wird stets auf die gemessene Wärmestromdichte an der Innenoberfläche der Außenwand hingewiesen, die ja nun exakt" den verlorengegangenen Wärmestrom angeben würde. Im Bild 6.5 wäre dies der Punkt (2). Es wird jedoch dabei vergessen, daß ein in die Wand hineingehender Wärmestrom nicht automatisch auf der anderen Seite wieder hinausgeht. Diese Annahme stimmt nur für den Beharrungszustand, also bei konstanter Wärmestromdichte im gesamten Bauteil und geradliniger Temperaturverteilung in einer Bauteilschicht. Aber dies ist illusionär. Hier muß auf Bild 6.4 hingewiesen werden, das die Temperaturgradienten im instationären Temperaturzustand verdeutlicht.
Die Messung des inneren Wärmestromes beschreibt somit nicht die wirklichen Wärmestromverhältnisse in der gesamten Außenwand. Sie ist jedoch bei /Hauser 81/, /Kupke 87/, /Möhl 84/ und auch in /IBP 96a/ zur Grundlage der Forschungsarbeit gemacht worden. Immer wurden hier die inneren Wärmestromdichten gemessen und dann extrapoliert". Es ist verständlich, daß bei derartigen methodischen Fehlern nichts Vernünftiges herauskommen kann (9).
Ein solches Vorgehen bedeutet Mißbrauch der Wissenschaft und im Endeffekt sogar Betrug am Kunden und sollte Anlaß sein, Forschungsarbeiten zu mißtrauen und genauer unter die Lupe zu nehmen.
Betrug liegt hier nicht vor. Was aber ganz bestimmt vorliegt, ist Unwissenheit. Jedoch nicht seitens der Wissenschaft, sondern seitens Meier. Meiers Ausführungen erinnern mich an die Frage von den zwei gleichgroßen Flaschen: in einer ist Rotwein, in der anderen Wasser. Jetzt wird ein Löffel Wein aus der Weinflasche in die Wasserflasche geschüttet und dann ein Löffel des Wein-Wasser-Gemisches zurück in die Weinflasche. Frage: ist mehr Wasser im Wein oder mehr Wein im Wasser? Die Beantwortung erscheint erscheint sehr kompliziert, wenn man sich der vorgegebenen Denkweisen bedient - ist aber sehr einfach, wenn man nur das Ergebnis betrachtet: natürlich ist in beiden gleichviel - denn in beiden Flaschen ist das gleiche Volumen wie vor dem Mischen - also muß die ausgetauschte Menge gleich sein.
Und hier stellen wir uns zwei Systemgrenzen vor: eine in der genannten Tapetenebene und eine an der Außenwand (oder auch an beliebiger Stelle in der Außenwand). Die Wärmeströme in der inneren und äußeren Ebene sind natürlich fast nie gleich, weil zwischen beiden Ebenen der speichernde Teil Wand liegt. Aber wenn man ganz lange Zeiten betrachtet (z.B. eine ganze Heizperiode), so müssen die Energien, die durch beide Ebenen geflossen sind, fast gleich sein. Denn zumindest Meier akzeptiert den Energieerhaltungssatz - und die Änderung der gespeicherte Energiemenge in der Wand ist sehr gering, da die Temperaturverteilung in der Wand zu Beginn und Ende der Heizperiode fast gleich ist.
Und noch ein Vergleich: Für die Energie soll stellvertretend Wasser betrachtet werden. Das Wasser soll in einem Gefäß sein (entspricht der Energie in der Wand), das unten ein Loch hat (entspricht Innenwandoberfläche), wo das Wasser (entspricht Energie) relativ gleichmäßig ausfließt. Von oben wird Wasser eingegossen(entspricht z.B. Solarenergie) und auch wieder entnommen (entspricht z.B. nächtliche Abstrahlung). Ganz gleich wieviel Wasser oben eingegossen und entnommen wird - ganz gleich wie die Wasserstandshöhe bzw. Wassermenge in dem Gefäß ist - die Summe von eingegossenen und entfernten Wasser ist fast gleich dem unten ausgelaufenen Wasser. Und wenn die Wasserstandshöhe zu Anfang und Ende gleich ist, sind die Mengen nicht nur fast gleich, sondern genau gleich. Damit ist es unerheblich, an welcher Stelle die Systemgrenze betrachtet wird.
2.2 Beziehung zwischen Meiers Mittelwert und dem sinnvollen Mittelwert
Damit können wir uns wieder den Mittelwerten zu wenden. Da die Mittelwerte nur über lange Zeiten stimmen, ist die Meiersche Mittelwertbildung als nicht gerade hilfreich zu betrachten, die gewöhnliche Mittelwertbildung ist viel zweckmäßiger. Zwischen dem Meierschen Mittelwert (der nicht konstant ist, sondern in der Hälfte der Zeit 0 ist) und einem sinnvollen Mittelwert besteht also folgende Beziehung:
(3)![]() I = 2 * Id
I = 2 * Id
2.3 Auswertung von Meiers keff mit den Daten der EMPA-Untersuchung
Um weitere Erkenntnisse zu gewinnen, wird die Formel des zweiten Zitats (2) in die Formel des ersten Zitats (1) eingesetzt:
(4)![]() keff = k × SW = k -
keff = k × SW = k - 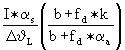
![]() (W/m2K)
(W/m2K)
Durch Multiplikation mit der Temperaturdifferenz ΔθL erhält man die Wärmestromdichte q. Anschließend wird auch (3) berücksichtigt:
(5)![]() q = keff ×ΔθL = k ×ΔθL − I
q = keff ×ΔθL = k ×ΔθL − I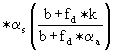 =
=
![]()
![]() = k ×ΔθL − I × ηMeier-U = k ×ΔθL − 2 * Id × ηMeier-U = k ×ΔθL − Id × ηMeier
= k ×ΔθL − I × ηMeier-U = k ×ΔθL − 2 * Id × ηMeier-U = k ×ΔθL − Id × ηMeier ![]() (W/m2)
(W/m2)
Gleichung (5) wird hier kontrolliert. Außerdem sind in (5) sind folgende Faktoren eingeführt:
(6)![]() ηMeier-U =
ηMeier-U = 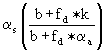
![]() ηMeier = 2 * ηMeier-U
ηMeier = 2 * ηMeier-U![]() ηMeier =
ηMeier = 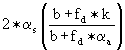
![]() (-)
(-)
η ist der Anteil von der einfallenden Strahlung, der heizswärmestrommindernd wirkt. Hier sind alle mir bekannten Meierschen Tabellen aufgeführt - einschließlich der richtigen Werte und Kennzeichnung der Werte, wo Meier negative Werte in seinen Tabellen stören. Dort er kurzerhand diese negativen keff-Werte zu Null gesetzt - aber das nicht extra erwähnt - sicher um den "unmündigen Leser" nicht zu verwirren..
Beispiel:
Meier definiert folgende Werte fd = 7,63 h0,5 (Seite 6.5(24)) und αa = 17,5 W/mē K (Seite 6.5(72)) Die anderen Werte sind aus [2], eine Untersuchung, die vor allen Dingen auf Veranlassung und Mitarbeit von Paul Bossert (einem Mitkämpfer Meiers) geschehen ist.
In der Untersuchung sind 2 Wände (massiv -WDVS) verglichen worden:
Bezüglich b ist nur der bestimmende Unterschied Mauerwerk und Dämmung genannt:
Tabelle 1: Solargewinnfaktor nach Meier
| Wert | massive Wand | WDVS |
| λ | 0,195 W/(m K) | 0,040 W/(m K) |
| ρ | 1100 kg/mģ | 16 kg/mģ |
| c | 0,26Wh/(kg K) | 0,39Wh/(kg K) |
| k | 0,38 W/(mēK) | 0,39 W/(mēK) |
| αs | 0,711 | 0,711 |
| αa | 17,5 W/(mēK) | 17,5 W/(mēK) |
| fd | 7,63 h0,5 | 7,63 h0,5 |
| b | 7,47 Wh0,5/(mē K) | 0,50 Wh0,5/(mē K) |
| fd*k | 2,90 Wh0,5/(mē K) | 2,98 Wh0,5/(mē K) |
| fd*αa | 133,53 Wh0,5/(mē K) | 133,53 Wh0,5/(mē K) |
| ηMeier | 10,46% | 3,68% |
3. Bestimmung des Solargewinnfaktors nach der EnEV
Interessant ist der Wert von ηEnEV nach der EnEV, also Formel DIN V 4108-6, Formel (60):
(7)![]() Qs, op = U Aj Re (α Isj − Ff hr ΔΘer) t
Qs, op = U Aj Re (α Isj − Ff hr ΔΘer) t
Nach Division durch Aj und t folgt bei Vernachlässigung der nächtlichen Abstrahlung (d.h. z.B. mit Ff = 0), wird:
(8)![]() ηEnEV = U Re αs
ηEnEV = U Re αs
mit Re = 0,04 mē K/W (Standardwert) bzw. αa (Wert Meier) wird:
Tabelle 2: Solargewinnfaktor nach der EnEV
| Wert | massive Wand | WDVS |
| U | 0,38 W/(mēK) | 0,39 W/(mēK) |
| αs | 0,711 | 0,711 |
| Re | 0,04 mēK/W | 0,04 mēK/W |
| αa = 1/Re | 25,0 W/(mēK) | 25,0 W/(mēK) |
| ηEnEV | 1,08% | 1,11% |
| αa | 17,5 W/(mēK) | 17,5 W/(mēK) |
| Re = 1/αa | 0,06 mēK/W | 0,06 mēK/W |
| ηEnEV | 1,54% | 1,58% |
4. Negative keff und Perpetuum Mobile bei Meierschen Solargewinnen
Aus den vorstehenden Rechnungen ergeben sich interessante Sachverhalte:
5. Auswertung der Bossert'schen Messung
Vor dem Vergleich der verschiedenen Solargewinnne sind die gemessenen Werte des Meierfreundes Bossert auszuwerten, damit nur Vergleichbares verglichen wird.
Auf Seite 17 von [2] stehen die Tabelle 10 bis 12 mit den mittleren Meßwerten und den mittleren Meßdaten. Da Monatswerte angegeben sind, ist die Zeit gegenüber der Einschwingzeit der Wände genügend groß. Die Einschwingzeiten der Wände betragen etwa 5 Tage (Massivwand) bzw. 3 Tage (WDVS-Wand) ([2], Seite 10, Bild 8).
Diese Auswertung wird in Form von Tabellen dargestellt. Im Kopf der nachfolgenden Tabelle sind die Meßwerte aus [2] Tabelle 10 bis 12. Die Perioden sind die aufeinanderfolgenden Meßmonate. Die weiteren Spalten sind:
ΘaMonatsmittelwert der Außentemperatur
Isüd Monatsmittelwert der Solarstrahlung
ΘM Monatsmittelwert der Temperatur in der Meßzelle mit Massivwand
qM Monatsmittelwert des Wärmestrom in der Innenseite der Massivwand
ΘWDVS Monatsmittelwert der Temperatur in der Meßzelle mit WDVS-Wand
qWDVS Monatsmittelwert des Wärmestrom in der Innenseite der WDVS-Wand
Tabelle 3: Meßwerte Bossert (EMPA) [2, Tabellen 10 bis 12 (Seite 17)]
| massive Wand | WDVS | |||||
| Periode | Θa | Isüd | ΘM | qM | ΘWDVS | qWDVS |
| Nov 91 | 2,1°C | 15,2 W/mē | 21,86°C | 6,945 W/mē | 22,38°C | 7,540 W/mē |
| Dez 91 | 0,1°C | 34,3 W/mē | 21,73°C | 7,971 W/mē | 22,32°C | 8,460 W/mē |
| Jan 92 | -0,7°C | 60,7 W/mē | 21,70°C | 7,514 W/mē | 22,30°C | 8,021 W/mē |
| Feb 92 | 1,6°C | 89,6 W/mē | 21,79°C | 6,283 W/mē | 22,39°C | 6,789 W/mē |
| Mrz 92 | 6,3°C | 86,9 W/mē | 22,02°C | 4,587 W/mē | 22,59°C | 5,215 W/mē |
| Apr 92 | 9,2°C | 102,0 W/mē | 22,15°C | 3,362 W/mē | 22,73°C | 3,958 W/mē |
Gleichung (5) kann auch folgendermaßen geschrieben werden:
(9)![]() q = U × (Θa − Θi) − I × η
q = U × (Θa − Θi) − I × η
In (9) sind U und η zunächst unbekannt, während die restlichen Größen die bekannten Meßwerte sind. Da nur 2 Größen unbekannt sind, aber 6 Gleichungen dafür vorliegen, ist das Gleichungssystem überbestimmt, d.h. nicht alle Gleichungen können erfüllt werden - es bleiben Restabweichungen. Die Lösung wird so gesucht, daß die Restabweichungen minimal werden. Das Rechenverfahren ist in [3] beschrieben. Aber auch ohne Kenntnis des Rechenverfahrens kann man mit den ermittelten Werten für U und η arbeiten, die in der nächsten Tabelle angegeben sind.
| massive Wand | WDVS | |
| U | 0,377 W/(mēK) | 0,389 W/(mēK) |
| η | 1,48% | 1,33% |
| c' | 143 Wh/(mēK) | 62 Wh/(mēK) |
Die Werte von U sind unproblematisch - die Meßwerte stimmen mit den berechneten [2], Seite 5, Tabelle 1) und den stationär ermittelten ([2], Seite 11, Tabelle 6) Werten überein.
In Tabelle 4 sind auch mit c' die Wärmekapazitäten der Wände angegeben. Diese Werte sind mit den Werten der Tabelle 1, Seite 5 von [2] berechnet. Die Abweichungen zwischen Rechenwerten nach (9) und den Meßwerten sind anschließend aufgeführt (absolut und relativ).
Tabelle 5: Streuung der Meßwerte
| Periode | ΘM | qM | ΘWDVS | qWDVS |
Abweichung der Anpassung |
Abweichung relativ |
Abweichung der Anpassung |
Abweichung relativ |
|
| Nov 91 | -0,278 W/mē | -4,01% | -0,139 W/mē | -1,84% |
| Dez 91 | 0,326 W/mē | 4,09% | 0,280 W/mē | 3,31% |
| Jan 92 | -0,030 W/mē | -0,40% | -0,112 W/mē | -1,40% |
| Feb 92 | 0,000 W/mē | 0,01% | -0,102 W/mē | -1,51% |
| Mrz 92 | -0,051 W/mē | -1,10% | 0,036 W/mē | 0,70% |
| Apr 92 | -0,008 W/mē | -0,23% | 0,052 W/mē | 1,31% |
Da der mittlere Wärmestrom bekannt ist, kann mit der Monatsdauer die Wärmemenge bestimmt werden. Mit den bereits bestimmten Abweichungen, kann die Unsicherheit der Wärmemenge bestimmt werden.
Tabelle 6: Wärmemengen einschließlich Streuung
| massive Wand | WDVS | |||
|
Wärmedurchgang |
Abweichung absolut |
Wärmedurchgang |
Abweichung absolut |
| Nov 91 | 5,00 kWh/mē | -200,3 Wh/(mēK) | 5,43 kWh/mē | -100,1 Wh/(mēK) |
| Dez 91 | 5,93 kWh/mē | 242,6 Wh/(mēK) | 6,29 kWh/mē | 208,5 Wh/(mēK) |
| Jan 92 | 5,59 kWh/mē | -22,3 Wh/(mēK) | 5,97 kWh/mē | -83,4 Wh/(mēK) |
| Feb 92 | 4,37 kWh/mē | 0,3 Wh/(mēK) | 4,73 kWh/mē | -71,2 Wh/(mēK) |
| Mrz 92 | 3,30 kWh/mē | -36,4 Wh/(mēK) | 3,88 kWh/mē | 27,1 Wh/(mēK) |
| Apr 92 | 2,42 kWh/mē | -5,5 Wh/(mēK) | 2,85 kWh/mē | 37,5 Wh/(mēK) |
Daraus werden als Letztes mit den Wärmekapazitäten die Unsicherheiten der Temperaturverteilung zu Beginn und Ende jeder Periode in der Dicke der Wand bestimmt. Die Unsicherheit der Temperaturverteilung liegt deutlich unter 2 K (bis auf Dez. 91 beim WDVS) - und damit in einem plausiblen Bereich, d.h. die Abweichungen des Wärmestrom von Gleichung (8) ließen sich allein durch die Änderung der gespeicherten Wärmemenge erklären, obwohl es noch weitere Unsicherheiten gibt, die alle in [2] aufgeführt sind.
Tabelle 7: Temperaturabweichungen, die die Streuungen erklären
| Temperaturabweichung | ||
| massiv | WDVS | |
| Nov 91 | -1,4 K | -1,6 K |
| Dez 91 | 1,7 K | 3,4 K |
| Jan 92 | -0,2 K | -1,3 K |
| Feb 92 | 0,0 K | -1,1 K |
| Mrz 92 | -0,3 K | 0,4 K |
| Apr 92 | 0,0 K | 0,6 K |
Eine Übereinstimmung zu den Meßwerten kann auch durch passende Wahl eines Rea hergestellt werden. Das ist zulässig, da Re z.B. auch vom Wind abhängt. (in [2] S.30 erwähnt: "Die verwendeten Modelle zum konvektiven Wärmeübergang an Aussenwänden sind zu verbessern.").
Tabelle 8: Zusammenstellung der Wanddaten
| Wert | massive Wand | WDVS |
| U | 0,38 W/(mēK) | 0,39 W/(mēK) |
| αs | 0,711 | 0,711 |
|
Meßwert |
1,48% | 1,33% |
| Rea | 0,055 mēK/W | 0,048 mēK/W |
| 1/Rea (αa) | 18,2 W/(mēK) | 20,8 W/(mēK) |
Zum Vergleich: Die EnEV verwendet den Wert Rea = 0,04 mēK/W (25 W/(mēK)), Meier verwendet den Wert Rea = 0,057 mēK/W (17,5 W/(mē K)). Die Meßwerte bei der Bossert'schen Messung liegen zwischen den beiden Werten. Die Abweichungen sind auch verständlich, denn Rea hängt von der Art der Oberfläche und den Windverhältnissen ab. Deswegen ist kein Wert falsch, sondern in jedem konkreten Fall richtig, bzw. als sinnvolle Annahme richtig.
Anmerkung: Wo Meier keine Fehler macht, konstruiere ich auch keine Fehler. Meine Veröffentlichungen bezüglich Meier beziehen nur auf dessen Fehler. mit denen er Laien (und leider manchmal auch Fachleute) verunsichert.
6. Vergleich der Solargewinne nach Messung Bossert mit den Rechnungen Meier bzw. EnEV
Nachfolgend sind die verschiedenen η aufgeführt:
Tabelle 9: Vergleich der Solargewinnfaktoren
| Quelle | massive Wand | WDVS |
| Messung | 1,48% | 1,33% |
| Rechnung Meier | 10,46% | 3,68% |
| EnEV (Standard) | 1,08% | 1,11% |
| EnEV (αa = 0,06) | 1,54% | 1,58% |
Wie zu sehen ist, sind die Rechenwerte Meier selbst bei Berücksichtigung von Toleranzen viel zu hoch, während die EnEV-Werte mit den Meßwerten verträglich sind.
Aber etwas anderes ist ganz wesentlich: Die Voraussagen aus der exakten Theorie sagen (die auch der EnEV zu Grunde liegen), daß bei genügend langer Zeit der Solargewinn unabhängig von der Speichermasse wird. Ganz gleich, wie der Wert von Re ist - er ist bei den beiden untersuchten Wänden gleich. Und die Messung zeigt, daß das auch in der Praxis der Fall ist - entgegen der Theorie von Meier.
Auch der übliche Ausrede von Meier, daß die Meßwerte von der Dämmindustrie manipuliert wurden, klappt hier nicht, da ja Bossert an den Messungen beteiligt war.
Noch eine Anmerkung: Wie sinnlos Effektivwerte sind, zeigen die nachfolgenden Diagramme. Das gilt nicht nur für den Meierschen Unsinn, sondern auch analog für die effektiven Werte. die z.B. in der EnEV bei Fenstern benutzt werden - und wo das teilweise auch in die Daten eingerechnet wird. Es kommen für den Gesamtverbrauch zwar gleiche Werte heraus, da mit standartisiertem Wetter gerechnet wird, aber die Ergebnisse sind nur schwer auf ein reales Wetter anzupassen.
Für die Berechnung von keff werden die Werte U = 0,38 W/(m2 K), η = 1,4 % und eine Innentemperatur von θ = 22°C benutzt, die etwa den Werten der benutzten Wände entsprechen.. Als Wetterdaten werden für die Monate November bis April die Wetterdaten des Untersuchungsberichts benutzt:
Bild 2: Wetterdaten
Aus diesen Wetterdaten folgen die nachfolgenden keff-Verläufe − gemessen von Bossert (EMPA) und berechnet mit richtigen und falschen Rechenvorschriften:
Bild 3: keff-Verlauf
Daß die Meßergebnisse die Meierschen Behauptungen vollkommen widerlegen, ist aus den obigen Kurven zu sehen - bei dem gewählten keff-Bereich liegen die unsinnigen keff-Werte teilweise außerhalb des dargestellten Bereichs. Beachtlich: die Unterschiede zwischen Rechenwerten nach der EnEV und den Meßergebnissen sind innerhalb der Toleranzen der Messung.
Literatur:
[1] Meier, C.: Wärmeschutzplanung für Architekten und Ingenieure. 4. Lieferung März 1997. Rudolf-Müller-Verlag Köln
[2] Viele, u.a. Bosser, P: Energiebilanz von Außenwänden unter realen Randbedingungen. Untersuchungsbericht EMPA Nr. 136788. Dez. 1994
[3] Schwarz, H. R.; Rutishauser, H.; Stiefel, E.: Numerik symmetrischer Matrizen BSB B.G. Teubner Verlagsgesellschaft, Stuttgart 1968
[4] Meier, C.: Gut gespeichert ist auch gut gedämmt. db deutsche Bauzeitung 133 (1999) Nr. 5, S. 138 - 146
[5] Entwurf der ŧVerordnung über einen energiesparenden Wärmeschutz und eine energiesparende Anlagentechnik bei GebäudenŦ (EnergiesparV), Dez. 97
[6] Meier, C.: Richtig bauen. - Bauphysik im Widerstreit - Probleme und Lösungen. expert verlag GmbH, Renningen, 2001, ca. 250 S., 72 Abb., 16 Tab.
letzte Änderung: 09.04.2004