Zusatzinformationen zu k_eff

1. Zu Mittelwerten

Es gibt verschiedene Arten von Mittelwerten. Am Beispiel einer Autofahrt soll das gezeigt werden.

Die Strecke soll 200 km lang sein, der Fahrer fährt 100 km mit 25 km/h und 100 km/h. Wie groß ist die Durchschnittszeit einer Teilstrecke und wie groß ist die Durchschnittsgeschwindigkeit.

Fahrzeit der ersten Teilstrecke 4h (= 100 km/25 km/h), Fahrzeit der zweiten Teilstrecke 1h (= 100 km/100 km/h). Die Gesamtfahrzeit ist also 5 Stunden - oder für jede Teilstrecke 2,5 h:

Diese Art der Mittelwertbildung nennt sich arithmetisches Mittel.

Die Durchschnittsgeschwindigkeit oder der Mittelwert wäre so nicht zu berechnen:

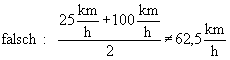
Denn für die 200 km wurden 5 Stunden gebraucht und 5 Stunden für 200 km bedeuten eine Durchschnittgeschwindigkeit von 40 km/h (= 200 km/5 h). Wie ist also hier die Durchschnittsgeschwindigkeit zu berechnen?

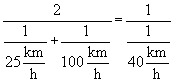
Diese Art der Mittelwertbildung nennt sich harmonisches Mittel.

Daneben sind noch der geometrische Mittelwert und weitere Mittelwerte bekannt und haben jeweils ihre speziellen Anwendungszwecke. Allerdings ist der Meiersche Mittelwert doch sehr ungewöhnlich.

2. Kontrolle

Aus

folgt durch Integration über die Zeit:

Die letzte Gleichungsumformung ist zulässig, weil U und η zeitunabhängig sind.

Wenn Δθ und I_d zeitunabhängig ist (und eine Heizperiode betrachtet wird mit der Zeitdauer t_HP), können die Integrale als Produkte geschrieben werden.

Wenn auch Δθ und I_d konstant sind, können die Integrale wieder in Produkte umgewandelt werden. Damit wird:

Wie diese Kontrolle aussehen soll bei dem Meierschen k_eff ist mir nicht klar, denn dann müßte nachts ein anderes k_eff als am Tage gelten. Ich glaube kaum, daß Meier das erklären kann. Mit Δθ = 15 K, I_d = 71,4 W/m² und t_HP = 5600 h = 233 1/3 d (Tage) ergibt sich:

also genau die Werte von denen Meier ausgegangen ist.

3. k_eff-Hyperbel

Aus der für beliebige Werte von U, η, Δθ und I_d gültigen Gleichung, die auch für beliebige Werte ein sinnvolles Ergebnis ergibt

wird bei Division durch Δθ ein k_eff, daß man nicht für beliebige Werte von Δθ und I_d als sinnvoll bezeichnen kann:

Der zweite Term ist eine Hyperbelfunktion. Eine Hyperbelfunktion hat eine Unstetigkeitsstelle (hier bei Δθ = 0). Bei kleineren Werten von Δθ kann k_eff negativ werden - und dieser Teil ist sowohl mathematisch richtig als auch physikalisch sinnvoll. Dieser Fall liegt z.B. oft bei Fenstern vor: Es muß zwar noch geheizt werden (d.h. die Außentemperatur ist niedriger als die Innentemperatur), aber durch die Fenster kommt durch die Sonnenwärme mehr Energie herein als durch Transmission verloren geht. Bei Wänden dürfte dieser Fall kaum eintreten - wenn k_eff negativ werden könnte, braucht nicht mehr geheizt zu werden.

Aber trotzdem mal die Funktion von k_eff mit den Wetterdaten der EMPA-Untersuchung bis April, Mai bis Juli mit sinnvollen Phantasiedaten:

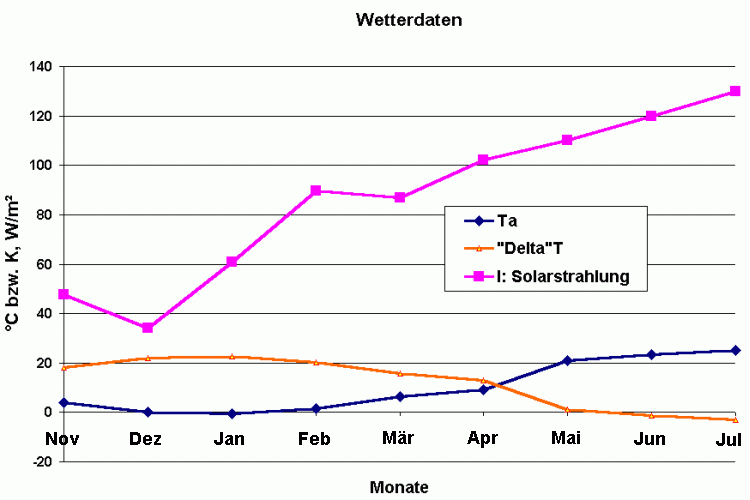
Mit diesen Wetterdaten ergibt sich:

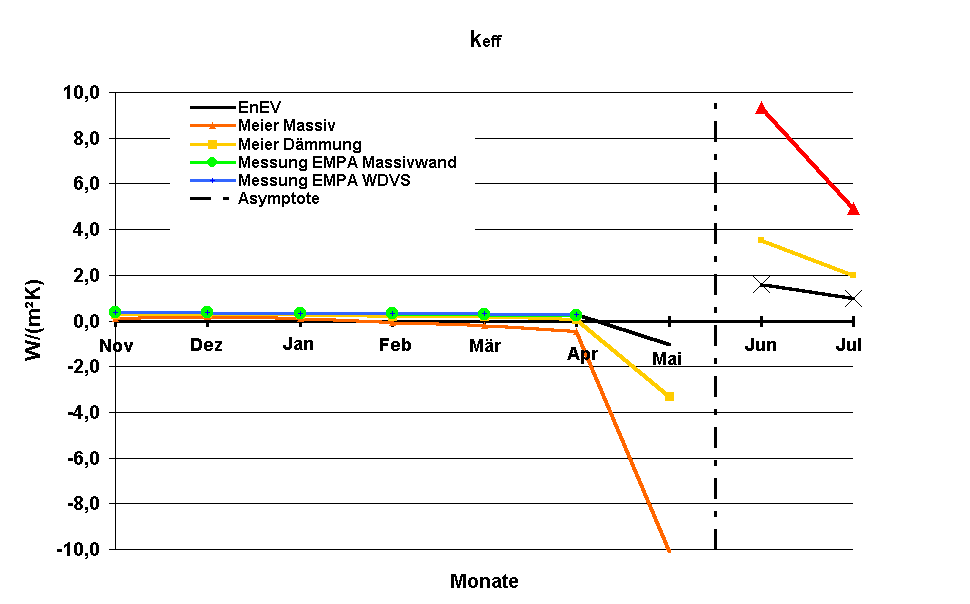
Für negative Werte von Δθ wird k_eff wieder positiv - daß ist mathematisch zwar richtig, aber heiztechnisch sinnlos.

letzte Änderung: 25.04.2004

Impressum, Disclaimer