- Vorbemerkungen
- Übertragung von Definitionen auf andere Zwecke
- Aufstellung der Wärmeleitungsgleichung
- Die Wärmeleitungsgleichung in Vektorschreibweise
- Vereinfachungen
- Anfangs- und Randbedingungen
- Lösungsansatz
- Beispiellösung
- Auswertung der Existenz einer Lösung
- Die Wärmespeicherung der Wand und die Konsequenzen
- Die Zeitabhängigkeit der gespeicherten Wärme
- Betrachtung über einen Zeitabschnitt
- Heizenergiebedarf mit dem Mittelwertsatz der Integralrechnung
- Stationäre Betrachtungen
- U-Wert-Bestimmung
- Speicherkonstante bestimmen
- Periodische Betrachtungen
- Transmissionsmehrbedarf bei speicherarmen Wänden
- Ergänzungen
- Literatur
Über die Anwendbarkeit des U-Wertes (früher k-Wert) bestehen große Unklarheiten. Zitat aus der DIN [9, Abschnitt 4.2]: "Die Wärmespeicherfähigkeit der Bauteile geht bei strenger stationärer Betrachtung ...". Damit dürfte die Norm eigentlich nie angewandt werden, denn das Außenklima ist von Stationaritet weit entfernt. Das wird vereinzelt zum Anlaß genommen, die Anwendbarkeit vehement zu bekämpfen. Da sich der Heizenergieverbrauch bei modernen Bauweisen als kleine Differenz großer Zahlen ergibt, kann sich leicht eine große Abweichung zwischen Rechnung und tatsächlichen Verbrauch ergeben. Deshalb müssen die einzelnen Terme genau betrachtet werden. In diesem Artikel wird die Anwendbarkeit des U-Wertes bei instationärer Behandlung untersucht.
Selten wird die Linearität der Wärmevorgänge in Zweifel gezogen. Wie im weiteren gezeigt (z.B. Ende Abschnitt 4.2 oder Abschnitt 7) und auch in [18] und [19] ergänzt wird, ist es im Rahmen der Linearität für den Heizenergieverbrauch unwesentlich, ob die Wände Speicherwirkung haben oder nicht. Nur die Wärmestromschwankung auf der Innenseite der Wand ist bei geringer Speicherfähigkeit größer. Wesentlich für den Verbrauch ist der U-Wert. Wird die lineare Voraussetzng verlassen, sieht es anders aus. In der Übergangszeit tritt zeitweise ein Wärmeüberschuß auf. Wird der überschüssige Wärmeeintrag weggelüftet, so wird der Heizenergiebedarf größer, weil die weggelüftete Wärmeenergie ersetzt werden muß.
Eine weitere Quelle von Nichtlinearität ist die Zeit- und Temperaturabhängigkeit von Wärmeleitung und Speicherkapazität der Wandmaterialien. Die Zeitabhängigkeit der Materialien entsteht z.B. durch Veränderung des Feuchtegehalts. Ein weiterer Unsicherheitsfaktor ist das Nutzerverhalten. Z.B. können die eingestellten Temperaturen beim durchschnittlichen Nutzer durch den Wandaufbau beeinflußt werden. Ursachen könnten z.B. die trotz Heizleistungsregulierung (infolge des Wärmeübergangs an der inneren Wand auftretenden) größeren Wandtemperaturschwankungen sein.
Diese nichtlinearen Effekte sind wenig untersucht und auch nicht Gegenstand der vorliegenden Abhandlung. Zunächst wird erst einmal gezeigt, das eine in einem bestimmten Zusammenhang definierte Größe (hier z.B. der U-Wert bei stationären Bedingungen) auch in einem anderen Zusammenhang bedeutungsvoll sein kann (z.B. Bedeutung des U-Wert bei instationären Bedingungen).
Zunächst wird im Abschnitt 1 an einem Beispiel gezeigt, daß eine in einem bestimmten Zusammenhang definierte Größe (Flächenbegriff am Rechteck) auch in einem veränderten Zusammenhang bedeutungsvoll sein kann (Fläche bei unregelmäßiger Umrandung). Die Vorgehensweise im Beispiel der Fläche wird dann auf die Vorgehensweise für die Übertragung der Bedeutung des stationär definierten U-Wertes auf instationäre Bedingungen benutzt. Siehe Abschnitt 4.2 Gleichung (56) bzw. auf anderem Wege Abschnitt 5 Gleichung (71).
Diese Erweiterung der Bedeutung des U-Wertes ist das Hauptziel der Arbeit.
Zur Definition des U-Wertes gehören die Wärmeübergangswiderstände a i und a a für die Innen- und Außenseite der Wand. Der Wert der Wand selbst hat meistens den Formelbuchstaben R. Da die Wärmeübergangswiderstände praktisch speicherlos und transparent sind, vereinfacht deren Vernachlässigung die Ableitungen, ohne sie zu verfälschen. Deshalb wird der R-Wert der Einfachheit halber in dieser Arbeit mit U bezeichnet.
Eine Fläche ist als Produkt von Breite und Länge definiert und das betrifft nur das Rechteck. Da Breite und Länge jeweils in m gemessen werden, ist die Maßeinheit der Fläche m2. Auch der Kreis hat eine Fläche, aber die vorstehende Definition ist so nicht anwendbar. Indem man in den Kreis viele kleine Rechtecke einzeichnet und deren Flächen addiert, erhält man die Kreisfläche nur näherungsweise, da mit Rechtecken nicht die ganze Fläche bedeckt werden kann. Indem man die Restflächen mit immer kleineren Rechtecken ausfüllt, kommt man der gesamten Kreisfläche immer näher. Auf diese Art kann man die Definition der Rechteckfläche auf beliebig geformte Flächen übertragen.
Per Definition (oder komplizierter Rechnung, wenn man den Kreisumfang mit dem Radius definiert U = 2p r) hat der Kreis eine Fläche von A = p r2. Die Bestimmung der so definierten Zahl p ist ein kompliziertes Unterfangen. Auf geometrischen Wege stand dabei z.B. die Aufgabe, den Kreis in ein exakt flächengleiches Quadrat umzuwandeln (Quadratur des Kreises). Die Mathematik hat inzwischen bewiesen, daß das nicht geht. Trotzdem hat niemand Zweifel daran, das p einen ganz bestimmten Wert hat, der allerdings in Zahlenschreibweise nur mit einer gewissen Annäherung angegeben werden kann, da die Länge der Ziffernfolge ¥ ist. Je nach geforderter oder notwendiger Genauigkeit ist 3 schon ausreichend oder es wird 3,14 benutzt oder noch mehr Stellen. Das die Zahl p in sehr vielen Formeln der Mathematik eine wichtige Rolle spielt, wird nicht dadurch geändert, daß sie zunächst als das Verhältnis von Kreisumfang zu Durchmesser definiert wurde.
Für viele Kurven kann die Integralrechnung exakte Ergebnisse liefern, bei vielen Kurven ist das exakt nicht möglich. Bei einigen Kurven wurde das Integral als exakter Wert definiert (z.B. Integralsinus). In allen diesen Fällen wird eine numerische Integration durchgeführt und je nach Aufwand und Methode erhält man zwar kein exaktes, aber mehr oder weniger genaues Ergebnis, das als exakt angesehen wird.
Warum diese lange Vorrede. Der U-Wert ist ohne jeden Zweifel stationär definiert, d.h. für den Wärmestrom, der sich einstellt, wenn man die Temperaturen auf beiden Seiten der Wand lange genug konstant bleibt (Vergleich mit dem Rechteck). In der Praxis ist durch Wetter und anderes dieser Zustand (Vergleich mit einer beliebigen Kurve) natürlich nicht zu erreichen und es ist zu untersuchen wie der U-Wert dann anzuwenden ist!
Eine solche Betrachtung ist nötig, da am Bau sehr viele beteiligt sind, die unterschiedliche Fachkenntnisse und Interessen haben. Die Beteiligten sind u.a. Bauherr, Architekt, Statiker, Bauphysiker, Baustoffhersteller, Bauhandwerker. Sie müssen sich mehr oder weniger verstehen, um einen guten Bau zu errichten. Typisch dafür ist der Witz, zitiert in, [20, S. 8]: "Ein Bauingenieur ist ein Möchtegern-Architekt, der am Freihandzeichnen gescheitert ist bzw. ein Architekt ist ein Möchtegern- Bauingenieur, der in der Mathematik versagt hat". An diesem Witz ist etwas Wahres dran und trotzdem müssen sich alle verstehen. Für einen Arzt ist der bequemste Patient der, der keine Ahnung hat und alles über sich ergehen läßt. Der unbequemste Patient ist der, der etwas Ahnung von Medizin hat, aber glaubt alles zu wissen und den Arzt belehren will. Das optimale Verhältnis ist, wenn der Patient Ahnung von Medizin hat, so daß er mit dem Arzt sprechen kann, versteht, wie er behandelt wird und ggf. den Arzt auf einen Irrtum hinweisen kann. Damit ist etwa auch die Bandbreite der Beziehungen der am Bau Beteiligten gegeben.
Und nun zum eigentlichen U-Wert. Ausgangspunkt der Betrachtungen ist der Energieerhaltungssatz, der erst im 19. Jahrhundert erkannt wurde, aber heute weitgehend Allgemeingut ist. Bezogen auf die Wände ist die differentielle Formulierung (t: Zeitkoordinate, r: Ortskoordinate):
Die zeitliche Änderung des Wärmeenergieinhalts E(t,r) in einem Volumenelement ist gleich der Änderung der Wärmeströme q(t,r) zu diesem Volumenelement plus der im Innern dieses Volumenelements freigesetzten Wärmeenergie e (t,r).
Bezogen auf Wände lautet die integrale Formulierung:
Der Wärmestrom auf der einen Wandseite ist gleich dem Wärmestrom auf der anderen Wandseite verändert um die Änderung der gespeicherten Wärme der Wand und der im Innern der Wand erzeugten Wärme.
Der Begriff "verändert" in der vorliegenden Formulierung wurde gewählt, da erst nach Festlegung der Richtungen der Wärmeströme das Wort Summe oder Differenz richtig ist. Im weiteren wird vorzugsweise von der differentiellen Form ausgegangen. Im Bauwesen ist besonders darauf hinzuweisen, daß im Innern hier nicht das Innere des Gebäudes gemeint ist, sondern das Innere der Wand.
Die Dimension der Gleichung ist W/m3. Der Energiedichte in einem Stoff hat die Größe (Ws in SI-Einheiten, sonst oft Wh) Ws/m3. Durch die Differentation nach der Zeit verschwindet die Zeit (z.B. s) in der Dimension. Auch auf der anderen Seite muß diese Dimension sein. Der Wärmestrom hat die Dimension W/m2 durch Differentation nach dem Ort kommt eine Länge (z.B. m) in den Nenner hinzu also W/m3. Damit muß auch e(t, r) diese Dimension haben. Damit schließt sich z.B. automatisch die Interpretation dieses Anteils als Solarstrahlung aus, denn deren Dimension ist W/m2.
Bei der Untersuchung zum U-Wert kann aus nachfolgendem Grund der Anteil der freigesetzten Energie e (t, r) vernachlässigt werden: Es handelt sich um im Innern der Wand freigesetzte Anteile. Beispiele, wo dies berücksichtigt werden müßte, sind z.B. ein verrottender Haufen Laub, den bei der Verrottung entsteht Wärme. Ein weiteres Beispiel wäre eine teildurchsichtige Wand: Das Licht, das durch die trübe Wand scheint, wird teilweise in der Wand absorbiert und in Wärme umgesetzt. Dabei handelt es sich um eine Umwandlung der durchfallenden Strahlung (W/m2) mit einem bestimmten Betrag pro Länge (=1/m) in Wärme (W/m3) und damit stimmt die Dimension wieder. Gleiches gilt auch, wenn Mikrowellenstrahlung durchgeht, auch hier wird wieder ein Teil pro Länge in Wärme umgewandelt. Da aber bei den Wänden, die interessant sind, keiner dieser Fälle vorliegt, wird kein Fehler in der Allgemeinheit gemacht, wenn dieser Anteil unberücksichtigt bleibt. So zu verfahren ist auch aus mathematischen Gründen sinnvoll, da die Behandlung der Differentialgleichung einfacher wird, obwohl es noch kompliziert genug bleibt.
Wem beim Durcharbeiten etwas unklar bleibt, kann mich anmailen, wenn es im Rahmen bleibt, antworte ich allen. Wenn eine Frage im Bauphysikforum (http://www.bauphysik.com) gestellt wird, werde ich oder andere im allgemeinen antworten. Trotzdem rate ich dem Leser das zunächst Unverstandene als richtig anzunehmen und weiter zu lesen. Vielleicht wird dann das zunächst Unverstandene doch noch klar, oder es muß doch eine Frage gestellt werden bei der dann evtl. auch rauskommen kann, das mir ein Fehler unterlaufen ist.
In mathematischer Form ausgedrückt, nimmt der obige Energieerhaltungssatz folgende Form an (r müßte deutsche Fraktur sein, das macht mein Formeleditor aber nicht):
(1) 
Nun werden weitere Vereinfachungen getroffen, die in der Praxis oft (zumindest angenähert) erfüllt sind:
(2) E = cr
T q = l
Dabei sollen c (massenbezogene Wärmekapazität), r (Dichte) und l (Wärmeleitwert) zeit- und temperaturunabhängig und höchstens vom Ort abhängig sein. l ist im allgemeinen ein Tensor, denn der Wärmeleitwert muß nicht in allen Raumrichtungen gleich sein (z.B. bei Holz). Das bedeutet z.B., daß im allgemeinen Temperaturgradient und Wärmestrom eine etwas unterschiedliche Richtung haben. Aber in den hier betrachteten Fällen nimmt man wieder eine Vereinfachung vor, indem man den Wärmeleitwert in allen Richtungen als gleich groß annimmt und damit als eine einfache Konstante, oder nur eine Raumrichtung betrachtet. Wird die Differentiationsregel, daß bei der Differentation eines Produktes aus Konstante und Funktion die Konstante vor das Differential gezogen werden darf, beachtet geht mit (2) die Gleichung (1) über in:
(3) 
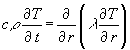
In Vektorschreibweise hat (3) folgende Form:
(4) 
Die Differentation eines Skalars nach dem Ort wird als Gradient (grad, ergibt einen Vektor) bzw. die eines Vektors als Divergenz (div, ergibt einen Skalar) bezeichnet.
Zur weiteren Auswertung wird (4) über einen Zeitabschnitt von der Zeit a bis zur Zeit b integriert:
(5) 
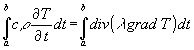
Die linke Seite von (5) ist einfach zu integrieren, da cr eine Konstante ist und die Integration eines Differentials gleich der Differenz der Funktionswerte an den Integrationsgrenzen ist. Die Integration der rechten Seite ist nicht so einfach. Die weitere Behandlung ist nur möglich, wenn Integration und div grad vertauscht werden. Das muß nicht immer zulässig sein. Indirekt ist das z.B. in [15, S. 31ff] angesprochen. In [12] und [13, S. 139 ff] wird die Vertauschung vorgenommen ohne dieses Problem zu nennen. Wird diese Vertauschung vorgenommen, wird aus (5):
(6) 
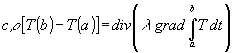
Das Integral auf der rechten Seite wird durch ein wertgleiches Produkt aus Intervalldauer und einer geeigneten Mittellwerttemperatur
ersetzt:
(7) 
Da für ein bestimmtes Zeitintervall (b a) eine Konstante ist, kann (7) durch diese Konstante dividiert werden. Da T sicher beschränkt ist, wird bei einer Zeitdauer über alle Grenzen der Bruch zu 0:
(8) 
Aus (8) ergibt sich, daß bei Zulässigkeit der Vertauschung und genügend langem Zeitintervall sich für die Mittellwerttemperaturendie gleiche Differentialgleichung wie für die stationären Verhältnisse ergibt. Da diese speziellen Voraussetzungen nicht immer gegeben sind, wird im Folgenden eine spezielle Ableitung mit weniger unbestimmten Voraussetzungen
durchgeführt.
Eine Vereinfachung von (3), die aber im folgenden selten benutzt wird, ist möglich, wenn l ortsunabhängig ist (z.B. homogene Wand):
(9) 
Für die Berechnungen muß natürlich ein räumliches Koordinatensystem benutzt werden, das der Aufgabe möglichst gut angepaßt ist. Die gebräuchlichsten Koordinatensysteme sind das kartesische (x, y, z), das zylindrische (r, j , z) und das Kugelkoordinatensystem (r, j , J ), obwohl noch weitere denkbar sind und auch teilweise benutzt werden. Für den Zweck von Wänden mit planparallen Oberflächen ist das kartesische Koordinatensystem am zweckmäßigsten. Dann wird z.B. (die e sind die Einheitsvektoren in die 3 Raumrichtungen):
(10) 
Sind die Randbedingungen usw. so, daß nur in x-Richtung eine Ortsabhängigkeit der Temperatur auftritt (isolierter Balken oder Wand), dagegen in y- und z-Richtung keine (häufigster Praxisfall und für das weitere ausreichend), sind die Ableitungen in y- und z-Richtung gleich 0 und können damit weggelassen werden. So wird aus (3):
(11) 
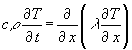
In dieser Form ist die Wärmeleitungsgleichung vielen bekannt (z.B. Fouriersche Dgl.) und akzeptiert. Eine andere Form von (11) ist:
(12) 
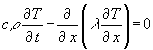
(11) ist eine lineare partielle Differentialgleichung. Um das zu beweisen, wird die Temperatur als eine Summe von Teiltemperaturen angesetzt:
(13) T = T1 + T2 + T3
Nach den Regeln zur Differentation von Summen (die Differentation einer Summe ist gleich der Summe der einzelnen Differentationen) wird mit (13) aus (11):
(14) 
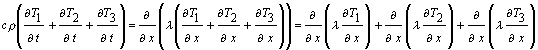
Zur weiteren Behandlung setze ich für T in (11) nacheinander die Teillösungen T1, T2 und T3 (von denen nur vorausgesetzt wird, das sie existieren) ein und erhalte 3 Dgl.:
(15) 
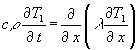
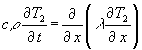
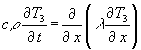
Werden die 3 Gleichungen (15) addiert, so wird (14) erhalten, womit die Linearität bewiesen ist.
Zur Lösung von (11) reichen die Angaben noch nicht aus. Da 3 Differentationen (1 nach der Zeit und 2 nach dem Ort) sind, sind noch 3 Bedingungen anzugeben, die als Rand- und/oder Anfangsbedingungen bezeichnet werden. Siehe dazu [1], [4, S. 8ff], [5] und [6]. Gewählt werden hier 2 Randbedingungen und zwar den Temperaturzeitverlauf auf der Außenseite der Wand, auf der Innenseite der Wand und als Anfangsbedingung den Temperaturverlauf von der Außenseite zur Innenseite zum Anfangszeitpunkt. Jede andere Wahl, z.B. statt des Temperaturzeitverlaufs auf der Außenseite der Wand den Wärmestromzeitverlauf auf der Außenseite der Wand würde zwar eine andere Art des Lösungsweges bringen, aber wenn reale Verhältnisse beschrieben werden sollen, sind die Lösungen doch gleich. Mehr als 3 Bedingungen sind sinnlos, denn dann werden Forderungen gestellt, die die mathematische Gleichung nicht zuläßt und die in der Praxis Unsinn sind.
Zur Vereinfachung der Lösung teile ich die Bedingungen auf. T1 soll die Randbedingung an der Außenwand erfüllen und an der Innenwand gleich 0 sein, T2 soll die Randbedingung an der Innenwand erfüllen und an der Außenwand gleich 0 sein, T3 soll den Anteil aus dem Anfangstemperaturverlauf in der Wand repräsentieren. Wenn genügend lange Zeit vergangen ist, wird wegen der Wärmeabstrahlung dieser Anteil zu Null werden. Das folgt aus der Überlegung das nach genügend langer Zeit der Temperaturverlauf in der Wand nicht mehr von dem Anfangstemperaturverlauf abhängen kann und mathematisch z.B. in der Form, daß in [3, S. 556, Gl. (39)] beim Wachsen der Zeit t über alle Grenzen
(16) 
wird.
Deshalb ist nach genügend langer Zeit die Lösung T3 unwichtig, wird zu 0 gesetzt und deshalb nicht weiter untersucht.
Es ist anzunehmen, daß die Temperatur irgendwann und irgendwo in der Wand von den Anfangs- und Randbedingungen abhängt. Die weitere Rechnung wird zeigen, daß dem auch so ist.
Da wegen der Linearität, wie schon erwähnt wurde, die 3 Bedingungen (je eine Randbedingung für jede Seite der Wand und die Anfangsbedingung Temperaturverteilung in der Wand zu Beginn) je einer Teillösung zugewiesen werden können, ist es beweismäßig am einfachsten, das zu tun. Die Lösung, die die Anfangsbedingung erfüllt, wird (wie auch schon erwähnt) nicht weiter untersucht, da diese Lösung in der Praxis nach wenigen Tagen abgeklungen ist und damit für die Temperaturverteilung in der Wand zu späteren Zeiten unwesentlich ist. Die Herleitung der beiden anderen Lösungen sind äquivalent, nur wird einmal von x = 0, das andere mal von x = w ausgegangen. Es reicht deshalb, eine Lösung zu untersuchen. Gewählt wird die Lösung, die von x = 0 ausgeht und in Abschnitt 2.3 als T1 bezeichnet wurde. Da es sich aber auch um das Beispielvorgehen handelt, wird der Index 1 weggelassen.
Für diese Einzellösung der Temperaturverteilung in der Wand ist folglich nur die Randbedingung (d.h. der zeitliche Temperaturverlauf) an der Wandoberfläche bei x = 0 verantwortlich, d.h. zu irgendeinem Zeitpunkt sollte die Temperatur an irgendeiner Stelle der Wand nur von dem Temperaturverlauf an der Wandoberfläche der Vergangenheit abhängen.
Mit dieser Annahme erscheint ein Integralansatz zweckmäßig (im weiteren Rechengang zeigt sich, daß das tatsächlich weiterführt), der die Randbedingung T(t, 0) mit einer noch zu bestimmenden Funktion G(t , x) faltet, wobei t die Vergangenheit mit der Dimension einer Zeit ist.
Aus diesen Überlegungen erscheint folgender Ansatz für die Lösung der Dgl. (12) zweckmäßig:
(17) 
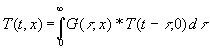
Das Integral hat verschiedene Namen (in [6] z.B. Duhamelsches Theorem), die Funktion G hat die Namen Gewichtsfunktion, Greensche Funktion usw. und hat die Dimension 1/s. In Gleichung (17) ist die Faltungsform für das Integral gewählt. Gleichwertig wäre auch folgender Ansatz:
(18) 
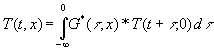
Die Funktion G*(t , x) unterscheidet sich dadurch von G(t , x), daß die Werte statt für t ³ 0 für t £ 0 bestimmt werden müssen. Beide Funktionen müssen für 0 £ x £ w bestimmt werden. Im weiteren wird mit (17) weiter gerechnet, da die Faltungsform der Anwendung der Laplacetransformation in anderen Fällen entgegenkommt.
Zur weiteren Bearbeitung wird (17) nach der Zeit differenziert (da t nicht als Integrationsvariable auftritt, darf der Integrand differenziert werden):
(19) 
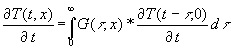
Auf der rechten Seite von (19) tritt t nur in der Differenz t - t auf, deswegen liefert die Differentation nach t oder t dasselbe, nur mit umgekehrten Vorzeichen. Deshalb kann (19) die rechte Seite durch partielle Integration umgeformt werden:
(20)
Die eckige Klammer in (20) ist 0, wie sich später noch ergeben wird: weil G(t , x) für t = - ¥ oder 0 gleich 0 ist. Wird (17) und (20) in (11) eingesetzt, ergibt sich:
(21) 
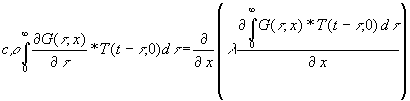
Mit der zulässigen Vertauschung von Integration und Differentation, die in praktischen Fällen immer zulässig ist (bei mathematischen Spezialfällen muß die Zulässigkeit nachgewiesen werden) und Umordnung, wird aus (21):
(22) 
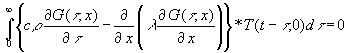
Damit (22) für beliebige T(t) erfüllt wird, muß der Wert der geschweiften Klammer identisch 0 sein:
(23) 
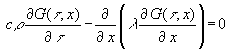
Die Gleichung (23) ist formal derselbe wie (11), nun aber für G statt T. Als Randbedingung gilt hier:
(24) G(t , 0) = d (t ) (Deltafunktion, ist überall 0 außer für t = 0),
(25) G(0, x) = 0 und G(t , w) = 0 (w: Wandbreite).
Die Randbedingungen (24) und (25) scheinen sich bei G(0, 0) zu widersprechen, aber das ist eine Frage der Annäherung, ob man von x oder von t zu diesem Punkt kommt, bei Grenzübergängen ist das manchmal zu berücksichtigen.
Außerdem ergeben sich aus (17) noch Kenntnisse über G(t ,x). Wird für T(t,0) eine sehr kurze, aber heiße Temperaturspitze zur Zeit t = 0 (theoretisch eine d -Funktion) mit dem Integral T0 gewählt:
(26) T0 =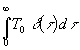 
= 
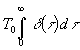
wird aus (17) entsprechend den Rechenregeln mit d -Funktionen:
(27) 
= 
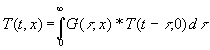Aus den Gesetzen der Wärmelehre, die ja auch durch die Wärmeleitungsgleichung untermauert werden, ergibt sich, daß
(28) G(t , x) ³ 0
sein muß, da ja ein Temperaturunterschied höchstens verkleinert, aber nicht vergrößert werden kann. Z.B. bedeutet das, das bei positiven T0 die Temperatur T(t, x) nie negativ werden kann. Daraus folgt auch, daß
(29) 
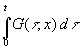= monoton steigend bei wachsenden t
Außerdem ergibt sich aus (17) und (28) noch der Wert von G(¥ ,x). Dazu wird (17) bei einer zeitunabhängigen Temperatur betrachtet. Diese zeitunabhängige Temperatur kann vor das Integral gezogen werden. Damit wird:
(30) 
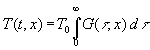
Da T0 nicht überschritten werden kann, gilt auch:
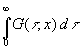(31) 
£
1
Eine Konsequenz von(29) und (31) ist, daß G(t , x) einen Grenzwert haben muß:
(32) 
= 0
Denn würde (28) aber nicht (32) gelten, könnte (31) nicht erfüllt werden.
Für den Spezialfall w ® ¥ und l , cr konstant ist eine geschlossene Lösung für (22) bekannt:
(33) 
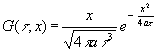mit 
Diese Funktion erfüllt alle Bedingungen: Für x = 0 ist G = 0, für t ® ¥ ist G ebenfalls 0 und in bei einem beliebig kleinen Bereich von x ist für t beliebig klein der Wert von G beliebig groß und das Integral über den ganzen Bereich = 1.
Für w endlich und l , cr ortsabhängig ist dem Autor keine geschlossene Lösung bekannt. Für l , cr konstant ist eine numerische Lösung durch Ausnutzung von Symmetrieeigenschaften relativ einfach zu erhalten [18]. Für den allgemeinen Fall ist der numerische Aufwand höher. Für das weitere reicht es aber zu wissen, das eine Lösung existiert. Für praktische Fälle reicht schon die Anschauung dafür, das die Lösung existiert. Für Mathematiker gehört dazu, das Existenz und Eindeutigkeit der Lösung bewiesen werden. Das aber hat die Mathematik in der Theorie der partiellen linearen Differentialgleichungen schon bewiesen. Speziell für die Wärmeleitungsgleichung z.B. in [14, S. 302]. Deshalb wird im weiteren davon ausgegangen, daß diese eindeutige Lösung existiert.
Die Lösung für T2 erhält man durch eine analoge Herleitung. Damit ist eindeutig bewiesen, das der zeitliche und örtliche Temperaturverlauf in der Wand zu erhalten ist (allerdings mit ggf. größerem mathematischen Aufwand), wenn nur die Oberflächentemperaturen beider Wandseiten über eine genügend lange Zeit bekannt sind. Ausdrücklich sei darauf hingewiesen, daß es sich um die Oberflächentemperaturen der Wand und nicht um die Umgebungstemperaturen handelt.
Besonders interessant ist der Wärmestrom. Dieser ergibt sich aus Temperaturgradient und Wärmeleitwert l (siehe (2)). Den Temperaturgradienten erhält man, in dem man (17) nach x differenziert. Da nur G(t , x) das x enthält, kann unter dem Integralzeichen differenziert werden und man erhält:
(34) 
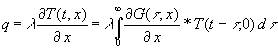
Will man den Wärmestrom auf der Seite des Temperaturverlaufs haben, ist die Ableitung von G an der Stelle x = 0 zu nehmen. Will man den Wärmestrom auf der anderen Wandseite haben, so ist die Ableitung von G an der Stelle x = w zu nehmen. Für den Gesamtwärmestrom sind natürlich genau wie bei der Temperatur die beiden Teillösungen für T1 und T2 zu addieren.
Durch (17) ist der Temperaturverlauf in der Wand gegeben. Gemäß (2) ist dann auch die Energiedichte gegeben. Wird über die ganze Wand integriert, wird die gespeicherte Wärmeenergie erhalten:
(35) Ew(t) =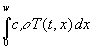 
= 
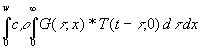
Hier ist auch die Vertauschung der Integrationsreihenfolge zulässig. Damit wird:
(36) Ew(t) =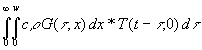 
Dazu ist (36) nach der Zeit zu differenzieren. Da nur T zeitabhängig ist, ist die Vertauschung der Reihenfolge von Differentation und Integration zulässig:
(37) 
= 
= 
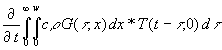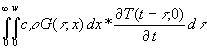
Da in (37) t nur in der Differenz mit t auftritt, darf die Differentation nach t durch die Differentation nach t ersetzt werden (Vorzeichen von t beachten):
(38) = 
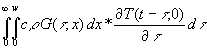
Mit partieller Integration kann (38) weiter ausgewertet werden:
(39) = 
+ 
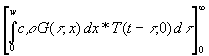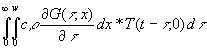
Der Wert der eckigen Klammer ist 0 wegen (25) und (32). Im rechten Term kann man mit (23) die Differentation nach t durch eine nach x ersetzen:
(40) = 
= 
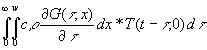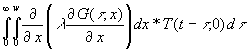
Die Integration des inneren Integrals ist jetzt einfach auszuführen, indem die Differentation wegfällt:
(41) = 
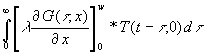
oder mit Trennung der eckigen Klammer:
(42) 
= 
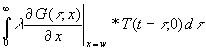
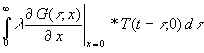
Das Ergebnis ist keine Überraschung, denn das ist die integrale Formulierung des Energieerhaltungssatzes am Anfang Abschnitt 2. Gleichzeitig ist damit der Zusammenhang zwischen differentialer und integraler Formulierung des Energieerhaltungssatzes bewiesen.
Interessant ist die Heizleistung auf der Wandinnenseite, also bei x = w. Dafür wird aus (42) der Term genommen, der diese Leistung beschreibt:
(43) Nw(t) =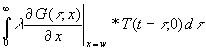
Um die Heizenergie Q12 für einen Zeitabschnitt zu erhalten wird (43) von t1 bis t2 integriert:
(44) Q12 =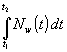 
=
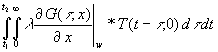
Das Doppelintegral kann durch Vertauschung der Integrationsreihenfolge von t und t (hier wieder zulässig) und Berücksichtigung, das G(t , x) nicht von t abhängig ist, folgend umgeformt werden:
(45) Q12 =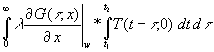
In vorstehender Gleichung wird für t t = t* eine Variablensubstitution durchgeführt. Damit wird:
(46) Q12 =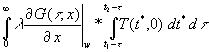
Die Integrale mit t1 und t2 spalte ich bezüglich der Integrationsgrenzen auf:
(47) 
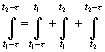
Mit (47) wird aus (46), wenn man gleichzeitig die Integrationsvariable t* in t umbenennt (auf den Namen kommt es ja nicht an):
(48) Q12 =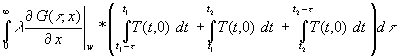 
Hier sind weitere Umformungen zweckmäßig. Das mittlere Integral in der runden Klammer enthält t nicht mehr und kann deshalb als Konstante (bezüglich t ) vor das Integral über t gezogen werden. Im letzten Integral ist die Vertauschung der Integrationsgrenzen zweckmäßig. Damit wird:
(49) Q12 =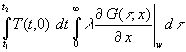 
+
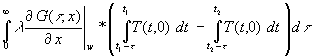
Das Integral über t im ersten Summanden ist von t unabhängig und muß deshalb eine material- und/oder wandabhängige Konstante sein. Betrachtet man stationäre Verhältnisse, d.h. einen Zeitraum nach sehr lange konstant bleibender Temperatur, so ist der 2. Summand = 0, da der Ausdruck in der runden Klammer als Differenz gleicher Größen zu 0 wird. Da das Integral über t im ersten Summanden von (48) den Wärmestrom bei beliebigen instationären Verhältnissen bestimmt, muß dieses Integral auch bei dem Spezialfall der instationären Verhältnisse, den stationären Verhältnissen gelten. Deshalb ist ein Vergleich mit der Definition des U-Wertes in der DIN mit stationären Verhältnissen sinnvoll.
Die Gleichung (3) der DIN 4108 Teil 5 08/81 lautet (in der DIN steht noch k statt U):
Nach den Voraussetzungen dieser Abhandlung wird nur L berechnet. Entsprechend Abschnitt 0 wird im weiteren L so wie U behandelt, da nur in diesem Anteil von der kompletten U-Definition auch die Speicherwirkung zu berücksichtigen ist.
Wegen der Definition des U-Wertes bei stationären Verhältnissen und der Konstanz des Integral über t im ersten Summanden von (49) muß gelten:
(50) 
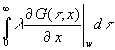= U
Das bedeutet, daß folgende Identität existieren muß und auch existiert (78):
(51) 
= 
Mit (50) wird aus (49):
(52) Q12 =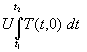 
+
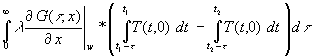
Zur weiteren Auswertung von (52) wird eine Zwischenrechnung ausgeführt, indem (23) einmal über x integriert wird. Damit folgt aus (23):
(53) 
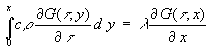
Mit (53) wird aus (52):
(54) Q12 = +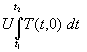
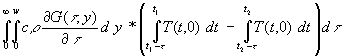
Durch partielle Integration kann das Doppelintegral umgeformt werden. Da wieder die Vertauschung von Integration und Differentation zulässig ist, kann der Integrand selbst integriert werden. Bei der Differentation der Integrale in den runden Klammern muß beachtet werden, das vor der Differentation die Integrationsgrenzen getauscht werden müssen (Vorzeichenwechsel):
(55) =
+
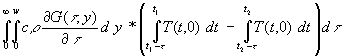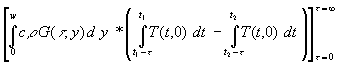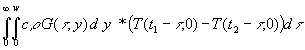
Der Term mit den eckigen Klammern ist 0, weil bei t = 0 bei den Integralen in den runden Klammern obere und untere Integrationsgrenze gleich sind Þ Integralwert = 0 und bei der oberen Integrationsgrenze nach (32) G(¥ ,y) º 0 ist. Mit (55) wird aus (54):
(56) Q12 = +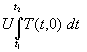 
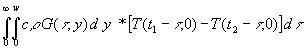
Wird (56) mit (36) verglichen, so stellt man fest, das das Doppelintegral genau die Änderung der in der Wand gespeicherten Wärmeenergie vom Anfangszeitpunkt (t1) und zum Endzeitpunkt (t2) ist.
Je nachdem wie groß das Speichervermögen der Wand, die Temperaturänderungen und/oder die Zeitdauer t2 t1 ist, kann die Änderung der gespeicherten Energie größer sein als die Heizenergie durch stationären Wärmedurchgang. Z.B. kann ohne weiteres bei einer stark speicherfähigen Wand die Energieeinspeicherung durch den Außenwandtemperaturanstieg infolge Sonnenstrahlung bedeutend größer als der tägliche Heizenergiebedarf sein. Wird aber eine bedeutend längere Heizperiode betrachtet, ist die Ungenauigkeit des Heizenergiebedarfs infolge der Instationarität (Änderung der gespeicherten Wärmeenergie) zu vernachlässigen. Dabei ist das erste Integral in (56)
(57) 
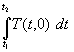= Gradtagszahl oder äquivalente Größe.
Durch die Speicherwirkung der Wand ist der Wärmestrom auf der Innenseite der Wand natürlich nicht von der Augenblickstemperatur auf der Außenseite der Wand bestimmt, sondern von den Temperaturen vorher, gewichtet mit der Ableitung der Gewichtsfunktion G. Damit zeigt sich, das der U-Wert aus Augenblickswerten bei beliebigen Temperaturzeitverlauf nicht bestimmt werden kann. Anders sieht es bei langen Zeiten aus.
Hierzu wird (34) über eine gewisse Zeitspanne von t1 bis t2 integriert:
(58) 
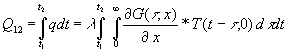
Da t nur in T(t - t , 0) vorkommt, ist eine Vertauschung der Integrationsreihenfolge zulässig:
(59) 
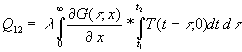
In dem inneren Integral wird eine Variablensubstitution t - t = z vorgenommen. Damit wird aus (59):
(60) 
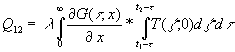
Ein Integrationsbereich kann in mehrere Integrationsbereiche aufgeteilt werden. Gewählt wird hier auch die Aufteilung (47). Das mittlere Integral enthält t nicht mehr und stellt im Sinne der Integration bezüglich t eine Konstante dar und kann vor das Integral gezogen werden. Für die anderen beiden Integrale sind Abschätzungen möglich. Dazu wird der Mittelwertsatz der Integralrechnung [2, S. 189ff] benutzt:
(61) 
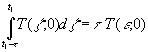mit t1 - t £ e £ t1
Der Wert T(e,0) liegt mit Sicherheit zwischen der höchsten und tiefsten Temperatur, die irgendwann mindestens einmal auftreten. Nehme ich statt T(e,0) die höchste bzw. tiefste Temperatur, wird der exakte Wert entweder vergrößert oder verkleinert. Zur weiteren Herleitung bezeichne ich T(e,0) mit , der Wert wird dann später wieder mit der höchsten oder tiefsten Temperatur identifiziert. Dieser Wert ist unabhängig von t und in diesem Sinne eine Konstante und kann auch wieder vor das Integral gezogen werden. Aus (60) wird dann mit (47) und (61) und folgende Gleichung (bei t2 ist die entgegengesetzte Richtung des Intervalls zu t1 zu beachten, deswegen das negative Vorzeichen):
(62) 
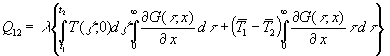
Die Integrale über t interessieren an der Stelle x = w und sind feste Werte, die unabhängig vom Temperaturverlauf sind. Ich bezeichne sie mit K1 bzw. K2:
(63) 
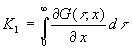bzw.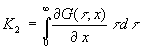 
Mit (63) wird aus (62):
(64) 
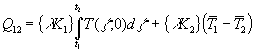
Für Q12 setze ich wieder die Definition aus (58) ein:
(65) 
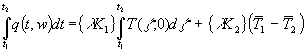
Zur Auswertung von (65) soll während einer sehr langen Zeit eine konstante Temperatur TK anliegen. So ist die minimale Temperatur gleich der maximalen gleich TK. D.h.
und auch 
sind gleich TK. Damit ist auch der Wärmestrom q(t,w) konstant, d.h. zeitunabhängig = qK. Die Integration einer Konstante (hier qK und TK) liefert als Ergebnis das Produkt von Konstante und Intervallgröße. Damit wird:
(66) 
Dividiert man (66) durch die Zeitdauer ergibt sich:
(67) 
Vergleicht man (67) mit der Festlegung des U-Wertes:
(68) 
so sieht man sofort, das:
(69) 
ist.
Mit (69) wird aus (65):
(70) Q12 =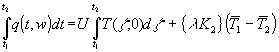 
In (70) ist noch der letzte Term zu interpretieren. Dazu ein Gedankenexperiment: bis zur Zeit t1 habe ganz lange eine untere Temperatur Tu geherrscht, so daß sich in der Wand der Beharrungszustand ausgebildet hat. Danach wird die Temperatur beliebig erhöht und vermindert, ohne aber eine obere Temperatur To zu überschreiten bzw. Tu zu unterschreiten. Zum Schluß wird die Temperatur auf der oberen Temperatur To konstant gehalten, bis wieder der Beharrungszustand zur Zeit t2 erreicht ist. Um den letzten Term in (70) extrem zu machen, wird beispielsweise mit Tu identifiziert undbeispielsweise mit To identifiziert (siehe Absatz nach (61). Damit ist der Wert (-) gleich To - Tu oder Tu To. Größere Extremwerte kann (-) nicht annehmen. Was hat sich aber in der Wand geändert? Im Beharrungszustand Tu war in der Wand eine bestimmte Wärmeenergie gespeichert. Im Beharrungszustand To ist in der Wand eine größere Wärmeenergie gespeichert. Diese Differenz der gespeicherten Energien ist aber proportional zu der Differenz To - Tu. Damit ist auch l
K2 identifiziert: es ist die Konstante des Speichervermögens S der Wand. Damit wird aus (70):
(71) 
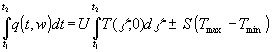
Mit Tmax bzw. Tmin sind die maximalen bzw. minimalen Temperaturen während und vor (bis etwa der Dauer einiger Speicherzeitkonstanten der Wand) des gemessenen Zeitintervalls gemeint. Der letzte Term von (71) hat eine beschränkte Größe, dagegen ist die gesamte geflossene Wärmemenge über einen sehr langen Zeitraum (mindestens ein Vielfaches der Speicherzeitkonstante) beliebig groß, so daß in der Bilanz die Speicherwirkung nur eine untergeordnete Rolle spielt. Die Größe
ist je nach Maßeinheit z.B. die Gradtagszahl. Daraus folgt, daß bei genügend langer Zeit der U-Wert die gleiche Rolle spielt wie im stationären Zustand, bei dem er definiert wurde.
Das habe ich bereits in Kurzfassung in [16] und [17] dargelegt.
In (50) wurde auf den U-Wert hingewiesen. Es hatte sich in der Herleitung von (49) gezeigt, das allein aus der Tatsache, daß eine Lösung der Wärmeleitungsgleichung (11) existiert automatisch eine aufbau- und/oder materialabhängige Konstante resultiert. Würde die Lösung bekannt sein, könnte das Integral (50) direkt ausgerechnet werden. Da aber keine allgemeine Lösung bekannt ist, muß ein anderer Weg gegangen werden. Die Existenz dieser Konstante war für den allgemeinen stationären Fall bewiesen worden. Da stationäre Verhältnisse "nur" ein Sonderfall der instationären Verhältnisse sind, muß diese Konstante auch bei stationären Verhältnissen gelten. Im Text nach (49) wurde gesagt, das bei stationären Verhältnissen der letzte Summand gleich 0 ist. Das soll nachfolgend bewiesen werden.
Dazu wird zuerst der Integrationsbereich über t in einen Bereich unterhalb einer beliebig wählbaren Zeit t 3 und einer Zeit darüber aufgeteilt:
(72) 
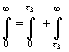
Ab der Zeit t1 t 3 soll eine konstante Temperatur beispielsweise T3 herrschen. Damit wird aus dem letzten Term von (49):
(73) =
+
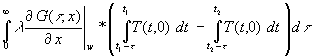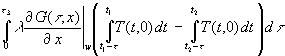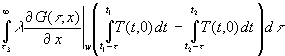
Die runde Klammer im 1. Summanden ist = 0 weil die sich die Integrale in der Klammer leicht lösen lassen. Nach Voraussetzung ist zu allen Zeiten t von t1 t 3 bis t2 die Temperatur T(t,0) konstant = T3. Damit ist über eine Konstante zu integrieren und das Ergebnis ist T3t . Da beide Integrale den gleichen Wert haben, ist ihre Differenz natürlich 0.
Beim 2. Summanden wird 
betrachtet. In diesem Ausdruck hat t
nur Werte > t
3. Wenn t
3 groß genug ist, ist << 1 und für t
3 ®
¥
sogar Null. Das ist eine Folgerung aus (32), denn wenn
(74) 
= 0
nicht gelten würde, wäre (32) nicht möglich. Im Theoretischen müßte t 3 tatsächlich den Wert ¥ annehmen, im praktischen Versuch wählt man t 3 so groß, daß sich die Meßwerte bei weiterer Vergrößerung nicht mehr wesentlich ändern. Das ist z.B. der Fall wenn die Meßungenauigkeit > als die Änderung wird. Damit ist auch dieser 2. Summand bei hinreichend großen t 3 gleich 0. Was zu beweisen war.
Wenn in (11) nun die stationäre Lösung betrachtet wird, ist T = konstant. Damit ist automatisch die Ableitung der konstanten Temperatur nach der Zeit = 0, d.h. die linke Seite von (11) ist 0. Dann muß aber auch die rechte Seite von (11) gleich Null sein. Das ist nur möglich, wenn der Ausdruck in der Klammer eine Konstante (z.B. C) ist. Und zwar der konstante Wärmestrom der durch die Wand fließt, entsprechend der Definition von l . Damit ist entsprechend der Definition für U-Wert für C anzusetzen (D T: Temperaturdifferenz über der Wand):
( 75) C = U D T
Damit (und der erwähnten 0-Setzung der linken Seite) wird aus (11):
(76) 
= C Þ
= 
Þ
= 
Mit der Integration von (76), am Besten über die ganze Wandbreite wird:
(77) 
= 
= 
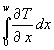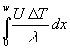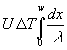
Das erste Integral ist ganz einfach zu lösen. Da das Differential der Temperatur zu integrieren ist, ist das Ergebnis ganz einfach die Temperaturdifferenz DT. Dadurch kann D T gekürzt werden. Nach Division durch U erhält man:
(78) = 
In der Praxis ist l stückweise stetig (Schichtenaufbau verschiedener Materialien) und das Integral geht in die Summenformel zur U-Wert-Bestimmung über [10, Formel (2)].
Auch der Grenzwert eines weiteren Integrals kann angegeben. Im stationären Zustand , d.h. während einer theoretisch ¥ langen Zeit, ist in (36) die Temperaturfunktion T(t t , 0) eine Konstante (beispielsweise T4), die als Konstante vor das Integral gezogen werden kann. Aus (36) folgt dann:
(79) Ew(t) =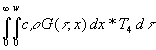 
= 
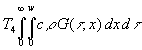
In (79) ist wieder das Integral nicht allgemein zu bestimmen. Man geht deshalb von (35) aus. Die Funktion T(t, x) ist im stationären Zustand zwar nicht mehr zeitabhängig, aber trotzdem x-abhängig. Auf der Seite x = w soll ja die Temperatur gleich 0 sein (entsprechend dem Ansatz in Abschnitt 2.4), auf der Seite x = 0 soll die Temperatur T4 sein. Wenn in (77) wird statt des Integrationsbereichs 0 bis w der Bereich x bis w genommen. Da x als Integrationsgrenze auftritt wird die Integrationsvariable y genannt. So entsteht aus (77):
(80) T(x) =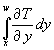
= 
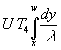
Mit (78) ist klar, das der stationäre Temperaturverlauf richtig beschrieben wird. T(w) muß nach Voraussetzung 0 sein und ist es auch, da untere und obere Grenze identisch sind. Für x = 0 ist das Integral = 1/U, U kann gekürzt und T(0) ist = T4 wie vorausgesetzt. Damit wird aus (35) und einer Speicherkonstante S (Dimension Ws/K):
(81) Ew(T4) = S T4 = =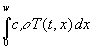 
= 
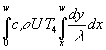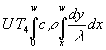
Durch Kürzen wird daraus:
(82) S =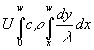 
~
wenn cr
und l
konstant sind.
Der Rechenweg für diesen speziellen Wert ist folgender: die Konstanten können vor die Integrale gezogen werden. Das verbleibende Doppelintegral liefert dann w2/2 und w/l ist 1/U. In der Praxis sind bei geschichteten Wänden die Werte stückweise konstant. Damit sind keine Integrale zu lösen.
Gleichung (11) ist eine lineare Differentialgleichung. Auch die Reaktion der Oberflächentemperatur auf Änderung von Umgebungstemperatur oder Strahlungseinflüssen ist weitgehend linear. Sogar der Strahlungsaustausch nach dem Stefan-Boltzmannschen Gesetz ist in erster Näherung linear (trotz 4. Potenz der absoluten Temperatur).
Dazu ist davon auszugehen, daß bei Temperaturgleichheit (z.B. bei einer Temperatur Tu) sich keine Temperaturen trotz starken Strahlungsaustauschs ändern können sonst wäre es ja keine Temperaturgleichheit. Würde irgendeine Oberfläche stärker strahlen, würde irgendeine andere Oberfläche mehr Strahlung empfangen, als sie selbst abgibt. Damit würde von selbst ein Temperaturgefälle entstehen, aus dem Energie gewonnen werden könnte: ein Perpetuum Mobile. Aber natürlich erhöht sich die Strahlungsabgabe E einer Oberfläche, wenn deren Temperatur erhöht wird (z.B. um DT), es ist aber "nur" der Strahlungsanteil DE zu ermitteln, um den sich die Strahlung gegenüber der Gleichgewichtsstrahlung erhöht. Dazu ist von der erhöhten Strahlung infolge der höheren Temperatur die Strahlung abzuziehen, die genau wie bei der Gleichgewichtstemperatur weiterhin empfangen wird. Denn im Gleichgewicht waren ja beide Strahlungsteile (der empfangene und der abgestrahlte) gleich. Denn sonst, d.h. wenn es nicht so wäre, wäre es ja kein Gleichgewicht gewesen. Formelmäßig sieht das so aus:
( 83) DE = s (T + DT)4 s T4 = s [(T4 + 4 T3DT + 6 T2DT2 + 4 TDT3 + DT4) T4]
Umgeformt wird daraus:
( 84) DE = s 4 T3DT [1+ 
+ 
+ 
]
Wenn DT << T bleibt (und das ist praktisch meistens erfüllt) weicht der Wert der eckigen Klammer nur unwesentlich von 1 ab und diese Abweichung ist zu vernachlässigen. Damit ist der zusätzliche Strahlungsanteil proportional der Temperaturdifferenz, d.h. auch hier herrscht Linearität.
Wenn Linearität vorausgesetzt wird, pflanzt sich eine harmonische Erregung (z.B. eine sinusförmige) auch harmonisch fort. Das bedeutet, wenn man die Folgen der Erregung irgendwo betrachtet, tritt auch dort eine harmonische Reaktion auf allerdings mit (im Allgemeinen) veränderter Amplitude und ggf. Verzögerung. Infolge der Linearität ist außerdem die Gesamtreaktion von einzelnen harmonischen Vorgängen die Summe der einzelnen harmonischen Vorgänge.
Der Beweis dafür ist z.B. in der Nachrichtentechnik gang und gäbe. Da wird jedes Element (z.B. entsprechend einer Wandschicht) als Vierpol beschrieben. Diese Vierpolverhalten ist z.B. auch von [7] für jede Schicht berechnet worden, ebenso wie die Verknüpfung der einzelnen Schichten zum Gesamtsystem.
Da der Mittelwert (über eine Periode) jedes harmonischen Vorgangs º 0 ist und jede periodische Erscheinung in eine Summe harmonischer Vorgänge zerlegt werden kann, kann kein zusätzlicher periodischer Vorgang (z.B. Sonnenstrahlung) unabhängig von den Eigenschaften der Vierpole (z.B. ob speicherarm oder speicherreich) die Heizenergiebilanz verändern. Dazu muß noch einmal betont werden, daß das nur bei Zutreffen der Linearität gilt. Allerdings muß bei einer speicherarmen Konstruktion die maximal verfügbare Heizleistung größer als bei einer speicherreichen Konstruktion sein, da wegen der geringeren Amplitudenabschwächung die erforderlichen Heizleistungsspitzen größer sind. Das berücksichtigt auch die DIN 4701.
Bis jetzt ist noch nichts über die Periodendauer (und das war auch nicht nötig) gesagt worden. Die Aussagen gelten, ob die Periodendauer nun 1 Stunde, 1 Tag, 1 Jahr oder mehrere Jahre ist. Aber wird nun mancher Leser einwänden, das stimmt ja beim Heizenergieverbrauch nicht, denn er hat nicht an die Linearitätsvoraussetzung gedacht. Die Heizung ist nämlich kein lineares System. Solange Heizleistung gebraucht wird, ist die Heizleistung der geforderte Wärmestrom. Wenn es aber draußen wärmer wird, kehrt irgendwann der benötigte Wärmestrom sein Vorzeichen kurzzeitig oder längerfristig (Sommer) um die Heizung kann das aber nicht. Wenn das umgedrehte Vorzeichen bedient werden soll, wird eine Kühlung gebraucht und die braucht auch Energie (Wärmepumpe). Damit ist die Bedingung Linearität nicht mehr erfüllt. Eine Linearität würde erfordern, das bei gleichem längerfristigem Temperaturanstieg immer die gleiche Heizleistungsreduzierung erfolgen müßte, aber die Heizleistung unter 0 zu reduzieren geht nicht.
Zu dieser Nichtlinearität kommen noch weitere technische Nichtlinearitäten: die Temperatur- und Feuchteabhängigkeit der "Konstanten" c, r und l der Wärmeleitungsgleichung.
Eine weitere Nichtlinearität ist der Nutzer. Je nachdem wie er sich behaglich fühlt, stellt er am Heizungsregler eine höhere oder niedrigere Temperatur ein. Welche Faktoren für die Behaglichkeit wichtig sind, ist zwar im Großen und Ganzen bekannt, hat aber im Einzelnen einen gewissen Spielraum.
Im Bereich der Heizgrenze steigt die Tagesmitteltemperatur mit ca. 0,5 K/Tag. Realistisch ist auch eine Tag- Nachtschwankung zum Tagesmittelwert von ca. ± 5 K. Bei einer speicherarmen Wand ist dann schon etwa 10 Tage eher zeitweise zu heizen (5 K/(0,5 K/d)) als bei einer speicherreichen Wand, aber etwa auch noch 10 Tage später ist die Heizung zeitweise abzuschalten, d.h. die Übergangszeit dauert 20 Tage. Wird der Wärmeüberschuß in der heizfreien Zeit immer weggelüftet, so ist die weggelüftete Wärme durch Heizen zu ersetzen. Früherer Heizbeginn und Mehrverbrauch ergänzen sich, darum ist die zusätzliche Gradtagszahl etwa 5 K * 10 d = 50 Kd. Beim Ende der Heizperiode ist noch einmal der gleiche Übergang mit etwa 50 Kd. Dadurch erhöht sich der Transmissionswärmebedarf wegen der etwa 3500 Kd der Heizperiode nur um ca. 2,9 % (100 Kd / 3500 Kd). Der Mehrbedarf bei der Heizenergie kann größer sein wegen der kleinen Differenz großer Zahlen.
Zwar sei noch einmal ausdrücklich darauf hingewiesen, daß es sich in dieser Abhandlung hauptsächlich um die Oberflächentemperaturen der Wand und nicht um die Umgebungstemperaturen handelt. Dieser Teil ist nur kurz in Abschnitt 7 gestreift. Für die Temperaturen der Oberfläche ist dabei nicht nur die Solarstrahlung zu berücksichtigen, die tagsüber zu Wandtemperaturen über der Umgebungstemperatur führt, sondern auch die Abstrahlung nachts, wodurch die Temperatur der Wand unter der Umgebungstemperatur liegen kann. Für diese Einflüsse ist in [8] die Sonnentemperatur benutzt, wird aber auch kritisiert. In einem Auszug aus [11] sind einige Formeln zur Umgebungstemperaturkorrektur aufgeführt. Für evtl. Korrekturen des Wämeflusses durch die Wand bezogen auf die Umgebungstemperatur ist das Integral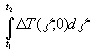 
zu ermitteln, wobei D
T die Differenz zwischen Umgebungstemperatur und Sonnentemperatur ist. t1 und t2 könnten z.B. Anfang und Ende der Heizperiode sein. Ist dieses Integral klein gegenüber der Gradtagszahl der Umgebungstemperatur, ist auch der Strahlungsgewinn nicht hoch.
Aber der Hauptteil der Arbeit hat noch etwas gezeigt: man muß keine Temperaturen im Wandinnern messen, um die gespeicherte Wärmemenge zu bestimmen. Wenn man aus den Wandinnentemperaturen die gespeicherte Wärmemenge berechnen will, muß man sich auf die angegebenen Konstanten c und r verlassen. Um die gespeicherte Wärmemenge aus dem Verlauf der Oberflächentemperaturen zu berechnen, braucht man noch zusätzlich l . Aber l ist meist genauer angegeben als die spezifische Wärmekapazität c.
Das hochgedämmte Konstruktionen oft zur Schimmelbildung neigen, muß sachgemäß bekämpft werden aber nicht indem man zu hohen Energieverlusten zurückkehrt. Schlecht gedämmte Fenster sind z.B. eine Feuchtigkeitsfalle. Früher war das Fenster die kälteste Stelle in der Wohnung. Stieg in der Wohnung die Luftfeuchtigkeit zu sehr an, so kondensierte am Fenster Tauwasser und begrenzte durch den Tauwasserausfall den Anstieg der Feuchtigkeit. Dadurch war für eine Schimmelbildung die Luftfeuchtigkeit zu gering. Heute ist z.B. manchmal die Außenwand hinter einem Schrank die kälteste Stelle, da zwar durch die hohe Wärmedämmung nur wenig Wärme verloren geht, aber durch den Schrank so wenig Wärme nachgeliefert wird, das die Wand doch der kälteste Punkt ist. Durch Tapetenleim usw. ist auch die Ernährungsbasis des Schimmels (im Gegensatz zur Fensterscheibe) gesichert.