Dipl.-Physiker Jochen Ebel
Die einschalige Wand mit Einschaltung oder periodischer Erregung
Inhaltsverzeichnis
1 Aufstellung der Gleichungen
2 Der periodische Fall bei Strahlung
2.1 konstante Innentemperatur
2.2 Ideale Innendämmung
3 Der periodische Fall bei Temperatur
3.1 konstante Innentemperatur
3.2 Ideale Innendämmung
4 Rechnung bei Strahlungseinschaltung
4.1 konstante Innentemperatur
4.2 ideale Dämmung
5 Rechnung bei Temperatureinschaltung
5.1 konstante Innentemperatur
5.2 ideale Dämmung
6 Anmerkungen zu Rechenprogrammen
6.1 Hyperbelfunktionen
6.2 Allgemeine Bemerkungen
6.3 Iteration bei konstanter Temperatur
6.4 Iteration bei idealer Dämmung
6.5 Programmbeispiel in VBA
6.5.1 ... für periodisch
6.5.2 ... für Einschaltung
7 Beispielkurven
7.1 Der periodische Fall
7.2 Der Einschaltfall
8 Literatur
1. Aufstellung der Gleichungen
Ausgangspunkt ist die bekannte Fouriersche Wärmeleitungsgleichung (siehe [1], [2] und [3]) in ihrer eindimensionalen Form:
(1) ![]()
![]() mit
mit![]() a =
a = ![]()
Betrachtet wird in dieser Abhandlung eine einschalige Wand der Breite w, auf die auf der Außenseite Strahlung einfällt oder der eine Temperatur aufgezwungen wird. Auf der Innenseite soll einmal die Temperatur konstant sein oder eine ideale Dämmung sein. Einiges von dem Nachfolgenden ist schon in [2] behandelt. Wegen der Geschlossenheit dieser Abhandlung kommt es zu Überschneidungen. Auch ist das Ziel von [2] die mehrschichtige Wand, deshalb kommen Matrizen zur Anwendung. Außerdem sind einige Druckfehler in [2].
Die Wahl der konstanten Temperatur zu 0 bedeutet keine Einschränkung der Allgemeinheit, da sich wegen der Linearität der Wärmeleitungsgleichung beliebige Lösungen überlagern lassen und damit an beliebige Werte angepaßt werden. Eine ideale Dämmung bedeutet, das an dieser Stelle kein Wärmestrom fließen kann.
Der einfallende Strahlungsverlauf E kann beliebig sein. Um Anhaltspunkte für beliebige Verläufe zu haben werden 2 Extremfälle ausgewählt:
Gesucht wird der Wärmestrom bzw. die Oberflächentemperatur der Wand. Dabei ist zu berücksichtigen, daß es bei steigender Wandtemperatur T zum Wärmeverlust in die Umgebung kommt. Damit entsteht folgende Gleichung (Dimension W/m2):
(2) E - ε T = -q
Bei der aufgezwungen Temperatur werden auch wieder 2 Fälle betrachtet:
Für alle Zeiten t < 0 ist Temperatur = 0°C und auch die Wand hat eine Temperatur von 0°C. Ab der Zeit t = 0 soll sich die Temperatur plötzlich auf einen Wert Te verändern.
Der Wand soll eine sinusförmige Temperatur aufgezwungen werden (siehe auch [5]). Auch bei der periodischen Temperatur wird der eingeschwungene Zustand betrachtet.
Durch die aufgezwungene Temperatur entsteht statt (2) die Identität:
(3) T = T
2. Der periodische Fall bei Strahlung
Zuerst wird der periodische Fall betrachtet. Für E wird eine Exponentialfkt angesetzt:
(4) E = E0 ![]()
Das ist wieder keine Einschränkung, wegen der Linearität der Wärmeleitungsgleichung ist auch die konjugiert komplexe Lösung von (4) wieder eine Lösung und die Addition einer Lösung und ihrer konjugiert komplexen Lösung liefert eine reelle Lösung.
Für T wird folgender Teilansatz gemacht:
(5) T = T0 ![]()
Gleichung (5) wird in (1) eingesetzt und T0 ![]() gekürzt. Damit entsteht eine Gleichung für κ:
gekürzt. Damit entsteht eine Gleichung für κ:
(6) i ω = a (1 + i)2 κ2 = 2 a i κ2 ![]() κ =
κ = 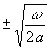
Endgültig wird für T folgender Ansatz gemacht:
(7) T = T0 [![]() ]
]
Mit dem oberen Vorzeichen wird oberen Vorzeichen wird gesichert, das bei x = w die Temperatur = 0 wird, da beide Terme in der eckigen Klammer gleich sind. Wegen der 2 möglichen Vorzeichen in (6) ist dieser Ansatz zulässig. Beim unteren Vorzeichen wird bei x = w der Wärmestrom zu 0 wie sich nachfolgend zeigt. Durch Differentation von (7) nach x und Multiplikation mit λ wird für den Wärmestrom:
(8) q = λ ![]() = - λ T0 (1 + i) κ [
= - λ T0 (1 + i) κ [![]() ]
]
In (2) wird (4), (7) und (8) bei x = 0 eingesetzt und ![]() gekürzt:
gekürzt:
(9) E0 - ε T0 [![]() ] = λ T0 (1 + i) κ [
] = λ T0 (1 + i) κ [![]() ]
]
Gleichung (9) ist nun nach T0 aufzulösen:
(10) T0 = ![]()
Um den Wärmestrom bei der konstanten Innenwandtemperatur an der Innenwand, d.h. bei x = w zu bestimmen, ist (10) in (8) einzusetzen und nur das obere Vorzeichen zu nehmen:
(11) q = ![]()
In (11) wird der Zähler gekürzt:
(12) q = 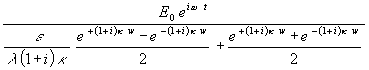
Der Bruch mit den e-Funktionen sind die Gleichungen der Hyperbelfunktionen:
(13) q = 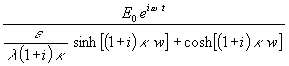
Mit
(14) q = qw ![]()
wird aus (13):
(15) qw = 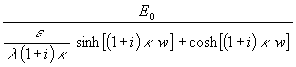
Zur weiteren Auswertung werden 2 Abkürzungen definiert:
(16) α = ![]()
![]() und
und![]() y = κ w
y = κ w
Obwohl die Speicherwirkung der Wand nicht im geringsten vernachlässigt wurde ist α das Verhältnis von Verlustkoeffizient ε zum U-Wert (= λ κ) einer hypothetischen Wand mit der Dicke 1/κ. Mit (16) wird aus (15):
(17) qw = 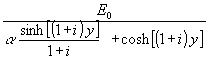
Für weitere Auswertungen wird Betrag und Phase im Nenner von (17) gebraucht. Das Quadrat des Betrages erhält man, wenn man den Nenner mit dem konjugiert komplexen Nenner (d.h. im Nennerausdruck i durch i ersetzen). Mit der Benutzung von Additionstheoremen der Hyperbelfunktionen
(18)
sinh(a + b) = sinha × coshb + cosha × sinhb
cosh(a + b) = cosha × coshb + sinha × sinhb
sinha × sinhb = ½ [cosh(a + b) cosh(a b)]
sinha × coshb = ½ [sinh(a + b) + sinh(a b)]
cosha × coshb = ½ [cosh(a + b) + cosh(a b)]
, den Beziehungen zwischen sin und cos
(19) cosh2 y sinh2 y = 1![]() cos2 y + sin2 y = 1
cos2 y + sin2 y = 1
und den Beziehungen zwischen Hyperbel- und trigonometrischen Funktionen
(20) sinh(iy) = i sin y![]() cosh(iy) = cos y
cosh(iy) = cos y![]() sin(iy) = i sinh y
sin(iy) = i sinh y![]() cos(iy) = cosh y
cos(iy) = cosh y
wird aus (17) nach weiteren elementaren Umformungen:
(21) qw = 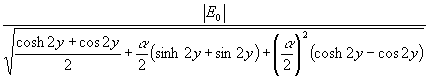
(Diagrammdarstellung Bild 2)
Interessant ist auch die asymptotische Näherung durch Potenzreihenentwicklung bis y2:
(22) qw ~ ![]()
![]() für
für![]() y −−> 0
y −−> 0
Die Wurzel im Nenner von (21) nimmt für y = 0 den Wert 1 an und steigt für steigendes y (steigende Wandstärke) monoton an, d.h. die Wärmestromamplitude (qw) auf der Innenseite der Wand ist immer kleiner als die einfallende Wärmestromamplitude (E0) und wird durch die Speicherwirkung der Wand bei steigender Wandstärke immer kleiner.
Hauptbestimmend für qw ist die e-Funktion (steckt in den Hyperbelfunktionen). Deswegen wird für (21) folgender Ansatz gemacht:
(23) qw = E0 e y H(y)
Aus (21) folgt mit (23):
(24) H(y) = 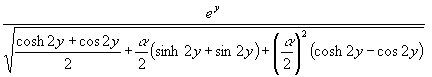
(Diagrammdarstellung Bild 1)
Der Grenzwert für große y kann auch angegeben werden:
(25) H(y) ~ 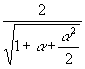
![]() für
für![]() y −−> ∞
y −−> ∞
Wie in Abschnitt 7.1 gezeigt wird, wird dieser Wert schon bei y > 3 sehr gut angenähert.
Für die Zeitverzögerung durch die Wand muß der Phasenwinkel bestimmt werden. Dazu ist im Nenner von (17) mit (18) und (20) der Real- und Imaginärteil des Nenners zu trennen. Das Verhältnis von Imaginär- und Realteil ist gleich dem tan des gesuchten Phasenwinkels φ:
(26) φq = atn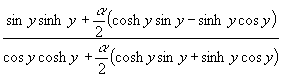 = atn
= atn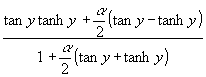
(Diagrammdarstellung Bild 5)
Mit der Potenzreihenentwicklung der Funktionen bis y2 ergibt sich folgende asymptotische Näherung:
(27) φq ~ y2![]() für
für![]() y −−> 0
y −−> 0
Für größere y der Ausdruck (26) mehrdeutig. Deswegen mache ich einen Ansatz
(28) φq = y + Δq und versuche den Ausdruck für Δ zu finden. Dazu brauche ich weitere Additionstheoreme:
(29) tan(y + Δ) = ![]()
![]() und
und![]() tan y =
tan y = ![]()
![]() und
und![]() cosh y sinh y = e-y
cosh y sinh y = e-y
Die letzte Gleichung folgt leicht aus der Definition der Hyperbelfunktionen. Aus (26) wird mit (28) und (29) und Umformungen (besonders mit cos2y = 1 sin2y bzw. sin2y = 1 cos2y):
(30) Δq = arctan 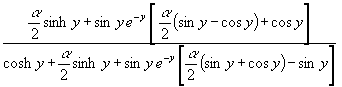 oder durch kürzen:
oder durch kürzen:
(Diagrammdarstellung Bild 4)
(31) Δq= atn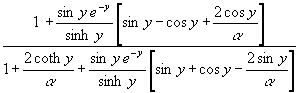 ==> Δq ~ atn
==> Δq ~ atn![]() für y −−> ∞
für y −−> ∞
Die rechte Seite von (31) ist für beliebige y kleiner als 1. Außerdem ist der Grenzwert für große y angegeben (coth wird dann 1). Für kleine y ist sie sogar gleich y, denn für kleine y muß in (28) das y kompensiert werden, damit die Näherung (27) erfüllt wird. Aber für beliebige y gilt wegen tan Δq < 1:
(32) Δq < 45°
Damit ist für konstante Innentemperatur die Lösung für die Heizleistung gefunden und einige Näherungen angegeben.
Es wird der Temperaturverlauf an der Innenseite der Wand, d.h. bei x = w bestimmt. Dazu wird (10) in (7) eingesetzt und die unteren Vorzeichen genommen:
(33) T = ![]()
Analoge Umformungen, die zu (17) geführt haben, ergeben aus (33):
(34) Tw = ![]()
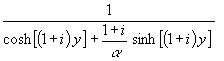
Dabei ist ![]() eine hypothetische Temperatur, die sich auf der Außenseite der Wand einstellen würde, wenn die Wand ideal wärmedämmend sein würde. Auch hier wird wieder analog Betrag und Phase im Nenner des zweiten Bruches bestimmt:
eine hypothetische Temperatur, die sich auf der Außenseite der Wand einstellen würde, wenn die Wand ideal wärmedämmend sein würde. Auch hier wird wieder analog Betrag und Phase im Nenner des zweiten Bruches bestimmt:
(35) Tw = ![]()
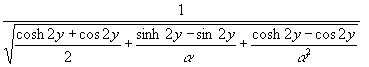
(Diagrammdarstellung Bild 2)
Interessant ist auch wieder die asymptotische Näherung durch Potenzreihenentwicklung bis y2 und mit der Näherung der Wurzel für kleine Abweichungen von 1:
(36) Tw ~ ![]()
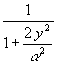
![]() für
für![]() y −−> 0
y −−> 0
Hauptbestimmend für qw ist wieder die e-Funktion (steckt in den Hyperbelfunktionen). Deswegen wird für (21) folgender Ansatz gemacht:
(37) Tw = E0 e y S(y)
Aus (35) folgt mit (37):
(38) S(y) = 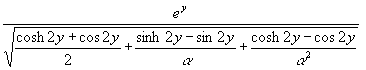
(Diagrammdarstellung Bild 1)
Der Grenzwert für große y kann auch angegeben werden:
(39) S(y) ~ ![]()
![]() für
für![]() y −−> ∞
y −−> ∞
Wie in Abschnitt 7.1 gezeigt wird, wird dieser Wert schon bei y > 3 sehr gut angenähert.
Für den Phasenwinkel ergibt sich:
(40) φt = arctan![]()
(Diagrammdarstellung Bild 5)
Mit der Potenzreihenentwicklung der Funktionen bis y ergibt sich folgende asymptotische Näherung:
(41) φt ~ ![]()
![]() für
für![]() y −−> 0
y −−> 0
Für größere y der Ausdruck (40) mehrdeutig. Deswegen mache ich einen Ansatz
(42) φt = y + Δt und versuche den Ausdruck für Δt analog zu (30) zu finden.
(43) Δt = arctan![]()
Durch Kürzen von sinh wird daraus:
(44) Δt = arctan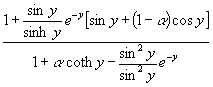 ==> Δt ~ atn
==> Δt ~ atn ![]()
![]() für
für![]() y −−> ∞
y −−> ∞
(Diagrammdarstellung Bild 4)
Die rechte Seite von (44) ist für beliebige y kleiner als 1. Außerdem ist der Grenzwert für große y angegeben (coth wird dann 1). Für kleine y ist wird wieder y kompensiert, damit die Näherung (41) erfüllt wird. Aber für beliebige y gilt wegen tan Δt < 1:
(45) Δt < 45°
Damit ist für ideale Innendämmung die Lösung für den Temperaturverlauf gefunden und einige Näherungen angegeben.
3. Der periodische Fall bei Temperatur
Zuerst wird der periodische Fall betrachtet. Für T wird eine Exponentialfkt angesetzt:
(46) Te = Te0 ![]()
Das ist wieder keine Einschränkung, wegen der Linearität der Wärmeleitungsgleichung ist auch die konjugiert komplexe Lösung von (46) wieder eine Lösung und die Addition einer Lösung und ihrer konjugiert komplexen Lösung liefert eine reelle Lösung.
Für T wird ein zu (5) entsprechender Teilansatz gemacht, der dann wieder zu κ führt:
(47) T = Tp ![]()
Endgültig wird für T folgender Ansatz gemacht:
(48) T = Tp [![]() ]
]
Mit dem oberen Vorzeichen wird oberen Vorzeichen wird gesichert, das bei x = w die Temperatur = 0 wird, da beide Terme in der eckigen Klammer gleich sind. Wegen der 2 möglichen Vorzeichen in (6) ist dieser Ansatz zulässig. Beim unteren Vorzeichen wird bei x = w wieder der Wärmestrom zu 0. Allgemein gilt für den Wärmestrom entsprechend:
(49) q = λ ![]() = - λ Tp (1 + i) κ [
= - λ Tp (1 + i) κ [![]() ]
]
In (3) wird (48) bei x = 0 eingesetzt und ![]() gekürzt:
gekürzt:
(50) Te0 = Tp [![]() ]
]
Gleichung (50) ist nun nach Tp aufzulösen:
(51) Tp = ![]()
Um den Wärmestrom bei der konstanten Innenwandtemperatur an der Innenwand, d.h. bei x = w zu bestimmen, ist (51) in (48) einzusetzen und nur das obere Vorzeichen zu nehmen:
(52) q = 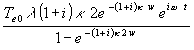
In (52) wird der Zähler gekürzt:
(53) q = 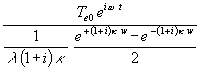
Der Bruch mit den e-Funktionen sind die Gleichung einer Hyperbelfunktion:
(54) q = 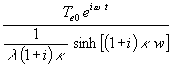
Mit
(55) q = qp ![]()
wird aus (54):
(56) qp = 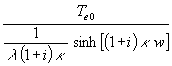
Mit den Abkürzungen (16) wird aus (56):
(57) qp = 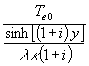 =
= 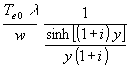
Für weitere Auswertungen wird wieder Betrag und Phase im Nenner von (57) gebraucht. Nach Umformungen entsprechend (21) wird:
(58) qp = 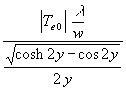 =
= 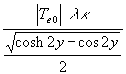
(Diagrammdarstellung Bild 2)
Interessant ist auch die asymptotische Näherung durch Potenzreihenentwicklung bis y2:
(59) qw ~
![]()
![]() für
für![]() y −−> 0
y −−> 0
Der Nenner von (58) nimmt für y −−> 0 den Wert 1 an und steigt für steigendes y (steigende Wandstärke) monoton an, d.h. die Wärmestromamplitude (qw) auf der Innenseite der Wand ist immer kleiner als der stationäre Wärmestrom (![]() ) und wird durch die Speicherwirkung der Wand bei steigender Wandstärke immer kleiner.
) und wird durch die Speicherwirkung der Wand bei steigender Wandstärke immer kleiner.
Hauptbestimmend für qp ist die e-Funktion (steckt in den Hyperbelfunktionen). Deswegen wird für (58) folgender Ansatz gemacht:
(60) qw = ![]() e y H(y)
e y H(y)
Aus (58) folgt mit (60):
(61) H(y) = 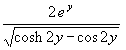
(Diagrammdarstellung Bild 1)
Der Grenzwert für große y kann auch angegeben werden:
(62) H(y) ~ ![]()
![]() für
für![]() y −−> ∞
y −−> ∞
Wie in Abschnitt 7.1 gezeigt wird, wird dieser Wert schon bei y > 3 sehr gut angenähert.
Für die Zeitverzögerung durch die Wand muß der Phasenwinkel bestimmt werden. Dazu ist im Nenner von (57) der Real- und Imaginärteil des Nenners zu trennen. Das Verhältnis von Imaginär- und Realteil ist gleich dem tan des gesuchten Phasenwinkels φ:
(63) φq = arctan ![]() = arctan
= arctan ![]()
(Diagrammdarstellung Bild 5)
Mit der Potenzreihenentwicklung der Funktionen bis y3 ergibt sich folgende asymptotische Näherung:
(64) φq ~ ![]()
![]() für
für![]() y −−> 0
y −−> 0
Für größere y der Ausdruck (26) mehrdeutig. Deswegen mache ich einen Ansatz
(65) φq = y + Δq
und versuche den Ausdruck für Δ zu finden. Aus (63) wird mit (65) und Umformungen:
(66) Δq = arctan ![]() ==> Δq ~ - atn(1)
==> Δq ~ - atn(1)![]() für
für![]() y −−> ∞
y −−> ∞
(Diagrammdarstellung Bild 4)
Für beliebige y überschreitet (66) 1 nur unwesentlich. Außerdem ist der Grenzwert für große y angegeben. Für kleine y ist Δq sogar gleich y, denn für kleine y muß in (65) das y kompensiert werden, damit die Näherung (64) erfüllt wird.
Damit ist für konstante Innentemperatur die Lösung für die Heizleistung gefunden und einige Näherungen angegeben.
Es wird der Temperaturverlauf an der Innenseite der Wand, d.h. bei x = w bestimmt. Dazu wird (51) in (48) eingesetzt und die unteren Vorzeichen genommen:
(67) T = ![]()
Analoge Umformungen, die zu (17) geführt haben, ergeben aus (67):
(68) Tw = ![]()
Auch hier wird wieder analog Betrag und Phase im Nenner des Bruches bestimmt:
(69) Tw = 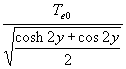
(Diagrammdarstellung Bild 2)
Interessant ist auch wieder die asymptotische Näherung durch Potenzreihenentwicklung bis y4 und mit der Näherung der Wurzel für kleine Abweichungen von 1:
(70) Tw ~ ![]()
![]() für
für![]() y −−> 0
y −−> 0
Hauptbestimmend für qw ist wieder die e-Funktion (steckt in den Hyperbelfunktionen). Deswegen wird für (21) folgender Ansatz gemacht:
(71) Tw = Te0 e y S(y)
Aus (69) folgt mit (71):
(72) S(y) = 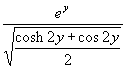
(Diagrammdarstellung Bild 1)
Der Grenzwert für große y kann auch angegeben werden:
(73) S(y) ~ 2![]() für
für![]() y −−> ∞
y −−> ∞
Wie in Abschnitt 7.1 gezeigt wird, wird dieser Wert schon bei y > 3 sehr gut angenähert.
Für den Phasenwinkel ergibt sich:
(74) φt = arctan(tanh y tan y)
(Diagrammdarstellung Bild 5)
Mit der Potenzreihenentwicklung der Funktionen bis y ergibt sich folgende asymptotische Näherung:
(75) φt ~ y2![]() für
für![]() y −−> 0
y −−> 0
Für größere y der Ausdruck (40) mehrdeutig. Deswegen mache ich wieder den Ansatz:
(76) φt = y + Δt und versuche den Ausdruck für Δt analog zu (30) zu finden.
(77) Δt = arctan![]() = arctan
= arctan![]() ==> Δ t ~ 0
==> Δ t ~ 0![]() für
für![]() y −−> ∞
y −−> ∞
(Diagrammdarstellung Bild 4)
Δt in (77) ist für beliebige y kleiner als 1. Für kleine y wird wieder y kompensiert, damit die Näherung (75) erfüllt wird.
Damit ist für ideale Innendämmung die Lösung für den Temperaturverlauf gefunden und einige Näherungen angegeben.
4. Rechnung bei Strahlungseinschaltung
Vorstehende Aufgabe wird zweckmäßig mit der Laplacetransformation behandelt, siehe [4]. Dort wurde die Wärmeausbreitung in einem ∞ ausgedehnten Medium durch das Faltungsintegral mit einer Gewichtsfunktion G beschrieben, wenn an einem Ort der Temperaturverlauf T vorgegeben wird. Bei der Laplacetransformation geht die Faltung in ein Produkt aus dem laplacetransformierten Temperaturverlauf TL und der laplacetransformierten Gewichtsfunktion über. Für die Laplacetransformierte der Gewichtsfunktion wurde gefunden:
(78) ![]()
![]() mit
mit![]()
![]()
Analog (7) wird für die laplacetransformierte Temperatur TL folgender Ansatz gemacht:
(79) TL = TeL (![]() )
)
Eine andere Vorstellung, die zu (79) führt, benutzt die Linearität der Wärmeleitungsgleichung. Dazu stellt man sich ein beidseitig ∞ mit dem Wandmaterial ausgefüllten Raum vor, indem die Lösung für einen vorgegebenen Temperaturverlauf bei x = 0 und der Lösung für einen gleichen (oberes Vorzeichen) oder entgegengesetzten (unteres Vorzeichen) Temperaturverlauf bei x = 2w addiert werden. Schneidet man das Medium bei x = 0 und x = w ab, so ändert sich in dem stehengebliebenen Teil (Wand) nichts und man erhält (79).
Differenziert man (79) nach x (zulässig, da die Differentation nach x im Sinne der Laplacetransformation die Differentation nach einem Parameter ist) und multipliziert mit dem Wärmeleitkoeffizienten λ, so erhält man die Laplacetransformierte des Wärmestroms:
(80) qL = λ![]() = - λ TeL
= - λ TeL ![]() (
(![]() )
)
Laplacetransformiert man jetzt (2) (die Laplacetransformierte der Einschaltfunktion E ist = E0/p) und setzt (79) und (80) ein, so erhält man an der Stelle x = 0:
(81) ![]() - ε TeL (
- ε TeL (![]() ) = λTeL
) = λTeL ![]() (
(![]() )
)
(81) hat die Form einer algebraischen Gleichung und wird nach TeL aufgelöst:
(82) TeL = 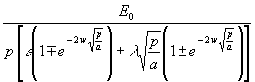
Verschiedene Konstanten lassen sich zum Wärmeeindringkoeffizienten b zusammenfassen [1]. Dabei hat b in SI-Einheiten die Dimension Ws½/m2K:
(83) b = ![]()
Mit (83) wird aus (82), wenn noch ε aus der eckigen Klammer herausgezogen wird:
(84) TeL = ![]()
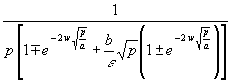
Theoretisch könnte man (84) rücktransformieren. Die Rücktransformation von (84) ist für w −−> ∞ (Wegfall der e-Funktionen) in [4] auf der Basis der Tabellen [8] geschehen. Das war schwierig, weil ![]() stets 2 Lösungen hat, die sich im Vorzeichen unterscheiden. Dadurch ist die Funktion nur auf einer zweiblättrigen Fläche (genauer in der Funktionentheorie erklärt) eindeutig. Das macht die Rücktransformation so schwierig. Für die Rücktransformation für w = endlich helfen die Tabellen [8] wenig. Aber der Zeitverlauf von Te interessiert auch wenig.
stets 2 Lösungen hat, die sich im Vorzeichen unterscheiden. Dadurch ist die Funktion nur auf einer zweiblättrigen Fläche (genauer in der Funktionentheorie erklärt) eindeutig. Das macht die Rücktransformation so schwierig. Für die Rücktransformation für w = endlich helfen die Tabellen [8] wenig. Aber der Zeitverlauf von Te interessiert auch wenig.
Im weiteren müssen die 2 Fälle wieder getrennt behandelt werden.
Dazu ist (84) in (80) einzusetzen und es wird die Heizleistung an der Stelle x = w gesucht (es sind also die oberen Vorzeichen zu nehmen) und anschließend wird gekürzt:
(85) qwL = ![]()
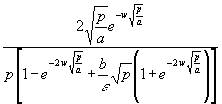 = qwL =
= qwL = ![]()
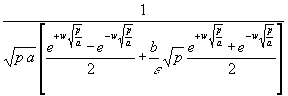
Die Brüche in (85) sind wieder Hyperbelfunktionen. Damit und dem Hineinziehen von ε/λ in die Klammer wird bei Berücksichtigung von (83):
(86) qwL = ![]()
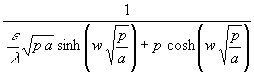
Aussagefähig sind wieder asymptotische Grenzwerte für t −−> 0 bzw. ∞ der Rücktransformierten:
(87) qw(0) = ![]() = 0
= 0
Zweckmäßig wird für das weitere eine Konstante β definiert:
(88) β = ![]()
Diese Konstante definiert das Verhältnis von Verlust (durch ε) und den stationären Wärmestrom durch den U-Wert (λ/w). Damit wird:
(89) qw(∞) = ![]() =
= ![]()
Diese Grenzwerte waren auch zu erwarten. Auf der anderen Seite der Wand kann beim Einschalten der Strahlungsquelle (t = 0) noch keine Heizleistung gebraucht werden und im stationären Endzustand (t −−> ∞) teilt sich die einfallende Strahlung in den Verlust und den stationären Wärmestrom.
Noch besser ist natürlich die Rücktransformation von (86). Im Gegensatz zu (84) ist (86) einfacher rückzutransformieren. Zwar hat ![]() immer noch 2 Lösungen, die sich im Vorzeichen unterscheiden. Sieht man sich die Funktion aber genauer an, sieht man, das beide Lösungen zu dem gleichen Funktionswert führen. Der cosh hat bei Vorzeichenwechsel des Arguments den gleichen Wert wie ohne Vorzeichenwechsel. Der sinh wechselt bei Vorzeichenwechsel des Arguments zwar auch das Vorzeichen, aber da mit dem Argument multipliziert wird, wechselt das Vorzeichen zweimal. Dadurch ist der Wert des Produkts unabhängig vom Vorzeichenwechsel. Eine zweite Erklärung geht von der Entwicklung der Funktionen aus. Beim cosh treten nur geradzahlige Potenzen des Arguments auf. Dadurch verschwindet die Wurzel. Beim sinh treten nur ungerade Potenzen des Arguments auf. Da aber mit
immer noch 2 Lösungen, die sich im Vorzeichen unterscheiden. Sieht man sich die Funktion aber genauer an, sieht man, das beide Lösungen zu dem gleichen Funktionswert führen. Der cosh hat bei Vorzeichenwechsel des Arguments den gleichen Wert wie ohne Vorzeichenwechsel. Der sinh wechselt bei Vorzeichenwechsel des Arguments zwar auch das Vorzeichen, aber da mit dem Argument multipliziert wird, wechselt das Vorzeichen zweimal. Dadurch ist der Wert des Produkts unabhängig vom Vorzeichenwechsel. Eine zweite Erklärung geht von der Entwicklung der Funktionen aus. Beim cosh treten nur geradzahlige Potenzen des Arguments auf. Dadurch verschwindet die Wurzel. Beim sinh treten nur ungerade Potenzen des Arguments auf. Da aber mit ![]() multipliziert wird werden aus den ungeraden Potenzen gerade Potenzen und wieder verschwindet die Wurzel. Dadurch ist die Funktion auf einer einblättrigen Fläche (genauer in der Funktionentheorie erklärt) eindeutig. Das macht die Rücktransformation einfacher. Zuerst die Formel für die Rücktransformation, wenn dieses Integral existiert:
multipliziert wird werden aus den ungeraden Potenzen gerade Potenzen und wieder verschwindet die Wurzel. Dadurch ist die Funktion auf einer einblättrigen Fläche (genauer in der Funktionentheorie erklärt) eindeutig. Das macht die Rücktransformation einfacher. Zuerst die Formel für die Rücktransformation, wenn dieses Integral existiert:
(90) f(t) = 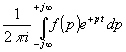
Wenn das nachfolgende Integral auch existiert, d.h. der Wert auf im ∞ der linken Halbebene gleich 0 ist (wie im vorliegenden Fall, können die Integrationsgrenzen im ∞ geschlossen werden, so daß die Lösung mit Residuen möglich ist:
(91) f(t) = ![]() =
= ![]()
Nun sind die Residuen zu bestimmen. Das sind hier speziell die Polstellen von f(p) bzw. die Nullstellen des Nenners. Nach [7, S. 66ff] ist an diesen Stellen ist der Nenner um die Nullstelle zu entwickeln und der Wert mit ept (Zählerwert) und 2πi an dieser Stelle zu multiplizieren. Bei einfachen Nullstellen (wie hier) ist die Entwicklung die erste Ableitung wegen f(z) = f(z0) + f ´ (z0) (z - z0) + ....
Nun sind die Nullstellen des Nenners in (86) zu bestimmen. D.h.:
(92) N(p) = 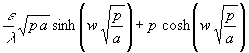 = 0
= 0
In (92) wird der Faktor vor dem sinh gekürzt:
(93) 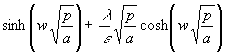 = 0
= 0
Der Einfachheit halber wird eine Variable z definiert und eine Konstante β (88) benutzt:
(94) z = ![]()
β ist das Verhältnis von U-Wert (λ/w) zu Verlust (durch ε). Mit (94) wird aus (93):
(95) ![]() = 0
= 0
Eine Lösung von (95) ist z0 = 0. Setzt man für z einen beliebigen komplexen Wert z = x + iy an und trennt dann in (95) Realteil und Imaginärteil, so müssen für eine Nullstelle beide gleichzeitig Null sein. Das Ergebnis zeigt, daß das nur möglich ist, wenn mindestens x = 0 ist. Daher existieren für reelle z keine weiteren Lösungen. Für den Imaginärteil mit
(96) z = iy
geht nach Kürzen von i/β (95) über in:
(97) ![]() = 0
= 0
Diese Gleichung hat ∞ viele Lösungen (siehe Abschnitt 6). Mit (94) und (96) folgt daraus für p0:
(98) p0 = ![]()
Gleichung (98) legt es nahe für die Wand eine Zeitkonstante zu definieren (z.B. in [9, S. 116] als Auskühlzeit bezeichnet):
(99) tw = ![]()
Mit (99) wird aus(98):
(100) p0 = ![]()
Nun ist der Wert der Residuen zu bestimmen. Dazu ist als erstes die Ableitung des Nenners von (86) zu bestimmen:
(101) N´(p) = 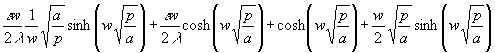
Da der Wert von (101) nur an den Nullstellen von N(p) interessiert, wird mit (94) und (96):
(102) N´(p0) = ![]()
Mit der ersten Gleichung von (97) läßt sich (102) noch einfacher darstellen:
(103) N´(p0) = -![]()
Aus (91) wird mit (100) und (103) für den gesuchten Heizleistungsverlauf:
(104) qw(t) = E0 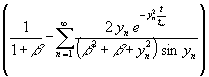
Oder bei Normierung auf den Endwert:
(105) qw(t) = ![]()
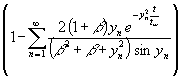
Für den Spezialfall β = 0 (damit wird nach (97) yn = (n ½) π) läßt sich (104) noch weiter vereinfachen:
(106) qw(t) = E0 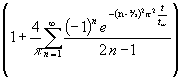
(Diagrammdarstellung Bild 7)
Gleichung (106) ermöglicht noch eine Kontrolle: Aus der asymptotischen Betrachtung (87) ergibt sich, daß (106) für t = 0 ebenfalls 0 sein muß. Für t = 0 werden die e-Funktionen in der Summe zu 1 und brauchen deshalb nicht berücksichtigt zu werden. Damit qw(0) zu 0 wird, muß der verbleibende Summenausdruck = - π/4 sein. [6, S. 82, Formel 6.] zeigt, daß das der Fall ist.
Zur Normierung hat sich hier die Auskühlzeit tw (99) angeboten, da sie nur von Materialeigenschaften und Wand abhängt. Bezieht man noch die Oberflächeneigenschaften (ausgedrückt durch den Verlustkoeffizient ε) ein, lassen sich die Dicke w0 einer Bezugswand und eine Zeit tN definieren:
(107) w0 = ![]()
![]() tN =
tN = ![]()
Mit der Beziehung für β {Gleichung (88) β = ![]() } wird:
} wird:
(108) w = β w0![]() tw = β2 tN =
tw = β2 tN = ![]() {Gleichung (99)}
{Gleichung (99)}
Dazu ist (84) in (79) einzusetzen und es wird der Temperaturverlauf an der Stelle x = w gesucht (es sind also die unteren Vorzeichen zu nehmen) und anschließend wird gekürzt:
(109) TwL = ![]()
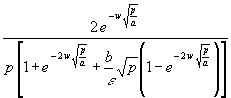
TwL = ![]()
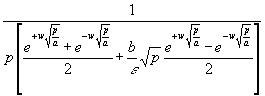
Die Brüche in (109) sind wieder Hyperbelfunktionen. Damit wird bei Berücksichtigung von (83):
(110) TwL = ![]()
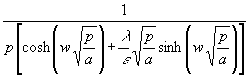
Mit (88) wird aus (110):
(111) TwL = ![]()
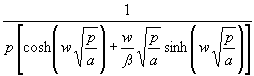
Aussagefähig sind wieder asymptotische Grenzwerte für t −−> 0 bzw. ∞ der Rücktransformierten:
(112) Tw(0) = ![]() = 0
= 0
(113) Tw(∞) = ![]() =
= ![]()
Diese Grenzwerte waren auch zu erwarten. Auf der anderen Seite der Wand kann beim Einschalten der Strahlungsquelle (t = 0) noch kein Temperaturanstieg sein und im stationären Endzustand (t −−> ∞) kann die einfallende Strahlung nur über den Verlust abgestrahlt werden.
Zur Rücktransformation von (111) ist wieder festzustellen, daß trotz der Wurzeln die Funktion auf einer einblättrigen Fläche eindeutig ist. Damit sind wieder die Nullstellen des Nenners zu ermitteln. Eine Nullstelle ist wieder p = 0. Mit (94) geht die eckige Klammer über in:
(114) cosh z + ![]() sinh z = 0
sinh z = 0
Für reelles z ist auch (114) nicht zu erfüllen. Mit (96) geht (114) über in:
(115) cos y ![]() sin y = 0
sin y = 0
Vorstehende Gleichung hat wieder ∞ viele Lösungen (siehe Abschnitt 6).
Zum weiteren Lösungsweg wird wieder die Ableitung der eckigen Klammer in (111) gebraucht:
(116) [ ]´ = 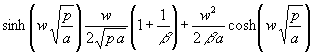
Multipliziert man (116) noch mit p erhält man für den Nenner:
(117) N´(p) =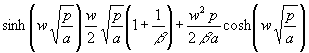
Mit (94) und (96) erhält man daraus (verbessert mit (115)):
(118) N´(p0) = 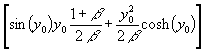 =
= ![]()
Mit (118) ergibt sich die gesuchte Lösung analog (104):
(119) Tw(t) = ![]()
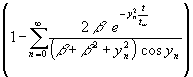
(Diagrammdarstellung Bild 9)
Eine Kontrollmöglichkeit besteht auch hier für β −−> 0. In Abschnitt 6.4 ist gezeigt, daß dann der Wert y0 −−> ![]() geht, während die anderen yn alle > π sind. Damit reduziert sich die Summe auf ihr 0tes Glied, denn der Zähler ist sehr klein und nur bei y0 ist auch der Nenner klein von 2 β, wegen
geht, während die anderen yn alle > π sind. Damit reduziert sich die Summe auf ihr 0tes Glied, denn der Zähler ist sehr klein und nur bei y0 ist auch der Nenner klein von 2 β, wegen ![]() ≈ β. Dagegen ist β
2 zu vernachlässigen. Damit wird aus (119) (der cos wird für kleine ß zu 1):
≈ β. Dagegen ist β
2 zu vernachlässigen. Damit wird aus (119) (der cos wird für kleine ß zu 1):
(120) Tw(t) = ![]()
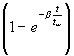
![]() für
für![]() β −−> 0
β −−> 0
Für t = 0 wird dann Tw(0) = 0. Für kleine β-Werte ist noch zu berücksichtigen, das in β auch ε steckt (88). Für kleine Zeiten reicht die Entwicklung der e-Funktion bis zum 1. Glied. ε läßt sich dann kürzen und man erhält, wenn man auch noch (99) und (1) berücksichtigt:
(121) Tw(t) = ![]()
![]() für
für![]() β −−> 0 und t << tw/ß und damit genau das Ergebnis des Lichtenfelder Experiments [10]. Also die Speicherwirkung ist ein wesentlicher Wert für den Anstieg der Temperatur. Und da der bei Dämmstoffen gering ist, folgt ein schneller Anstieg der Temperatur. Dagegen ist die Wärmeleitfähigkeit des Stoffes ohne Einfluß.
β −−> 0 und t << tw/ß und damit genau das Ergebnis des Lichtenfelder Experiments [10]. Also die Speicherwirkung ist ein wesentlicher Wert für den Anstieg der Temperatur. Und da der bei Dämmstoffen gering ist, folgt ein schneller Anstieg der Temperatur. Dagegen ist die Wärmeleitfähigkeit des Stoffes ohne Einfluß.
5. Rechnung bei Temperatureinschaltung
Vorstehende Aufgabe wird auch wieder mit der Laplacetransformation behandelt. Für Temperatur und Heizung wurden in Abschnitt 4 die Gleichungen (79) und (80) gefunden.
Laplacetransformiert man jetzt (3) (die Laplacetransformierte der Einschaltfunktion T ist = T0/p) und setzt (79) und (80) ein, so erhält man an der Stelle x = 0:
(122) ![]() = TeL (
= TeL (![]() )
)
(122) hat die Form einer algebraischen Gleichung und wird nach TeL aufgelöst:
(123) TeL = 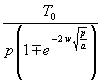
Im weiteren müssen die 2 Fälle wieder getrennt behandelt werden.
Dazu ist (123) in (80) einzusetzen und es wird die Heizleistung an der Stelle x = w gesucht (es sind also die oberen Vorzeichen zu nehmen) und anschließend wird gekürzt:
(124) qwL = T0 λ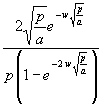 = T0 λ
= T0 λ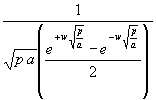
Der Bruch in (124) ist wieder eine Hyperbelfunktion. Damit wird:
(125) qwL = 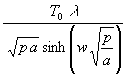
Aussagefähig sind wieder asymptotische Grenzwerte für t −−> 0 bzw. ∞ der Rücktransformierten:
(126) qw(0) = ![]() = 0
= 0
Mit dem U-Wert:
(127) U = ![]()
wird:
(128) qw(∞) = ![]() = T0 U
= T0 U
Diese Grenzwerte waren auch zu erwarten. Auf der anderen Seite der Wand kann beim Einschalten der Temperatur (t = 0) noch keine Heizleistung gebraucht werden und im stationären Endzustand (t −−> ∞) muß sich der stationäre Wärmestrom einstellen.
Nun ist (125) rückzutransformieren. Dazu sind wieder die Residuen zu bestimmen. Das sind hier speziell die Polstellen von f(p) bzw. die Nullstellen des Nenners. Nach [7, S. 66ff] ist an diesen Stellen ist der Nenner um die Nullstelle zu entwickeln und der Wert mit ept (Zählerwert) und 2πi an dieser Stelle zu multiplizieren. Bei einfachen Nullstellen (wie hier) ist die Entwicklung die erste Ableitung wegen f(z) = f(z0) + f ´ (z0) (z - z0) + ....
Nun sind die Nullstellen des Nenners in (125) zu bestimmen. D.h.:
(129) N(p) = 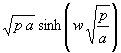 = 0
= 0
Der Einfachheit halber wird eine Variable z definiert:
(130) z = ![]()
Damit wird:
(131) ![]() = 0
= 0
Eine Lösung von (131) ist z0 = 0. Setzt man für z einen beliebigen komplexen Wert z = x + iy an und trennt dann in (131) Realteil und Imaginärteil, so müssen für eine Nullstelle beide gleichzeitig Null sein. Das Ergebnis zeigt, daß das nur möglich ist, wenn mindestens x = 0 ist. Daher existieren für reelle z keine weiteren Lösungen. Für den Imaginärteil mit
(132) z = iy
geht (131) über in:
(133) ![]() = 0
= 0
Diese Gleichung hat ∞ viele Lösungen:
(134) y0 = n π![]() mit
mit![]() n = 0, 1, 2, ... ∞
n = 0, 1, 2, ... ∞
Mit (130) und (134) folgt daraus für p0:
(135) p0 = ![]()
Mit der Konstante (99) wird:
(136) p0 = ![]()
Nun ist der Wert der Residuen zu bestimmen. Dazu ist als erstes die Ableitung des Nenners von (125) zu bestimmen:
(137) N´(p) = 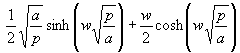
Da der Wert von (137) nur an den Nullstellen von N(p) interessiert, wird mit (132) und (134) (bei p = 0 ist der lim des 1. Terms zu berücksichtigen):
(138) N´(0) = w N´(p0) = ![]()
![]() mit
mit![]() n = 1, 2, ... ∞
n = 1, 2, ... ∞
Der cos läßt sich noch einfacher darstellen:
(139) N´(0) = w N´(p0) = ![]() (1)n
(1)n![]() mit
mit![]() n = 1, 2, ... ∞
n = 1, 2, ... ∞
Aus (125) wird mit (127) und (139) für den gesuchten Heizleistungsverlauf:
(140) qw(t) = U T0 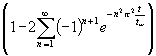
(Diagrammdarstellung Bild 7)
Bei Gleichung (140) muß der Sonderfall t = 0 extra betrachtet werden: Aus der asymptotischen Betrachtung (126) ergibt sich, daß (140) für t = 0 ebenfalls 0 sein muß. Für t = 0 werden die e-Funktionen in der Summe zu 1 und deshalb ensteht eine alternierende Folge, wenn ausgehend von n = 1 jeweils ein Glied der Reihe hinzunimmt. Damit strebt auf diesem Wege die Reihe keinem Endwert zu, nur der Mittelwert ist 0. Es müßte deshalb eine Grenzwertbetrachtung für t −−> 0 angestellt werden.
Dazu ist (84) in (79) einzusetzen und es wird der Temperaturverlauf an der Stelle x = w gesucht (es sind also die unteren Vorzeichen zu nehmen) und anschließend wird gekürzt:
(141) TwL = T0 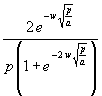 =
= 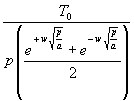 =
= 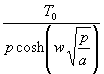
Aussagefähig sind wieder asymptotische Grenzwerte für t −−> 0 bzw. ∞ der Rücktransformierten:
(142) Tw(0) = ![]() = 0
= 0
(143) Tw(∞) = ![]() = T0
= T0
Diese Grenzwerte waren auch zu erwarten. Auf der anderen Seite der Wand kann beim Einschalten der Temperatur (t = 0) noch kein Temperaturanstieg sein und im stationären Endzustand (t −−> ∞) muß überall die angelegte Temperatur herrschen.
Zur Rücktransformation von (141) sind wieder die Polstellen zu ermitteln. Damit sind wieder die Nullstellen des Nenners zu ermitteln. Eine Nullstelle ist wieder p = 0. Die anderen ergeben sich aus:
(144) cosh z = 0
Für reelles z ist auch (114) nicht zu erfüllen. Mit (96) geht (144) über in:
(145) cos y0 = 0
Vorstehende Gleichung hat wieder ∞ viele Lösungen:
(146) y0 = (n ½ ) π![]() mit
mit![]() n = 1, 2, ... ∞
n = 1, 2, ... ∞
Zum weiteren Lösungsweg wird wieder die Ableitung des cosh des Nenners (141) gebraucht:
Multipliziert man (116) noch mit p erhält man für den Nenner:
(147) p cosh´(...) =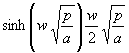
Mit (94) und (96) erhält man daraus (verbessert mit (115)):
(148) N(0) = 1 N(p0) = (-1)n (n ½ ) π/2 mit n = 1, 2, ... ∞
Mit (118) ergibt sich die gesuchte Lösung analog (104):
(149) Tw(t) = T0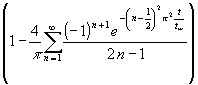
![]() mit
mit![]() tw =
tw = ![]() {Gleichung (99)}
{Gleichung (99)}
(Diagrammdarstellung Bild 9)
Der Klammerausdruck ist derselbe wie in (106), auch mit der Kontrollmöglichkeit.
6. Anmerkungen zu Rechenprogrammen
Bei vielen Rechenprogrammen sind die Hyperbelfunktionen nicht integriert. Deswegen muß auf die Definition der Hyperbelfunktionen mit e-Funktionen zurückgreifen. Die sind in fast allen Programmen integriert.
Die wirklichen Zeiten ergeben sich aus der normierten Zeit:
(150) t = x tw
Bei den unendlichen Summen kann man natürlich nicht alle Glieder berücksichtigen und muß die Reihe irgendwann abbrechen. Da die Reihen alternierend1) sind, ist der Fehler zur Summe immer kleiner als das erste weggelassene Glied. Allerdings ist die Konvergenz der Summe gering, so daß viele Glieder genommen werden müssen. Besonders bei kleinen Zeiten trifft das zu, wo die e-Funktionen noch groß sind. Deshalb wird nach der Kontrolle, das der Algorithmus bei t = 0 auch annähernd den Wert 0 liefert, dieser Wert auf 0 gesetzt.
Bei größeren Werten von x konvergieren die Reihen schneller. Deswegen kann nach einer Abschätzung des Restfehlers die Reihe abgebrochen werden.
Zur Tabellenberechnung kann eine Funktionsprozedur aufgerufen werden. Damit die Koeffizienten nicht bei jedem Funktionsaufruf neu berechnet werden müssen (Zeitaufwand), empfiehlt es sich, die Koeffizienten nicht lokal, sondern global abzuspeichern. Wegen des großen Feldes können nicht viele Felder angelegt werden, sondern man sollte sich mit einem begnügen. Das verlangt aber, das bei jedem Funktionsaufruf überprüft werden muß, ob das globale Feld auch für den vorliegenden Funktionsaufruf zutrifft oder neu berechnet werden muß.
6.3 Iteration bei konstanter Temperatur
Zur Berechnung der nicht geschlossen darstellbaren Werte werden Iterationsverfahren benutzt. (97) kann in nachfolgende 2 Gleichungen umgeformt werden:
(151) β![]() oder
oder ![]()
Hält man sich die graphische Darstellung des tan vor Auge, der in Schritten von π periodisch von -∞ nach +∞ geht, wird klar, daß es ∞ viele Schnittpunkte mit einer Geraden gibt, d.h. die vorstehende Gleichung hat ∞ viele Lösungen. Aus der Anschauung ergibt sich, das im Bereich von (n ½ )π bis nπ jeweils eine Lösung liegt.
Ausgehend von einem Startpunkt kann durch Iteration die Lösung beliebig genau gefunden werden. Voraussetzung ist aber, daß die Iteration konvergiert. Dazu wird (151) für die Iteration aufbereitet. Berücksichtigt muß auch werden, daß die Rechenprogramme im allgemeinen nur den Hauptwert des arctan liefern.
(152) ![]()
Voraussetzung zur Anwendung einer Iteration ist, daß die Iteration konvergiert. Bei (152) verlangt das, das der Betrag der ersten Ableitung der Funktion < 1 ist:
(153) 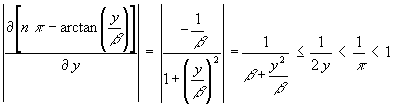
Die erste Ungleichung entsteht dadurch, daß das β gesucht wird, das bei gegebenen y den Nenner minimal (d.h. den Bruch maximal) macht. Die zweite Ungleichung entsteht dadurch, daß das kleinstmögliche y (d.h. < π/2) betrachtet wird und die 3. Ungleichung muß für Konvergenz erfüllt sein und ist auch. Hätte man in (151) statt der rechten die linke Gleichung genommen, wäre die Konvergenzbedingung nur in Spezialfällen zu erfüllen gewesen.
Zum Abbruch der Iteration gibt es 2 Methoden. 1. Abbruch, wenn ym + 1 ≈ ym ist. Je nach geforderter Genauigkeit ist das früher oder später der Fall. 2. nach einer bestimmten Anzahl der Iterationschritte wenn der Konvergenzfaktor bei jedem Schritt bekannt ist. Bei einem Anfangsfehler π/2 und dem Konvergenzfaktor 1/π reichen für einen Restfehler von 10-8 17 Schritte. Gewählt werden zur Sicherheit 20.
Jede Iteration braucht einen Startwert. Durch günstige Wahl des Startwertes konvergiert die Iteration schnell. Zweckmäßig erscheint hier:
(154) yStart = n π arctan(![]() )
)![]() mit
mit![]() n = 1, 2, 3, .. ∞
n = 1, 2, 3, .. ∞
Zur Abschätzung bis zu welchen Glied die Reihe berechnet werden muß, wird von (105) ausgegangen. Das nte Glied soll < 10-k sein. Damit entsteht:
(155) 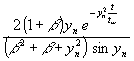 < 10-k
< 10-k
Zur Abschätzung wird bei yn von den Startwerten (154) ausgegangen. Der wird nach unten abgeschätzt, wenn er durch den tan ersetzt wird, yn durch (n 1) π. Damit wird:
(156) 10-k > 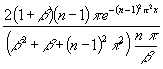 =
= 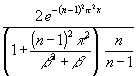 <
< ![]()
Durch Logarithmierung wird daraus:
(157) - k ln 10 > ln 2 (n 1)2 π2 x ==> (n 1)2 π2 x > ln 2 + k ln 10 oder
(158) n > 1 + ![]()
k ln 10 habe ich zu 24 gewählt, d. h. k etwa 8. Die Rechenungenauigkeit muß noch genauer sein, bei 106 Gliedern etwa 103 mal besser. D.h. etwa 10-11. Durch Wahl des entsprechenden Variablentyps erfüllen das die meisten Programme.
6.4 Iteration bei idealer Dämmung
Aus (115) folgt:
(159) ![]()
![]() oder
oder![]()

Vorstehende Gleichung hat auch wieder ∞ viele Lösungen. Zur Iteration wird wieder die rechte Gleichung benutzt in der Form:
(160) 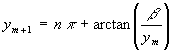
und die Konvergenz ist wie bei Abschnitt 6.1:
(161) 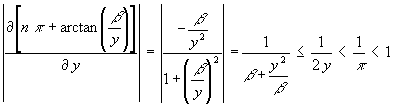
Startwert für jede Iteration ist:
(162) yStart = n π + 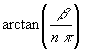
![]() mit
mit![]() n = 1, 2, 3, .. ∞
n = 1, 2, 3, .. ∞
Der Fall n = 0 erfordert eine Sonderbehandlung. Etwa für β > 2,5 ist (160) anwendbar und konvergiert hinreichend. Allerdings wird ein anderer Startwert gebraucht:
(163) yStart = ![]()
![]() für
für![]() n = 0 und β > 2,5
n = 0 und β > 2,5
Für β < 2,5 konvergiert (160) immer noch, aber so schlecht, daß auf das Newtonsche Näherungsverfahren zurückgegriffen wird. Aus (159) folgt:
(164) f(y) = y tan y - β ![]() f ´(y) = tan y + y(1 + tan2y)
f ´(y) = tan y + y(1 + tan2y)![]() f ´´(y) = (1 + y tan y)2(1 + tan2y)
f ´´(y) = (1 + y tan y)2(1 + tan2y)
Bedingung für die Konvergenz des Newton-Verfahrens ist, das f(y) und f ´´(y) das gleiche Vorzeichen haben. Da f ´´(y) immer > 0 ist, muß der Startwert garantieren, daß f (y) > 0 ist. Das ist mit (163) nicht der Fall, deswegen wird ein neuer Startwert gebraucht:
(165) yStart = ![]()
![]() für
für![]() n = 0 und β < 2,5
n = 0 und β < 2,5
Zur Abschätzung bis zu welchen Glied die Reihe berechnet werden muß, wird von (119) ausgegangen. Das nte Glied soll < 10-k sein. Damit entsteht:
(166) 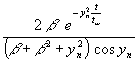 < 10-k
< 10-k
Zur Abschätzung wird bei yn von den Startwerten (162) ausgegangen. Der wird nach unten abgeschätzt, wenn er durch den tan ersetzt wird, yn durch n π. Damit wird:
(167) 10-k > 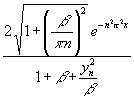 <
< ![]()
Durch Logarithmierung wird daraus:
(168) - k ln 10 > ln 2 n2 π2 x ==> n2 π2 x > ln 2 + k ln 10 oder
(169) n > ![]()
k ln 10 habe ich zu 24 gewählt, d. h. k etwa 8.
Damit sind alle Voraussetzungen geschaffen, um die gesuchten Funktionen zu bestimmen.
*************** nach Gleichung (24) *************************************
Function Heiz(ar, be As Double) As Double 'Heizfaktor bei Strahleinschaltung
Dim zwi, co, si, ch, sh As Double
zwi = 2 * ar
co = Cos(zwi) * Exp(-zwi)
si = Sin(zwi) * Exp(-zwi)
zwi = -2 * zwi
ch = (1 + Exp(zwi)) / 2 'Coshyp(2 * ar)*exp(-2 * ar)
sh = (1 - Exp(zwi)) / 2 'sinhyp(2 * ar)*exp(-2 * ar)
zwi = 1 / Sqr((ch + co) / 2 + be * (sh - si) / 2 + be * be * (ch - co) / 4)
Heiz = zwi
End Function
*************** nach Gleichung (31) *************************************
Function Zeith(ar, be As Double) As Double 'Zeitdifferenz Heiz bei Strahleinschaltung
Dim zwz, zwn, co, si, ch, sh As Double
co = Cos(ar)
si = Sin(ar)
ep = Exp(-ar)
ch = (Exp(ar) + ep) / 2 'Coshyp
sh = (Exp(ar) - ep) / 2 'Sinhyp
zwz = be * sh / 2 + si * ep * (be * (sh - co) / 2 + co)
zwn = ch + be * sh / 2 + sh * ep * (be * (si + co) / 2 - si)
zwz = -Atn(zwz / zwn) * 3.82
Zeith = zwz
End Function
*************** nach Gleichung (38) *************************************
Function Temp(ar, be As Double) As Double 'Temperaturfaktor bei Strahleinschaltung
Dim zwi, co, si, ch, sh As Double
zwi = 2 * ar
co = Cos(zwi) * Exp(-zwi)
si = Sin(zwi) * Exp(-zwi)
zwi = -2 * zwi
ch = (1 + Exp(zwi)) / 2 'Coshyp(2 * ar)*exp(-2 * ar)
sh = (1 - Exp(zwi)) / 2 'sinhyp(2 * ar)*exp(-2 * ar)
zwi = 1 / Sqr((ch + co) / 2 + (sh - si) / be + (ch - co) / (be * be))
Temp = zwi
End Function
*************** nach Gleichung (44) *************************************
Function Temph(ar, be As Double) As Double 'Zeitdifferenz Temp bei Strahleinschaltung
Dim zwz, zwn, co, si, ch, sh As Double
co = Cos(ar)
si = Sin(ar)
ep = Exp(-ar)
ch = (Exp(ar) + ep) / 2 'Coshyp
sh = (Exp(ar) - ep) / 2 'Sinhyp
zwz = sh + si * ep * (si + (1 - be) * co)
zwn = sh + be * ch - si * si * ep
zwz = Atn(zwz / zwn) * 3.82
Temph = zwz
End Function
*************************************
*************** nach Gleichung (61) *************************************
Function HTemp(ar As Double) As Double 'Heizfaktor bei Temperatureinschaltung
Dim zwi, co, si, ch, sh As Double
zwi = ar + ar
co = Cos(zwi)
ex = Exp(-zwi)
zwi = 2 / Sqr((1 + ex * ex) / 2 - ex * co)
HTemp = zwi
End Function
*************** nach Gleichung (72) *************************************
Function TTemp(ar As Double) As Double 'Tempfaktor bei Temperatureinschaltung
Dim zwi, co, si, ch, sh As Double
zwi = ar + ar
co = Cos(zwi)
ex = Exp(-zwi)
zwi = 2 / Sqr((1 + ex * ex) / 2 + ex * co)
TTemp = zwi
End Function
*************** nach Gleichung (66) *************************************
Function Teth(ar As Double) As Double 'Heizzeitdifferenz bei Temperatureinschaltung
Dim zwi, zwz, zwn, co, si, ex As Double
zwi = ar + ar
co = Cos(zwi)
si = Sin(zwi)
ex = Exp(-zwi)
zwz = 1 - ex * (co + si)
zwn = 1 - ex * (co - si)
zwz = -Atn(zwz / zwn) * 3.82
Teth = zwz
End Function
*************** nach Gleichung (77) *************************************
Function Tett(ar As Double) As Double 'Tempzeitdifferenz bei Temperatureinschaltung
Dim zwi, zwz, zwn, co, si, ex As Double
zwi = ar + ar
co = Cos(ar)
si = Sin(zwi)
ex = Exp(-zwi)
zwz = ex * si
zwn = 1 + ex * co * co
zwz = -Atn(zwz / zwn) * 3.82
Tett = zwz
End Function
*************************************
*************************************
'allgemeine Werte
Const pi = 3.14159265358979 ' Wert von Pi
Const Umfang = 10000 ' maximale Feldgröße
Public Art As Integer ' merken welches Koeffizientenfeld
Public Lang As Long ' aktuelle Feldlänge
Public Koff(Umfang) As Double ' Öffentliches Feld - konstanten
Public Zeit(Umfang) As Double ' Öffentliches Feld - Zeitkonstanten
Public koh, kot As Double
*************************************
*************** nach Gleichung (106) *************************************
Function Heiz(aa As Double, ab As Double) As Double 'Heizfunktionswert berechnen
Dim v, grenz As Long
Dim su As Double
If aa = 0 Then
su = 0
Else
If Art <> 1 Then Call Heizko(aa, ab)
If koh <> ab Then Call Heizko(aa, ab)
grenz = 19 + CLng(Sqr((24 + Log(2)) / aa) / pi)
If grenz > Lang Then Call Heizko(aa, ab)
su = 1
For v = 1 To grenz
su = su - Koff(v) * Exp(Zeit(v) * aa)
Next v
End If
Heiz = su
End Function
*************************************
Sub Heizko(hil, Beta As Double) 'Koeffizientensatz berechnen
Dim v As Long
Dim Nulw, hit As Double
Dim Mldg, Stil, Titel, Antwort, Text1
grenz = 20 + CLng(Sqr((24 + Log(2)) / hil) / pi)
If grenz > Umfang Then
Mldg = "Argument zu klein und nicht 0" ' Meldung definieren.
Stil = vbCritical ' Schaltflächen definieren.
Titel = "Programmeinschränkung" ' Titel definieren.
Antwort = MsgBox(Mldg, Stil, Titel) ' Meldung anzeigen.
End If
Lang = grenz
hit = CDbl(Beta)
For v = 1 To grenz
Nulw = Nurh(v, hit)
Zeit(v) = -Nulw * Nulw
Koff(v) = 2 * Nulw * (1 + Beta) / ((Beta * Beta + Beta + Nulw * Nulw) * Sin(Nulw))
Next v
koh = Beta
Art = 1
End Sub
*************************************
Function Nurh(n As Long, ko As Double) As Double 'einzelne Koeff. berechnen
Dim lauf, zwi As Double
Dim s As Integer
zwi = n * pi
If ko = 0 Then
lauf = zwi - pi / 2
Else
lauf = zwi - Atn(zwi / ko)
For s = 1 To 20
lauf = zwi - Atn(lauf / ko)
Next s
End If
Nurh = lauf
End Function
*************************************
*************** nach Gleichung (119) *************************************
Function Temp(aa As Double, ab As Double) As Double 'Funktionswert berechnen
Dim v, grenz As Long
Dim su As Double
If (aa = 0) Or (ab = 0) Then
su = 0
Else
If Art <> 2 Then Call Tempko(aa, ab)
If koh <> ab Then Call Tempko(aa, ab)
grenz = 30 + CLng(Sqr((24 + Log(2)) / aa) / pi)
If grenz > Lang Then Call Tempko(aa, ab)
su = 1
For v = 0 To grenz
su = su - Koff(v) * Exp(Zeit(v) * aa)
Next v
End If
Temp = su
End Function
*************************************
Sub Tempko(hil, Beta As Double) 'Koeffientensatz berechnen
Dim v As Long
Dim Nulw, hit As Double
Dim Mldg, Stil, Titel, Antwort, Text1
grenz = 31 + CLng(Sqr((24 + Log(2)) / hil) / pi)
If grenz > Umfang Then
Mldg = "Argument zu klein und nicht 0" ' Meldung definieren.
Stil = vbCritical ' Schaltflächen definieren.
Titel = "Programmeinschränkung" ' Titel definieren.
Antwort = MsgBox(Mldg, Stil, Titel) ' Meldung anzeigen.
End If
Lang = grenz
hit = CDbl(Beta)
Nullko (hit)
For v = 1 To grenz
Nulw = Nurt(v, hit)
Zeit(v) = -Nulw * Nulw
Koff(v) = 2 * Beta / ((Beta * Beta + Beta + Nulw * Nulw) * Cos(Nulw))
Next v
koh = Beta
Art = 2
End Sub
*************************************
Function Nurt(n As Long, ko As Double) As Double 'einzelne Koeff. berechnen
Dim lauf, zwi, zwia As Double
Dim s As Integer
zwi = n * pi
lauf = zwi + Atn(ko / zwi)
For s = 1 To 20
lauf = zwi + Atn(ko / lauf)
Next s
Nurt = lauf
End Function
*************************************
Sub Nullko(ko As Double) 'nullten Koeff. berechnen
Dim lauf, zwi, zwia As Double
Dim s As Integer
lauf = Sqr(ko)
If ko > 3 Then
lauf = Atn(lauf)
For s = 1 To 20
lauf = Atn(ko / lauf)
Next s
Else
For s = 1 To 20
zwia = Tan(lauf)
zwi = lauf * zwia - ko
zwia = zwia + lauf * (1 + zwia * zwia)
lauf = lauf - zwi / zwia
Next s
End If
Zeit(0) = -lauf * lauf
Koff(0) = 2 * ko / ((ko * ko + ko + lauf * lauf) * Cos(lauf))
End Sub
*************************************
*************** nach Gleichung (140) *************************************
Function HTemp(aa As Double) As Double 'Heizwert bei Temperatureinschaltung
Dim v, grenz As Long
Dim su, kof As Double
Const piq = -pi * pi
If aa = 0 Then
su = 0
Else
grenz = 20 + CLng(Sqr((24 + Log(2)) / aa) / pi)
su = 1
For v = 1 To grenz
kof = v / 2 - CInt(v / 2 - 0.25)
If kof > 0.25 Then kof = 2 Else kof = -2
su = su - kof * Exp(v * v * piq * aa)
Next v
End If
HTemp = su
End Function
*************** nach Gleichung (149) *************************************
Function TTemp(aa As Double) As Double 'Temperaturwert bei Temperatureinschaltung
Dim v, grenz As Long
Dim su, kof As Double
Const piq = -pi * pi
If aa = 0 Then
su = 0
Else
grenz = 40 + CLng(Sqr((24 + Log(2)) / aa) / pi)
su = 1
For v = 1 To grenz
kof = v / 2 - CInt(v / 2 - 0.25)
If kof > 0.25 Then kof = 4 / pi Else kof = -4 / pi
su = su - kof * Exp((v - 0.5) * (v - 0.5) * piq * aa) / (v + v - 1)
Next v
End If
TTemp = su
End Function
*************************************
Für die Diagrammdarstellung der berechneten Kurven werden 2 Materialien, deren Daten in [1] angegeben sind, ausgewählt. Bei einem Wertebereich ist der Mittelwert genommen. Für ε wird der Wert aus [4] genommen:
Material |
λ |
a |
b |
W/m K |
10-7 m2/s |
Ws½/(K m2) |
|
Kiesbeton |
1,280 |
6,62 |
1570 |
Styropor |
0,037 |
9,50 |
49 |
Der Verlustfaktor wird mit ε = 4,12 W/( K m2) [4] angesetzt.
Als Periodendauer wird der Tag, d.h. 24 Stunden genommen. Im Bogenmaß ausgedrückt ist dann die Zeitverzögerung Δ t = φ 24 h/ 2 π ==> Δ t = φ 3,82 h. Im Winkelmaß ausgedrückt ist dann die Zeitverzögerung Δt = φ 24 h/ 360° ==> Δt = φ 0,0667 h.
Material |
1/κ |
α |
H(∞) |
Δq/h |
S(∞) |
ΔT/h |
m |
||||||
Kiesbeton |
0,13 |
0,42 |
1,63 |
0,66 |
0,48 |
2,34 |
Styropor |
0,16 |
17,80 |
0,15 |
2,79 |
1,89 |
0,20 |
Bild 1: Materialfaktor nach (24), (38), (61) bzw. (72)
Bild 2: Nenner Abschwächung nach (21), (35), (58) bzw. (69)
Bild 3: vergrößert Anfang von Bild 2 für kleine Werte
Bild 4: Zeitdifferenz nach (30), (44), (66) bzw. (77)
Bild 5: Zeitverzögerung nach (26), (40), (63) bzw. (74)
Bild 6: vergrößert Anfang von Bild 5 für kleine Werte
Material |
w0/m |
tN/s |
tN/h |
Kiesbeton |
0,3100 |
145200 |
40,330 |
Styropor |
0,0089 |
141 |
0,039 |
Bild 7: Heizverlauf nach Einschalten nach (106) (Parameter β), (140): TH
Bild 8: vergrößert Anfang von Bild 7 für kleine Werte
Bild 9: Temperaturverlauf nach Einschalten (119) (Parameter β), (149): TT
Bild 10: vergrößert Anfang von Bild 9 für kleine Werte
| [1] | Grigull, U.; Sandner, H.: | Wärmeleitung. Springer-Verlag Berlin Heidelberg New York 1979 |
| [2] | Heindl, W.: | Der Wärmeschutz einer ebenen Wand bei periodischen Wärmebelastungen. Die Ziegelindustrie, 1966 H. 18, S. 685 - 693, 1967 H. 1, S. 1 - 8, H. 18, S. 593 - 599 |
| [3] | Ebel, J.: | Wie steht es mit der Anwendbarkeit des u-Wertes? http://www.Ing-Buero-Ebel.de/Arbeiten/UWert/UWert.htm |
| [4] | Ebel, J.: | Oberfläche und Speicherung. http://www.Ing-Buero-Ebel.de/Arbeiten/Wand/OberflaecheL.htm |
| [5] | Nehring, G.: | Über den Wärmefluß durch Außenwände und Dächer in klimatisierte Räume infolge der periodischen Tagesgänge der bestimmenden meteorologischen Elemente. Gesundheits-Ingenieur 83 (1962) H. 7, S. 185 - 189; H. 8, S. 230 - 242; H. 9, S. 253 - 269 |
| [6] | Bronstein, I. N.; Semendjajew, K. A.: |
Taschenbuch der Mathematik. BSB B.G. Teubner Verlagsgesellschaft, Leipzig 1979 |
| [7] | Smirnow, W. L.: | Lehrgang der höheren Mathematik Teil III/2. VEB Deutscher Verlag der Wissenschaften. Berlin 1961 |
| [8] | Oberhettinger, F.; Badii, L.: | Tables of Laplace Transforms. Springer-Verlag. Berlin Heidelberg New York 1973 |
| [9] | YTONG: | Planungsunterlagen Wohnungsbau 1999 |
| [10] | Fischer, K. u.a.: | Dämmstoffe im Rotlicht - Ein Meßexperiment. http://konrad-fischer.bei.t-online.de/213baust.htm - oder - Temperaturmessung - Dämmstoffe im Vergleich. B+B Bautenschutz und Bausanierung 24(2001) H. 8, S. 9 |