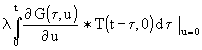
Dipl.-Physiker Jochen Ebel

Oberfläche und Speicherung

1. Aufstellung der Gleichungen

3. Darstellung der normierten Temperaturfunktion

4. Schlußfolgerungen
5. Literatur

1. Aufstellung der Gleichungen

In [1] wurde nachgewiesen, daß der Zeitverlauf der Oberflächentemperatur allein bestimmend ist für die Wärmespeicherung in der Wand bei gegebenen Aufbau. Offen geblieben ist die Frage nach dem Zusammenhang zwischen Oberflächentemperatur und den Umgebungsbedingungen. Das Problem kann hier nur für wenige Spezialfälle gelöst werden, aber damit kann für viele Fälle der Einfluß abgeschätzt werden.

Eine wichtige Rolle dabei spielt der Begriff des Gleichgewichtes. Wenn sich die Umgebungsbedingungen laufend ändern, ist es schwer bis unmöglich, den momentanen Abstand zum Gleichgewicht zu bestimmen. Deswegen wird der hier nur ein Spezialfall untersucht: In einer Umgebung, die für alle Zeiten eine Temperatur von 0°C hat, befindet sich eine ∞ dicke Wand, die für die Zeit t < 0 auch die Temperatur 0°C hat, ab der Zeit t = 0 soll eine konstante Strahlung mit dem nichtreflektierten Anteil E einfallen. Dieser hat in SI-Einheiten die Dimension W/m².

Gesucht wird die Oberflächentemperatur der Wand. Dabei ist zu berücksichtigen, daß es bei steigender Wandtemperatur T zum Wärmeverlust in die Umgebung kommt. Für Zeiten < 0 sollte ja Gleichgewicht herrschen, d.h. abgestrahlte und empfangene Wärmestrahlung waren gleich. Ohne wesentliche Einschränkung der Allgemeinheit wird angenommen, daß der bei Temperaturerhöhung eintretende Wärmeverlust proportional der Temperatur ist (siehe Gleichung (97) und (98)). Damit wird ein Verlustkoeffizient ε (mit etwas anderer Bedeutung gleich dem Wärmeübergangskoeffizienten) definiert, der nur von der Art der Oberfläche abhängig ist, aber unabhängig vom weiteren Aufbau der Wand (siehe z.B. [4]). Dieser hat in SI-Einheiten die Dimension W/(m²K). Der Wärmestrom im Wandinnern wird q genannt. Dieser hat in SI-Einheiten die Dimension W/m². Aus der Definition der Wärmestromrichtung in [1] ist für q ein "-" zu berücksichtigen. Damit entsteht folgende Gleichung:

(1) E - ε T = -q

Bei [1, Gl. (17)] ergibt sich bei Berücksichtigung der Voraussetzung, das T(t) für t<0 gleich 0 sein soll, daß die obere Integrationsgrenze nicht bis ∞, sondern nur bis t reicht. Mit der modifizierten [1, Gl. (17)] ergibt sich aus (1):

(2) E - ε T(t,0) = -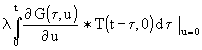

Wegen der vorausgesetzten dicken Wand ist aus [1, Gl. (16)] auch die Funktion G bekannt. Dabei hat a in SI-Einheiten die Dimension m²/s (als Ortskoordinate wird u verwandt zum Unterschied von x, daß späteren als normierte Zeit genommen wird):

(3) 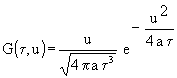mit

(2) und (3) ist eine Volterragleichung 2. Art [5, S. 4ff] zur Bestimmung der unbekannten Funktion T.

1.1 Anwendung der Laplace-Transformation

Vorstehende Aufgabe wird zweckmäßig mit der Laplacetransformation behandelt, siehe [2] oder [3, S. 94ff]. Zunächst wird (3) transformiert. Dafür ist keine Bildfunktion in der Tabelle [2, S. 139ff] vorhanden. Unter Nr. 52 ist ein Transformationspaar aufgeführt, Mit dem weitergearbeitet werden kann:

(4)

Durch Differentation nach dem Parameter α geht (4) in (5) über, die in (3) hilft:

(5)

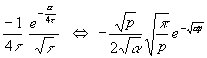
Im Transformationspaar wird noch – 4 multipliziert, τ links mit unter die Wurzel genommen und rechts gekürzt. Damit entsteht:

(6)

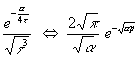
Wird (3) mit (6) verglichen, ergibt sich:

(7) α =

Und für die ganze Transformation:

(8)

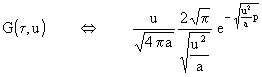
Obige Gleichung läßt sich durch Kürzen usw. in eine bessere Form bringen:

(9)

Gebraucht wird aber nicht G selber, sondern die Ableitung nach x (im Sinne der Laplacetransformation nach dem Parameter x):

(10)

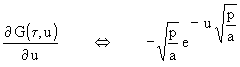
Mit dem Faltungssatz der Laplacetransformation und der Laplacetransformierten der Konstante E wird aus (2) mit (9):

(11) - ε T_L(t,0) =

In (11) wird noch berücksichtigt, daß der Wärmestrom an der Stelle u = 0 betrachtet wird, dadurch wird die e-Funktion zu 1 und braucht nicht aufgeführt zu werden:

(12) - ε T_L =

(12) hat die Form einer algebraischen Gleichung und wird nach T_L aufgelöst:

(13) T_L = E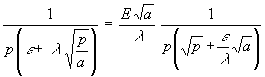

Verschiedene Konstanten lassen sich zum Wärmeeindringkoeffizienten b zusammenfassen [3]. Dabei hat b in SI-Einheiten die Dimension Ws^½/m²K:

(14) b =

Mit (14) wird aus (12):

(15) T_L =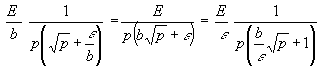

Zunächst aus Dimensionsgründen wird folgende Zeit t_N definiert, aber später zeigt sich, daß das eine sehr gute Vergleichszeit ist:

(16)

Damit wird aus (15):

(17) T_L =

Zur späteren Verwendung werden verschiedene Größen eingeführt:

(17-1) T_E =

Zum einfachen Auswerten werden normierte Größen benutzt:

(17-2) x = t = t_N × x

(17-3) y = T_L = T_E × y

2. Lösung der Gleichung

2.1 Rücktransformation

2.1.1 Rücktransformation mit Tabelle

Am Einfachsten ist die Rücktransformation durch Rückgriff auf eine Tabellensammlung. Wegen der Wurzel im Nenner ist dieses Transformationspaar nur in umfangreichen Sammlungen zu finden, z.B. [7]. In [7, S. 229] ist unter Nr. 3.22 das gesuchte Transformationspaar zu finden:

(18) mit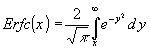

Allerdings ist in [7] ein Druckfehler (das "e" wurde vergessen), so daß noch eine Überprüfung stattfinden muß, ob (18) richtig ist.

2.1.2 Überprüfung durch Reihenvergleich

Dazu wird zunächst (18) mit a, das hier nach Vergleich mit (17) den Wert hat multipliziert, so daß:

(19) 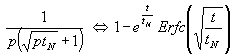mit

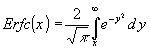
entsteht. Mit (19) folgt aus (17):

(20) T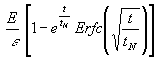(t) = mit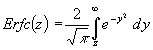

Mit der Normierung (65) wird aus (20):

(21) y(x) = mit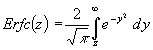

Zusammengefaßt wird:

(22) y(x) =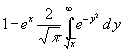

Für Erfc(x) wird noch eine andere Darstellung gewählt:

(23)

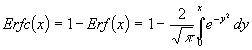
Zunächst wird in (23) der Integrand (die e-Funktion) als Potenzreihe dargestellt und gliedweise integriert. Dann wird auch in (22) die e-Funktion als Potenzreihe dargestellt. Damit sind alle Ausdrücke in (22) als Potenzreihe vorhanden. Die beiden Potenzreihen werden miteinander multipliziert und das Ergebnis gliedweise mit Abschnitt 2.5 vergleichen. Das Ergebnis zeigt, es ist richtig.

2.1.3 Überprüfung durch Transformation

Eine 2. Möglichkeit der Überprüfung ist die Transformation von (19). Dazu wird von der Definition der Laplace-Transformation ausgegangen:

(24) f(p) =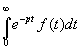

In (24) wird (19) eingesetzt:

(25) f(p) =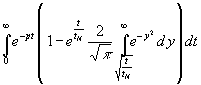

Die Integration ist nun auszuführen. Zuerst wird die 1 integriert (dabei ist –pt zu substituieren):

(26) f₁(p) =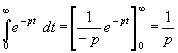

Danach wird der Rest integriert durch partielle Integration, aber zuerst im inneren Integral die Integrationsgrenzen umgetauscht (Vorzeichenwechsel dabei beachten):

(27) f₂(p) =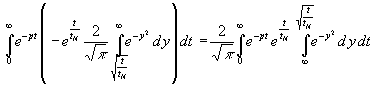

f₂(p) =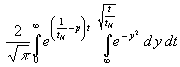

Bei Differentation des inneren Integranden (Teil der partiellen Integration) entfällt das Integral, im Integranden ist die Grenze einzusetzen und die Integrationsgrenze zu differenzieren:

f₂(p) =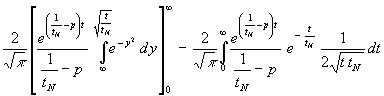

Der erste Term ist bekannt, da im Integral die obere Integrationsgrenze zu 0 bzw. ∞ wird. Dabei ist der Wert an der oberen Grenze (∞) 0. An der unteren Grenze (0) ist die Exponentialfunktion = 1 und das Integral hat den Wert ([6, S. 118, Nr. 3], umgedrehte Integrationsgrenzen beachten). Im zweiten Term werden einige elementare Umformungen gemacht. Damit wird:

f₂(p) =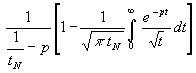

Dabei war das Integral wieder bekannt [6, S. 117, Nr. 1] mit n = - ½ und Γ(½) = [6, S. 155] als :

f₂(p) =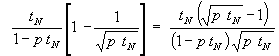

Da (p t_N - 1) = ( - 1)( + 1) ist, wird aus obiger Gleichung durch Kürzen:

(28) f₂(p) =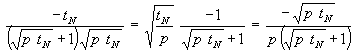

Mit (26) und (28) wird aus (25):

(29) f(p) = f₁(p) + f₂(p) =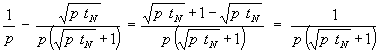

Der Vergleich von (19) und (29) zeigt, daß das Transformationspaar richtig ist.

2.2 Reihenentwicklung für große Zeiten

Die Entwicklung geht von der Lösbarkeit des nachfolgenden Integrals aus:

(30)

Mit (30) läßt sich folgendes Integral nach Erweiterung des Integranden mit y/y durch partielle Integration lösen (das Zähler-y wird zur Exponentialfunktion zugehörig genommen):

(31)

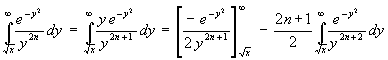
(32)

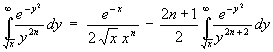
Zweckmäßig wird (32) noch mit erweitert, so wird:

(33)

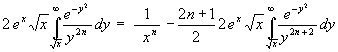
Aus (22) wird durch fortgesetzte Anwendung von (33) eine Reihenentwicklung (das erhaltene Integral ist jeweils wieder ein Integral vom Typ (31), da (33) für n = 0 das Integral in (22) ist):

(34) y(x) =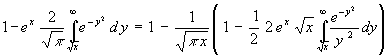

(35) y(x) =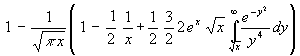

(36) y(x) =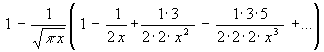

Allgemein kann man das n_te Glied angeben:

(37) G(n) = 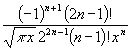für n = 1, 2, ... und G(0) =

Da (36) eine alternierende Reihe ist, ist der Fehler bei Abbruch der Reihe immer kleiner als das erste weggelassene Glied. Die Reihe wird aber nicht um so genauer, um so mehr Glieder man nimmt. Nach einem Minimalbetrag an einer Stelle der Reihe steigen die Glieder wegen einer Art Fakultät im Zähler. Zur Abschätzung des Restgliedes gehe ich noch einmal von (33) aus mit einer Substitution y = + u und elementaren Umformungen:

(38)

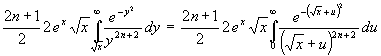
(39)

Da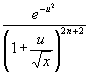< 1 für alle u > 0 wird, wird das Integral nur vergrößert, wenn dieser Faktor weggelassen wird. Damit ist das folgende Integral zu lösen:

(40)

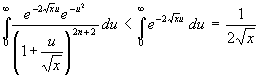
Mit (40) wird aus (39) mit = 1:

(41)

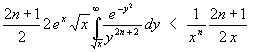
Die Gleichung (41) legt nahe, als letztes Glied nur die Hälfte des Reihengliedes zu nehmen. Der Fehler ist dann maximal gleich diesem Glied.

(42) Fehler < =

Mit der Stirlingschen Formel für große Fakultäten [6, S. 155] kann (42) noch vereinfacht werden:

(43) Fehler <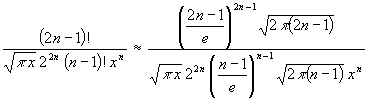

Durch Kürzen und Herausziehen von Faktoren wird:

(44) Fehler <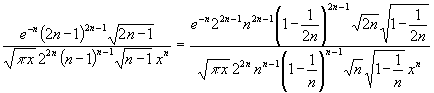

Da 1/2n < 1/n wird beim Weglassen der Brüche in den einzelnen Ausdrücken die Fehlerschranke höchstens vergrößert:

(45) Fehler <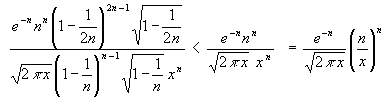

Damit das minimale Glied nicht überschritten wird, folgt aus (35) und (41):

(46)

Wird (46) in (45) eingesetzt, erhält man:

(47) Fehler <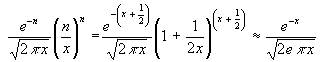

Für x > 10 ist deshalb der Fehler < 3 • 10^-6. Bei großen x wird n unnötig groß. Soll beispielsweise der Fehler < 10^-7 sein, so gilt mit (45):

(48) 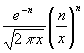< 10^-7

Für x > 14 folgt etwa n > 14, für n > 20 folgt etwa n > 6. Daraus folgt, das es immer reicht 14 Glieder zu nehmen. Oder man nimmt immer 14 Glieder und fängt wegen (46) erst bei x > 14 mit der Verwendung dieser Reihe an.

2.3 Reihenentwicklung für kleine Zeiten

Aus (21) bis(23) folgt:

(49) y(x) =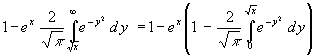

Von den e-Funktionen wird nur das 0_te Glied genommen ( = 1). Damit ist nur eine Konstante zu integrieren. Somit wird aus (49):

(50) y(x) =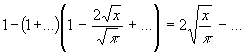

Die weitere Entwicklung ist in Abschnitt 2.5.

2.4 Asymptotische Lösung

In Abschnitt 2.1 ist (17) zurück transformiert worden. Obwohl (17) einfach aussieht, ist – wie schon erwähnt – wegen der Wurzel die Rücktransformation nur in größeren Tabellenwerken zu finden. Als Beispiel für das Vorgehen bei weniger umfangreichen Tafelwerken wird eine Funktion T_K konstruiert, die für t0 und t asymptotisch gleich der richtigen unbekannten Funktion ist. Zunächst sind die Asymptoten zu konstruieren [2, S. 42]. Für t0 wird als Vergleichsfkt. die Fkt. genommen. Nach [2, S. 139ff] wird mit Nr. 41:

(51) T(t0) =

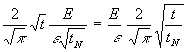
Für t ∞ ist

(52)

Vergleicht man (17) mit (1) für q0 (bei t∞), so folgt:

(53) T(t ∞) =

(51) und (53) legen folgende Funktion für T_K nahe:

(54) T_K(t) =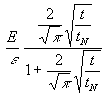

Für t ∞ werden Zähler und Nenner fast gleich, d.h. der Bruch wird 1. Damit wird (53) asymptotisch erfüllt.. Für t0 wird in (54) der Nenner zu 1, damit wird (51) erfüllt. Mit der Normierung (65) wird aus (54):

(55) y_K(x) =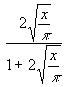

Da aus Abschnitt 2.2 auch die Entwicklung von y(x) für große x bekannt ist, wird (55) so modifiziert, das für große x nicht nur die 0_te Näherung ( = 1), sondern auch die 1. Näherung erfüllt wird. Zur Anpassung wird ein wählbarer Parameter α eingeführt:

(56) y_K(x) =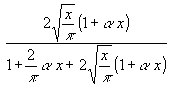

Wie man sich durch Ausrechnen überzeugen kann, erfüllt (56) für alle α nicht nur die 0. sondern auch die 1. Näherung für x ∞. Durch α wird der Übergang von der Klein-x-Näherung zur Groß-x-Näherung beeinflußt. Wie später ausgeführt wird, ist ein Wert von ≅ 0.69 optimal und hält den maximalen Differenzfehler zwischen exaktem und Näherungs-Wert unter 0,011.

2.5 Gewichtsfunktion und Lösung mit Reihen

2.5.1 Gewichtsfunktion und Lösungsansatz

Die Gleichung (21) ist so beschaffen, das nur wenige Tabellenwerke diese Funktion tabelliert haben und auch diese wurden im allgemeinen durch Reihenentwicklung berechnet. Das ist auch bei anderen – selbst einfachen Funktionen wie Integralsinus – bekannt. Für große x ist die Reihenentwicklung schon Abschnitt 2.2 durchgeführt. Für kleine x ist der Weg über Abschnitt 2.3 sehr umfangreich. Deshalb wird hier ein anderer Weg gegangen.

Wird in (15) im Fall ε = 0 betrachtet, so entsteht:

(57) T_L =

Dafür existiert in [2, S. 139ff] die exakte Lösung der Rücktransformation mit Nr. 41:

(58) T(t) =

Hier wird wieder eine Gewichtsfunktion J(τ) eingeführt, denn die Temperatur zu einem beliebigen Zeitpunkt hängt von den Wärmeströmen in die Wand von der Zeit davor ab:

(59) T(t) =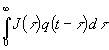

Hat q(t - τ) die spezielle Form der Einschaltfkt. wie in Abschnitt 1 genannt (für t < 0: q = 0 und für t > 0 konstant E), so nimmt (59) die Form

(60) T(t) =

Da im Integranden t nicht mehr enthalten ist, wird die Gewichtsfunktion nach der Rechenregel der Differenzierung von Integralen durch einfaches Differenzieren erhalten:

(61)

Durch Einsetzen von (58) in (61) und Durchführung der Differentation wird erhalten:

(62) J(t) =

Setzt man in (62) die mit (16) definierte Zeit t_N ein, so wird:

(63) J(t) =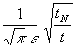

Damit kann (59) weiter ausgewertet werden, indem man (1) (q = die Einstrahlung E vermindert um den Abstrahlungsverlust ε T) und (63) einsetzt:

(64) T(t) =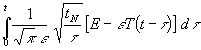

(64) ist eine wie schon in Abschnitt 1 erwähnt eine Volterrasche Integralgleichung 2. Art [5, S. 4ff] zur Bestimmung von T(t). Um die Allgemeinheit deutlicher zu machen, sind 2 Normierungen zweckmäßig:

(65) t = t_N x und T(t) = T(t_N x) =

Mit (65) wird aus (64) nach Kürzen von E und ε (für τ wird dann natürlich τ = t_N u substituiert):

(66) y(x) =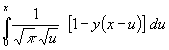

Der erste Term (die 1) in der eckigen Klammer ist einfach zu integrieren (Umkehrung von (61)). Im restlichen Integral wird u = x (1 – v) substituiert. Damit wird (Vertauschung der Integrationsgrenzen nach Substitution beachten):

(67) y(x) =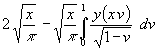

2.5.2 Ansatz und und Lösung der Reihe

Zur Lösung von (67) wird ein Potenzreihenansatz gemacht:

(68) y(x) =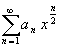

Wird (68) in (67) eingesetzt, entstehen nach Vorziehen der x-Potenzen (erlaubt, da unabhängig von der Integrationsvariablen) vor das Integral Bestimmungsgleichungen für die a_n.

(69) =

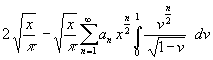
Die Wurzel wird noch mit unter das Summenzeichen gezogen und im letzten Term n+1 = m gesetzt::

(70) =

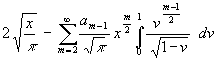
Da (70) für beliebige x erfüllt sein soll, ist das nur möglich, wenn die Koeffizienten von x gleich sind. Damit entsteht (m wird wieder n genannt – der Name eines Indizes ist unwesentlich):

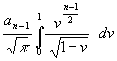(71) a₁ = a_n = - für n = 2 bis ∞

Die Integrale in (71) sind tabelliert [6, S. 122, Integral 39.]. Dabei entsprechen obige Integrale der Tabelle mit α = und β = :

(72)

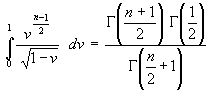
Die Gammafunktionen von ½ ist ([6, S. 155]). Damit wird aus (71):

(73) a_n = - 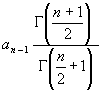für n = 2 bis ∞

Die direkte Auswertung von (73) ist sehr umfangreich. Schreibt man aber (73 ) für m = n-1 auf, so wird:

(74) a_m-1 = - 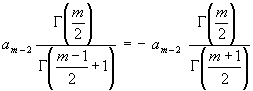für m = 3 bis ∞

Bezeichnet man in (74) wieder m mit n und setzt die erhaltene Gleichung in (73) ein, kürzt eine Gammafunktion (wegen Gleichheit) und wird im Rest die Rekursionsformel der Gammafunktion [6, S. 383, 3.] berücksichtigt, ist eine weitere Gammafunktion zu kürzen. So erhält man:

(75) a_n = für n = 3 bis ∞ mit a₁ = und a₂ = −1 (siehe Gleichung (77))

Für n gerade und ungerade kann man a_n allgemein angeben:

(76) und für m = 1 bis ∞

Aus (73) folgt:

(77) a₂ = - 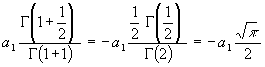= -1

Aus (76) folgt mit (71) und (77):

(78) und für m = 1 bis ∞

Aus (68) wird mit (78), bei Berücksichtigung, daß für ungerade Glieder a auch bei m = 0 richtig ist und die Reihe für die geraden Glieder bei Hinzufügen des 0. Gliedes (das natürlich wieder abgezogen werden muß) die Potenzreihenentwicklung der e-Funktion ist :

(79) y(x) = - =

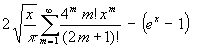
Werden von dieser Reihe nur die ersten 2 Glieder genommen, so wird:

(79a) y(x) ≅ 2− x = 2(1 − )

Für manche Zwecke ist auch noch eine Reihe interessant:

(79b) y^*() = ≅ 1 −

Im nachfolgendem Diagramm sind y(x) und y^*() über mit ihren Näherungen erster Ordnung aufgetragen.

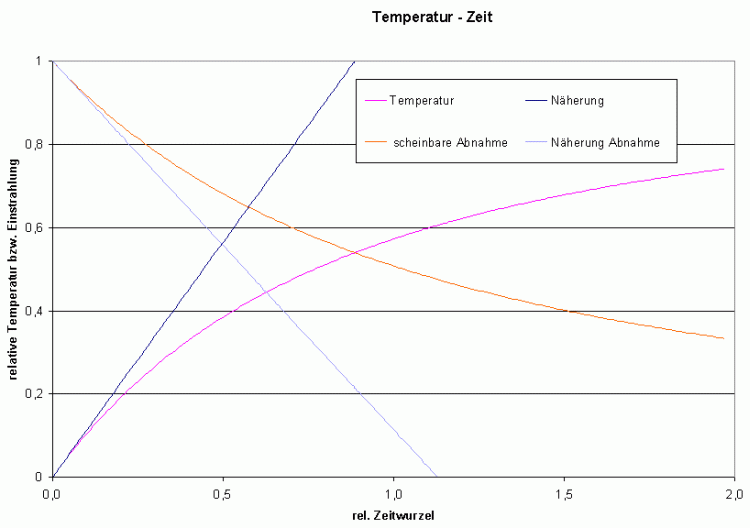
Wird (79a) noch mit (16) und (21) entnormiert, wird daraus:

(79c) T(t) = y() ≅ 2 (1 − ) = 2 E b(1 − )

2.5.3 Fehlergrenzen der Reihe

Die beiden Reihen in (79) konvergieren unterschiedlich schnell, aber monoton. Durch den Abbruch der Reihe entsteht ein Fehler. Der soll zuerst für die zweite Summe bestimmt werden. Dazu wird zuerst die Summe auf 2 Teilsummen aufgeteilt:

(80) = + = +

In der letzten Summe führe ich einen neuen Index v = m – (n+1) ein:

(81) = +

Die rechte Seite wird höchstens vergrößert, wenn in der Nennerfakultät der letzten Summe alle Faktoren größer n + 1 durch n + 1 ersetzt werden, da jedes einzelne Glied vergrößert wird, wegen Verkleinerung des Nenners. Damit wird:

(82) < + = +

Jetzt stellt die letzte Summe eine geometrische Reihe dar, die konvergiert, wenn der Bruch < 1 ist. Mit der Summenformel der geometrischen Reihe:

(83) wenn a < 1

wird:

(84) < + = +

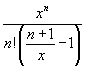
Wenn

(85) n + 1 > 2 x

dann ist der Abbruchfehler der Reihe höchstens so groß wie das letzte verwendete Glied. Dabei kann das letzte Glied aber noch sehr groß sein. Deswegen wird besser gewählt:

(86) n > 4 x

Mit der Stirlingschen Formel und (86) wird das Fehlerglied weiter ausgewertet:

(87) Fehler <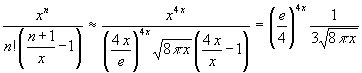

Wenn x < 20 dann wäre der Fehler < 10^-14 wenn keine Rechenungenauigkeiten auftreten würden. Da aber bei großen x auch einzelne Reihenglieder sehr groß werden, beschränkt die Rechengenauigkeit die Größe von x. Um das maximale x zu finden brauche ich den Wert des größten Gliedes. Aus (80) folgt, das die Reihenglieder so lange steigen bis x/m < 1 wird. Deswegen ist das größte Glied bei m ≅ x. D.h. der Wert des maximalen Gliedes ist:

(88) Glieder <

Die weitere Auswertung geschieht wieder mit der Stirlingschen Formel und elementaren Umformungen:

(89) Glieder <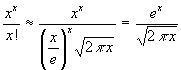

Bei x ≅ 20 ist das etwa 4,3•10⁷, bei x ≅ 10 ist das etwa 2,8•10³. Mit 8 Byte Zahlendarstellung (6 Byte Mantisse) ist die relative Rechenungenauigkeit ≅ 3•10^-15. Mit dem Größtwert 4,3•10⁷ wird die absolute Rechenungenauigkeit ≅ 1,2•10^-7. Diese Rechengenauigkeit wird auch erreicht, so daß bei x ≅ 20 die obere Grenze der Reihenentwicklung für kleine Argumente liegt. Damit überlappen sich die Grenzen der Anwendbarkeit der Reihenentwicklungen für große und für kleine x. Die Berechnung der Werte mit beiden Reihen im Bereich 10 < x < 20 zeigt, das der minimale Rechenfehler bei einer Grenze von etwa 13,5 liegt und der Fehler ≅ 10^-8 ist.

Nun ist noch die erste Summe in (79) zu behandeln. Wenn gezeigt wird, das ab einem bestimmten ungeradem Glied die ungeraden Glieder < die vorhergehenden geraden Glieder (betragsmäßig) sind, dann gilt die Fehlerabschätzung für die geraden Glieder auch für die ungeraden.

(90) < für m > ?

Durch elementare Umformungen folgt aus (90):

(91) < 1 für m > ?

(92) = < 1 für m > ?

Die weitere Auswertung von (92) geschieht wieder mit der Stirlingschen Formel:

(93) = 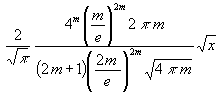< 1 für m > ?

Mit elementaren Umformungen wird daraus:

(94) 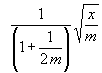< 1 für m > ?

Mit (94) ist die Frage zu beantworten: Für

(95) m > x

sind die Abschätzungen zur Ungenauigkeit der geraden Folgeglieder auch auf die ungeraden zu übernehmen.

3. Darstellung der normierten Temperaturfunktion

3.1 VBA-Basic zur Reihenberechnung

Damit sind nun die Grundlagen geschaffen, damit y und y_K (Gl. (56)) tabelliert und als Diagramm dargestellt werden können. Für große x wird y mit (36) tabelliert, für kleine x aus (68) mit Hilfe von (78). Die Funktionen haben in VBA-Basic z.B. folgendes Programm:

Const pi = 3.141592653589
_________________________
Function Gesamt(wer As Double) As Double 'Berechnung y, Übergabe x als wer
Dim facg, facu, summ As Double
Dim v, grenz As Integer
 
If wer < 13.5 Then 'Trennung große / kleine x
facu = 2 * Sqr(wer / pi)
facg = 1
summ = facu
grenz = Int(wer * 4) + 20
For v = 1 To grenz
facu = facu * 2 * wer / (v + v + 1)
facg = facg * wer / v
summ = summ + facu - facg
Next v
Else 'für große x
facu = 1 / Sqr(wer * pi)
summ = 1 - facu
For v = 0 To 14
facu = -facu * (v + v + 1) / (wer + wer)
summ = summ - facu
Next v
summ = summ + facu / 2
End If
Gesamt = summ 'Übergabe y
End Function
___________________________________________
Function Anpaß(wer As Double, koff As Double) As Double 'Berechnung y_K
Dim bruch As Double
 
bruch = 2 * Sqr(wer / pi) * (1 + koff * wer)
Anpaß = bruch / (1 + 2 * koff * wer / pi + bruch)
End Function

3.2 Diagrammdarstellung

Das Computerprogramm berechnet folgenden Verlauf:

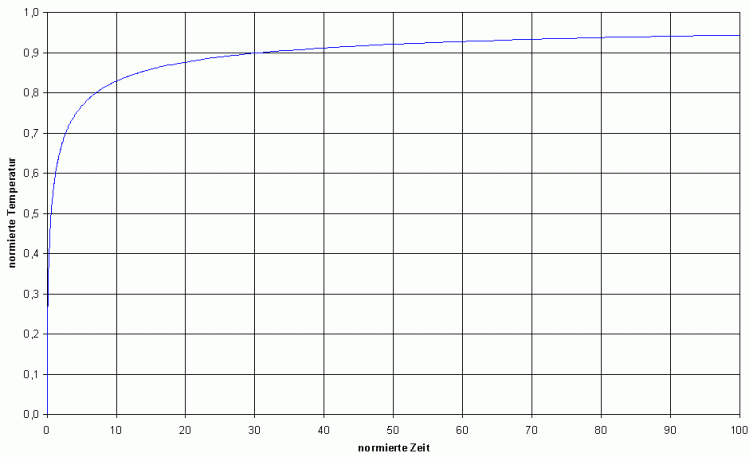
Bild 1: normierter Temperaturverlauf über normierter Zeit

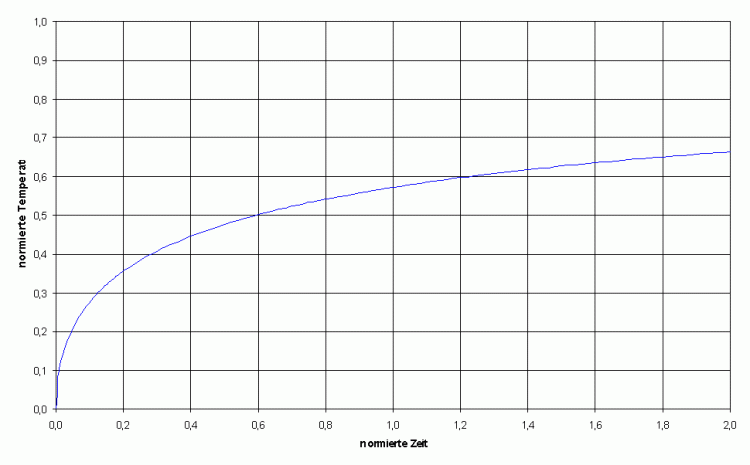
Bild 2: Auszug aus Bild 1 für kleine Zeiten

Bild 3: Differenz zwischen exaktem und Näherungswert bei α = 0,69

In (56) wurde der Koeffizient α so lange variiert, bis der Betrag der maximalen und minimalen Abweichung etwa gleich klein geworden ist. Das war bei α ≅ 0,69 der Fall und ist dargestellt.

4. Schlußfolgerungen

Für Zeiten t << t_N ist der Wärmeleitungsvorgang weit vom Gleichgewicht entfernt, d.h. der Wärmeverlust durch Erhöhung Oberflächentemperatur ist klein gegenüber der Einstrahlung.

Für typische Materialien ist nun t_N zu bestimmen. Zuerst wird ε bestimmt. Wird für ε der schwarze Strahler genommen {mit T_U Umgebungstemperatur, ΔT der Temperaturerhöhung,

(96) σ = 5,67•10^-8 W/(m² K⁴)}

wird die Energieabstrahlung E^*. Dabei muß berücksichtigt werden, das die Oberfläche nicht nur Energie abstrahlt, sondern auch von der Umgebung Energie zugestrahlt bekommt.

Anmerkung: Für den Namen von σ ist "Stefan-Boltzmann-Konstante" am gebräuchlichsten. Daneben gibt es noch den Namen "Stefan-Konstante" [12, Seite 665: "universelle Stefan-Konstante", Seite 862: "Stefan-Boltzmann", Seite 887: beide]. Das ist erklärlich, denn Stefan hat 1879 [9] das T⁴-Gesetzt herausgebracht, Boltzmann hat das 1884 [10] ergänzt. Die DIN [13] nennt keinen Namen .

Im Zustand vor Einschalten der zusätzlichen Strahlungsquelle E (siehe (1)) hatte die Oberfläche genausoviel Energie empfangen, wie sie selbst abgestrahlt hat (Gleichgewicht), d.h. E^* war 0. Deswegen wird zweckmäßig die Temperatur der Oberfläche als Summe von Umgebungstemperatur und Temperaturerhöhung angesetzt:

(97) E^* = σ (T_U + ΔT)⁴ - σ T_U⁴ = σ (4T_U³ ΔT + 6T_U2 ΔT2 + 4T_U ΔT³ + ΔT⁴) = σ 4T_U³ ΔT {1 + }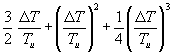

Bei den interessierenden Temperaturdifferenzen sind die Brüche in der geschweiften Klammer so klein gegen 1, das sie vernachlässigt werden können. Daher wird für E^* nur der in ΔT lineare Anteil genommen und mit (1) wird:

(98) E^* = σ 4 T_U³ ΔT = ε ΔT   ==>   ε = σ 4 T_U³

Für T_U = - 10°C = 263 K wird aus (98) mit (96):

(99) ε = 5,67 10^-8 W/m² K⁴ × 4 × 263³ K³ = 4,12 W/m² K

In [4] ist eine ähnliche Linearisierung vorgenommen worden. Ist die Oberfläche nicht schwarz (d.h. der Reflexionskoeffizient ist wellenlängenunabhängig = 0), sondern farbig (d.h. der Reflexionskoeffizient ist wellenlängenabhängig > 0) wird ε kleiner, kommt Konvektion und Wind dazu, wird ε größer. In [3, S. 143ff] ist b für verschiedene Stoffe angegeben, ausgewählt werden hier Kiesbeton (b = 1570 Ws^½/Km²) und ein Styropor-Schaumstoff (mittlerer Wert b = 49 Ws^½/Km²). Mit diesen Werten und (16) wird für t_N:

(100) Beton: 145212,79 s = 40,3 h Polystyrol: 141,45 s = 2,35 min

Beide Werte sind aus 2 Gründen nur Orientierungswerte: 1. Man hat es in der Praxis nicht mit ∞-dicken Wänden zu tun und 2. die Oberfläche besteht nicht nur aus einer ganz dünnen Oberflächenschicht, die für die Wärmeleitung unwesentlich ist, sondern hat eine gewisse Stärke. Wird der tägliche Wetterverlauf (mit typischen Zeiten um Stunden) betrachtet, so ist aus (100) trotzdem abzuschätzen, daß die Oberfläche von Betonwänden der fiktiven Umgebungstemperatur (Lufttemperatur plus Strahlungseinfluß, in [4] kritisiert Sonnentemperatur genannt) kaum folgt. Im Gegensatz dazu macht die Oberfläche einer Dämmstoffwand alle Temperaturbewegungen mit. Anders sieht es mit Witterungstrends aus (typischen Zeiten um Tage). Diesem Trend folgen etwa die Oberflächen beider Wände.

Obenstehende Lösung folgt weitgehend [3, S. 99ff]. α in [3] ist gleich dem hier verwendeten ε. Damit geht β in [3, Gl. (6.85)] über in:

(101)

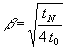
Wird die Oberfläche in [3] betrachtet, wird in [3, Gl. (6.85)]:

(102) ξ = 0 da x = 0 an der Oberfläche

Für den täglichen Temperaturgang (t₀ ≈ 24 h) folgt aus (101) und (100) wegen der großen bzw. kleinen Werte von β, daß mit [3, (6.90) und (6.91)] die Oberfläche von Beton diesem Temperaturgang kaum folgt und dazu noch mit fast 6 h Zeitverzögerung, die Oberfläche von Dämmstoff folgt dagegen fast sofort. Längeren Bewegungen (Tagen, d.h. >> 60 h) folgen beide Oberflächen. Wie (59) nahelegt, kann man jeden beliebigen Temperaturverlauf (Wärmestromverlauf) als geeignete Summe beliebig anderer Temperaturverläufe (Wärmestromverläufe) darstellen. Die Linearität von (59) gilt dann für jeden Verlauf unabhängig von den anderen.

Welche Auswirkungen hat das nun? Die zeitweisen hohen Temperaturen der Dämmstoffoberfläche werden im allgemeinen die Oberfläche nicht beschädigen, dagegen können die tiefen Temperaturen wegen Tauwasserausfall zu einer Oberflächenbelastung führen. Fließt das Wasser ab und verdunstet nicht wieder, wird die beim Tauen freiwerdende Wärme weitgehend der Wand zugeführt. Die Oberflächen beider Stoffe folgen dem langfristigeren Temperaturgang, der von den Eigenschaften der Oberfläche und nicht vom Wandmaterial dahinter abhängt. Das gilt zunächst erst einmal die ∞-dicke Wand, aber nach der Art der Herleitung (nur andere Gewichtsfunktion J (siehe (59)) ist anzunehmen, daß das auch für reale Wandstärken gilt. Das unterstreicht noch einmal die Aussagen in [1], daß der u-Wert bei allen Wandaufbauten gültig ist. Das der Einfluß der einzelnen Temperaturgänge unabhängig voneinander betrachtet werden kann, folgt aus der Linearität der Wärmeleitungsgleichung, wie in [1] gezeigt und auch in [3] angewandt wird.

Hinweisen möchte ich auch auf [8, S. 22 bis 37] wo ebenfalls die Wärmeleitungsgleichung mit Speicherung behandelt wird. Die in [8, S. 31] gemachte Bemerkung über die Vieldeutigkeit der Lösung bezieht sich auf ein mathematisch denkbares, aber real nicht realisierbares Phänomen (Wärmeexplosion). Außerdem könnte man das noch als kombinierte Anfangs- und Rand-Bedingungen sehen. Das bedeutet, daß in der Praxis die Lösung der Wärmeleitung mit Anfangs- und Rand-Bedingung eindeutig ist. Da die Anfangsbedingung bald abgeklungen ist folgt dann die Lösung eindeutig aus den Randbedingungen.

5. Literatur

[1] Ebel, J.: Wie steht es mit der Anwendbarkeit des U-Wertes?http://www.Ing-Buero-Ebel..de/Arbeiten/UWert/UWert.htm
[2] Stopp, F.: Operatorenrechnung. BSB B. G. Teubner Verlagsgesellschaft. Leipzig 1978
[3] Grigull, U.; Sandner, H.: Wärmeleitung. Springer-Verlag Berlin Heidelberg New York 1979
[4] Nehring, G.: Über den Wärmefluß durch Außenwände und Dächer in klimatisierte Räume infolge der periodischen Tagesgänge der bestimmenden meteorologischen Elemente. Gesundheits-Ingenieur 83 (1962) H. 7, S. 185 – 189; H. 8, S. 230 – 242; H. 9, S. 253 - 269
[5] Smirnow, W. L.: Lehrgang der höheren Mathematik Teil IV. VEB Deutscher Verlag der Wissenschaften. Berlin 1961
[6] Bronstein, I. N.; Semendjajew, K. A.: Taschenbuch der Mathematik. BSB B.G. Teubner Verlagsgesellschaft, Leipzig 1979
[7] Oberhettinger, F.; Badii, L.: Tables of Laplace Transforms. Springer-Verlag. Berlin Heidelberg New York 1973
[8] Doetsch, G.: Handbuch der Laplacetransformation Bd. III. Birkhäuser Verlag Basel und Stuttgart 1973
[9] Stefan 1879 - genaueres evtl. in [10]
[10] Boltzmann, L.: Ann. Phys. 22(1884) 31, 291 und 616
[11] Wien, W.: Ann. Phys. 58(1896) 662
[12] Jaworski, B.M. und Detlaf, A.A.: Physik griffbereit. Akademie-Verlag * Berlin 1973
[13] DIN EN ISO 9288: Wärmeschutz - Wärmeübertragung durch Strahlung - Physikalische Größen und Definitionen (ISO 9288:1989); Deutsche Fassung EN ISO 9288:1996. Ausgabe: 1996-08