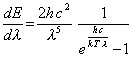
bzw.
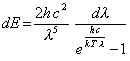
Treibhauseffekt und Physik
Die Einführung der EnEV wird auch mit der Notwendigkeit der Reduzierung der Treibhausgase begründet. Die Verringerung des Heizwärmeverbrauchs wird oft durch zusätzliche Dämmschichten erreicht. Nun gibt es Architekten, die ihre Ablehnung der EnEV u.a. mit dem Bestreiten des Treibhauseffektes begründen.
Es gibt Veröffentlichungen (z.B. [1]), in denen der Treibhauseffekts mit einem angeblichen Verstoß auf die Gesetze der Physik bestritten wird. Solche Artikel sind eine Mischung von Wissen und falschen Schlussfolgerungen.
Als Vorbemerkung eine Zusammenstellung der Abkürzungen:
Wenn man in der Dunkelheit mit dem Auto bei Nebel fährt, kann man gewisse Analogien zum Treibhauseffekt ziehen. Man kann nicht durch den Nebel sehen. Der Nebel verschluckt das Scheinwerferlicht. Aber der Nebel fängt praktisch an zu "leuchten", so dass der Autofahrer auch etwas von seinem Scheinwerferlicht abbekommt. Auch ist bekannt, dass z.B. rotes Licht den Nebel besser durchdringt als blaues (auch ein Grund für die rote Warnfarbe).
Ein angeblich wesentliches Argument gegen den Treibhauseffekt ist der 2. Hauptsatz der Thermodynamik. Dieser Satz besagt, dass Wärme nur von einem warmen zu einem kalten Körper strömen kann. Dazu wird beispielsweise Max Planck zitiert: "Wenn sich zwei unterschiedlich temperierte 'schwarze Körper‘ in einem luftleeren Raum gegenüberstehen, wird der kältere einen Nettoenergiegewinn erfahren und sich erwärmen, während sich der wärmere unter Bruttoenergieverlust abkühlt."
Der schwarze Körper muss noch erklärt werden. Landläufig versteht man unter einer schwarzen Oberfläche, dass auffallendes Licht fast nicht reflektiert, sondern verschluckt wird. In physikalischer Hinsicht versteht man darunter genau dasselbe - bloß ganz extrem, d.h. es wird alles Licht verschluckt. Aber nicht nur alles sichtbare Licht (d.h. Strahlung mit Wellenlängen von 0,4 μm bis 0,8 μm), sondern Strahlung mit beliebigen Wellenlängen. Aus dem 2. Hauptsatz folgt auch noch eine Eigenschaft, die man kaum vermutet - der erwähnte schwarze Körper strahlt bei bestimmter Temperatur von allen Körpern am stärksten. Man denke z.B. an die erwärmte schwarze Herdplatte. Der 2. Hauptsatz verlangt, dass vom wärmeren zum kälteren Körper ein Nettowärmestrom fließt. Das schließt ein, dass bei Temperaturgleichheit der Nettowärmestrom = 0 sein muss. Denn bei einen Nettowärmestrom ≠ 0 kühlt oder erwärmt sich ein Körper, wenn nicht noch andere Prozesse eine Rolle spielen. Eine kleine Abweichung von der Temperaturgleichheit würde ja einen Nettowärmestrom hervorrufen, der genau so gerichtet ist, dass diese Ungleichheit wieder aufgehoben wird. Da nun ein schwarzer Körper alle auftreffende Strahlung verschluckt, muss er im Temperaturgleichwicht genauso viel Energie abstrahlen, wie er verschluckt, sonst wäre ja der Nettowärmestrom nicht 0 - und das widerspräche dem 2. Hauptsatz.
Im weiteren wird davon ausgegangen, das eine Art "Nebel" zwischen Erdoberfläche (15°C) und Weltraum liegt. Der Weltraum hat gar keine Temperatur - die kosmische Hintergrundstrahlung entspricht einer Temperatur von ca. 3 K. Der "Nebel" soll eine Temperatur von ca. -47°C haben. Gibt es dann Widersprüche?
Wer die Formulierung von Max Planck als Gegenargument zitiert, hat die Formulierung nicht verstanden. Nettoenergiegewinn bedeutet, dass der wärmere Körper viel Wärme an den kälteren strahlt. Versteht man den Satz so, das der kältere Körper keine Wärme an den wärmeren Körper strahlt, dann versteht man den Satz falsch. Nettoenergiegewinn heißt, dass das Geschehen so passiert, dass vom wärmeren Körper mehr Wärme zum kalten als vom kalten zum warmen kommt. Dafür, dass das so ist, gibt es eine ganz einfache Erklärung. Im Moment der Wärmeabstrahlung "weiß" ja kein Körper, wo die ausgesandte Strahlung mal auftreffen wird. Die Strahlung kann in der Tiefe des Weltalls verschwinden, auf einen wärmeren Körper treffen oder auch auf einen kälteren. Das bedeutet die Ausstrahlung jedes Körpers geschieht unabhängig von der Umgebung. Aber ein schwarzer wärmerer Körper strahlt eben viel stärker, als ein schwarzer kühlerer Körper – und damit ist die Erfüllung des 2. Hauptsatzes gesichert. Noch ein Schmankerl, wenn eine oder beide Körper nicht schwarz sind. Dann kann der kühlere Körper ggf. mehr Energie abstrahlen als der wärmere, aber da ja jetzt die Körper die auftreffende Energie teilweise reflektieren, bleibt als Bilanz aller Vorgänge wieder übrig, das der kältere Körper mehr Wärme als der wärmere absorbiert. Abkühlen und Erwärmen geschehen aber nur, wenn nicht weitere Prozesse existieren, durch die z.B. die Körper ihre Temperatur behalten.
Widerspricht die Strahlung von diesem "Nebel" dem 2. Hauptsatz der Thermodynamik, dass Nettowärme nur vom warmen zum kalten Körper strömt? Nein, denn von den 390 W/m², die ein 15°C warmer Körper abstrahlt, bleiben zwar nur 300 W/m² in dem "Nebel" und 90 W/m² gehen im wesentlichen durch das "atmosphärischen Fenster (entspricht etwa der besseren Durchsichtigkeit von roten Licht beim normalen wenig dichten Nebel.)" von 8 μm bis 12 μm. Aber nur 150 W/m² werden zur Erde rückgestrahlt. Damit bleibt ein Nettowärmestrom von 150 W/m² (= 300W/m² - 150 W/m²) von der warmen Erde zum kalten "Nebel" übrig, d.h. der 2. Hauptsatz ist erfüllt. Der "Nebel" "weiß" natürlich nicht, das er zur Erde strahlt. Er strahlt selbstverständlich nach allen Richtungen. Aber da der "Nebel" als eine Art Schale um die ganze Erdkugel ist, bleibt die Strahlung zur Seite im "Nebel". Deshalb kann der "Nebel" nur nach oben und unten strahlen. Wenn er nach unten 150 W/m² strahlt, muss er nach oben (Richtung Weltraum) natürlich auch 150 W/m² abstrahlen. Das widerspricht auch wieder nicht dem 2. Hauptsatz, da der "Nebel" aus dem Weltall kaum Strahlung absorbiert. Mit den genannten 150 W/m² aus dem "Nebel" in den Weltraum und den 90 W/m², die durch die atmosphärischen Fenster direkt in den Weltraum strahlen, strahlt die Erde 240 W/m² (=150 W/m² + 90 W/m²) in den Weltraum ab. Da sich der "Nebel" weder erwärmt noch abkühlt, muss die Gesamtenergiebilanz ausgeglichen sein. Da 300 W/m² (= 150 W/m² nach unten + 150 W/m² nach oben) abgestrahlt werden, müssen auch 300 W/m² zugestrahlt werden. Aber genau dieser Wert war im 2. Satz dieses Absatzes als Zustrahlung von der Erde genannt. Theoretisch wird der "Nebel" auch noch von der Sonne erwärmt, aber in dem Wellenlängenbereich (entspricht im Bereich des sichtbaren Lichts z.B. einer farbigen Glasscheibe), in dem der "Nebel" absorbiert, liegt nur ganz wenig Sonnenstrahlung.
Auch eine weiteres Argument um den Treibhauseffekts (z.B. in [3]) zu bestreiten widerspricht dem 2. Hauptsatz. Teilweise strahlen Moleküle, die Strahlung absorbiert haben, die aufgenommene Energie selbst ab. Teilweise geschieht die Energieweitergabe bei Stoßprozessen usw.. Am Ende vieler Prozesse im "Nebel", muss der "Nebel" die aufgenommene Energie wieder abgeben, sonst würde sich der "Nebel" ja erwärmen. Aber die Aufklärung der Vorgänge im "Nebel" ist unabhängig davon, wie sich der "Nebel" als Ganzes verhält. Zu diesen uninteressanten Teilprozessen gehören auch gasdynamische Prozesse. Da die Erde 390 W/m² abstrahlt und im Weltraum nur 240 W/m² ankommen, müssen 150 W/m2 auf dem einen und/oder anderem Weg wieder zur Erdoberfläche zurückkehren. Auch die Vorgänge des Energietransports im "Nebel" sind in erster Näherung uninteressant, wichtig ist nur, dass der "Nebel" insgesamt überall auf der Erde die gleiche Temperatur hat. Einer der in erster Näherung uninteressanten Vorgänge ist z.B. die schon erwähnte seitliche Strahlung.
Das war mein Stand 2002. Heute weiß ich, daß die Abstrahlung nach oben und unten nicht gleich sein müssen. Gleichheit ist nur zufällig. Bei Gelegenheit kommt eine genauere Ausführung.
Nach dem Stefan-Boltzmannschen Gesetz hängt die Strahlung von der 4. Potenz der absoluten Temperatur ab. Wenn bei 15°C (= 288 K) die Strahlung 390 W/m² ist, dann ist also bei -47°C (= 226 K) die Strahlung gleich 390 W/m² • (226 K/ 288 K)4 = 148 W/m². Das sind bis auf die Rundungsfehler genau die gesuchten 150 W/m². Zweckmäßig wird an dieser Stelle auch die Strahlung einer -18°C (= 253 K) kalten Erde ohne Atmosphäre betrachtet: 390 W/m² • (253 K/ 288 K)4 = 232 W/m². Bis auf die Ungenauigkeiten sind das auch wieder die 240 W/m².
Weiterhin muss noch die Energiebilanz der Erde überprüft werden. Die Erde strahlt entsprechend dem vorher Geschriebenen von jedem m² der Erdoberfläche 240 W Tag und Nacht in den Weltraum ab. Wegen der Größe der Erdoberfläche (4πR²) sind das 4πR² • 240 W/m². Kleine Unterschiede in der Abstrahlung bestehen natürlich zwischen Tag und Nacht - aber die genaue Berücksichtigung zeigt, das im Mittel diese Unterschiede praktisch herausfallen. Jeden Tag (= 24 h) wird dementsprechend eine Gesamtenergie von 4π R² • 240 W/m² • 24 h abgestrahlt. Gleichzeitig wirft die Erde einen Schatten, d.h. hinter der Erde (von der Sonne aus gesehen) ist kein Sonnenlicht mehr. Dass das ein kreisförmiger Schatten ist, sieht man z.B. bei Mondfinsternissen. Wo ist nun die Sonnenstrahlung geblieben, die im Schatten fehlt? Natürlich auf der Erde, aber nur auf der beschienen Seite. Der größte Teil der Solarstrahlung liegt wieder in einem atmosphärischen Fenster (0,4 μm bis 1 μm) und erreicht deshalb die Erdoberfläche. Das im Schatten die Sonnenstrahlen nicht mehr da sind, merkt man selber im Sommer, wenn man sich in den Schatten stellt, weil einem zu warm ist. Also wird aus den Sonnenstrahlen genau der Teil herausgeschnitten, der durch den Querschnitt (πR²) der Erde gefallen wäre. In 24 h sind das insgesamt πR² • 24 h • S. Wenn sich die Erde weder erwärmt noch abkühlt, müssen die abgestrahlte und die zugestrahlte Energie gleich sein - also: 4πR² • 240 W/m² • 24 h = πR² • 24 h • S. Daraus folgt für S: 960 W/m² (= 4 • 240 W/m²). Das ist etwas weniger als die wirkliche Solarkonstante. Der Unterschied erklärt sich dadurch, das z.B. an Wolken und der Erdoberfläche ein Teil des Sonnenlichts reflektiert wird.
Bleibt als letztes noch zu überprüfen, ob durch die Durchlässigkeitsfenster der Erdatmosphäre tatsächlich nur 90 W/m² fallen. Dazu ist das Planksche Strahlungsgesetz auszuwerten:
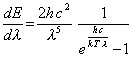
|
bzw. |
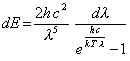
|
Da eine Integration nicht für jeden das Richtige ist, eine Excel-Auswertung, die jeder Excel-Nutzer machen kann. In Abhängigkeit von λ (in Spalte A) wird der Energieanteil dE in einem 0,1 μ m breiten Wellenlängenbereich (d.h. dλ = 0,1 μm) berechnet.
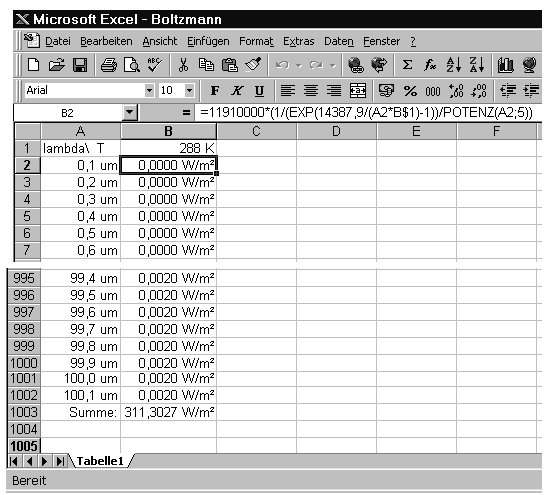
Bild 1: Screenshoot der Excel-Tabelle
Die angepasste Zahlenformel in jeder Excel-Zelle lautet
=11910000*(1/(EXP(14387,9/(A2*B$1)-1))/POTENZ(A2;5))
In der Zelle B$1 steht die Temperatur in Kelvin (also hier 288 K). In der Spalte A stehen die Wellenlängen. In der Spalte B (Strahlung) wird bei 10 μm (Zeile 101) der Maximalwert von 2,19 W/m² erreicht. Addiert man den gesamten Wellenlängenbereich von 0,1 μm bis 100 μm, so erhält man den Wert 311,3 W/m². Angesichts der einfachen Berechnung ein genügend guter Wert für die 390 W/m². Addiert man von 8 μm bis 12 μm (die Zeilen 81 bis 121) - also das Fenster, wo der "Nebel" nicht wirkt, so ergeben sich 86 W/m² - also wieder ausreichend genau die 90 W/m².
Bis jetzt war noch nichts über die Art des "Nebels" gesagt worden. Es sind dies die Treibhausgase CO2, Wasserdampf usw.. Über den Höhenbereich, in dem sich der Nebel befindet, ist damit nichts gesagt. Wenn man so will, reicht er z.B. als Ozon (ist wenig energierelevant) vom Erdboden und so hoch, wie die Atmosphäre reicht. Mit dem Satelliten ist man außerhalb der Atmosphäre und kann dort messen. Es wird genau das gemessen, was zu erwarten ist. Das zeigt z.B. Bild 2:
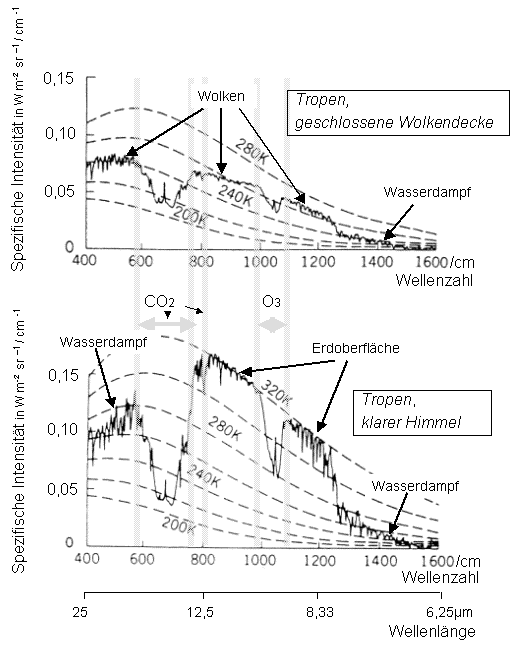
Bild 2: Emissionsspektrum der Erde (aus [4])
In Bild 2 ist die Wellenlängeabhängigkeit nicht in μm sondern in Wellenlängen/cm angegeben, also cm/λ.
Z.B.: 1cm/400 = 25 μm; 1cm/500 = 20 μm; 1cm/800 = 12,5 μm; 1cm/1000 = 10 μm; 1cm/1250 = 8 μm usw..
Eingetragen in die Messkurven sind die Strahlungskurven schwarzer Körper mit einer bestimmten Temperatur und die Stoffe, die jeweils den Hauptbestandteil des "Nebels" bilden.
Anmerkung: Bild 2 stammte zuerst aus [3] und hatte bei der Beschriftung einen übersehenen Fehler: statt richtig mW * m-2 * sr-1 * cm stand dort falsch mW * m2 * sr1 * cm. Das Diagramm stammt von Hanel [5] und das gleiche Bild aus einer früheren Veröffentlichung von Hanel ist auch in [6] verwandt.
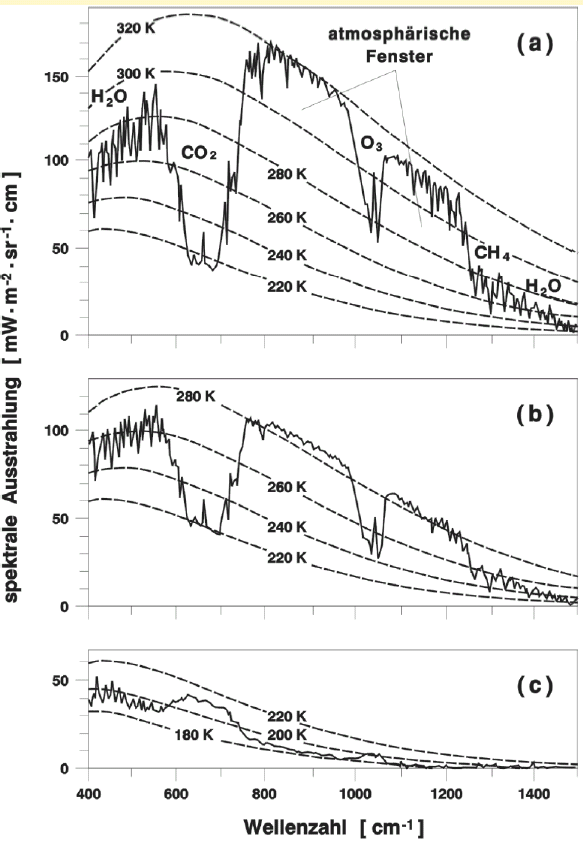
Bild 3: Emissionsspektrum in verschiedenen Breiten (aus [6]) Erklärungen nachfolgend.
Betrachtet man die Kurven in Bereichen des "Nebels", so zeigt sich am Äquator (Bild 3a: Sahara), in mittlerer Breite (Bild 3b: Mittelmeer) oder am Pol (Bild 3c: Antarktis) immer eine Strahlungstemperatur von ca. 220 K (= -53°C) herrscht, dagegen ist im Bereich der Fenster die Temperatur am Äquator 320 K (= 47°C), in mittleren Breiten 285 K (= 12°C) und am Pol 190 K (= -83°C). Es gibt also keine Unstimmigkeiten mit der Annahme, besonders wenn berücksichtigt wird, dass die Strahlung nicht von einem Schwarzkörper, sondern von der realen Oberfläche kommt. Allerdings sind in den dargestellten Wellenzahlbereichen die Abweichungen vom Schwarzkörper sehr gering. Für die Sahara heißt das, das zwar ein Teil reflektiertes Sonnenlicht mit gemessen wird, allerdings ist die Intensität in den betrachteten Wellenlängenbereichen gering (Temperaturwert nur gering zu hoch). Für die Antarktis bedeutet das, das die Schneefläche weniger als der Schwarzkörper strahlt (Temperaturwert gering zu niedrig). Zu erwartende Messwerte und alle physikalischen Gesetze sind also erfüllt. Unsicherheiten bestehen nur im Bereich der sehr vereinfachten Rechnungen. Von einem Hohlraum musste nie gesprochen werden.
Wie sich die Verhältnisse verändern, wenn der Nebel dichter wird, weiß jeder Autofahrer. Sorgen wir also dafür, dass der "Nebel" nicht dichter wird (z.B. Anreicherung der Atmosphäre mit CO2).
Dipl.-Physiker Jochen Ebel
Literatur:
[1] Thüne, W.: http://www.dimagb.de/info/thtreib3.htm (Kurzfassung von [2])
[2] Thüne, W.: Der Treibhausschwindel. Discovery Press. ISBN 3-9803768-6-9
[3] http://mitglied.lycos.de/climate/strahlung.htm funktioniert nicht mehr
[4] http://freenet-homepage.de/klima/wspeicher.htm
[5]Hanel, R. A. et al., Exploration of the solar system by infrared remote sensing, Cambridge University Press, 2003
[6]Volz, H.: Naturwissenschaftliche Anmerkungen zu Argumenten der Treibhausgasdiskussion. Erdöl, Erdgas, Kohle 116(2000), H.9 S. 431 - 436
| Impressum, Disclaimer | Zurück zur Startseite | letzte Änderung: 18.09.2009 |