Die Temperaturen auf der Erde, im Gewächshaus, im Auto usw. werden immer mit dem Begriff Treibhaus verbunden. Handelt es sich dabei immer um die gleiche Wirkung - oder wo sind Unterschiede? Um das festzustellen, muß man die Wirkung verstehen. Und von den Aufgezählten kennen alle am Besten das Auto.
Das Innere eines Autos ist ein Hohlraum - wie gut oder wie schlecht hängt von der Betrachtung ab. Für Schall ist es ein fast vollkommener Hohlraum, allerdings gut gedämpft, aber mit schlechter Isolierung gegen Außenschall. Für sichtbares Licht ist es so gut wie kein Hohlraum, denn die großen Fenster sind so große Öffnungen im Hohlraum, daß man kaum noch von Hohlraum sprechen kann. Für infrarotes Licht (Wärmestrahlung) sind die Glasscheiben praktisch undurchsichtig, so daß wieder ein sehr guter Hohlraum vorliegt.
Um die Temperaturen zu messen, ist ein Meßgerät notwendig, z.B. ein Temperaturfühler. Temperaturfühler haben oft eine Scheibenform. Mit dieser Form sind auch die Betrachtungen relativ einfach. Mit Scheibe ist im weiteren meist eine kleine dünne Scheibe gemeint, die auch ein Temperaturfühler sein kann, nur selten die Autoscheibe (Glasscheibe).
Ein einfaches Modell
Die Form des Autohohlraums ist sehr kompliziert. Für Betrachtungen der Verhältnisse im Hohlraum wird deshalb ein einfacheres Modell verwendet - eine Hohlkugel (Bild 1).

Bild 1: eine Hohlkugel
Die Wand der Hohlkugel soll warm sein - beispielsweise 39°C (= 312 K). Da jeder warme Körper eine Wärmestrahlung aussendet, ist das Innere der Hohlkugel von einer Wärmestrahlung erfüllt (Bild 2).
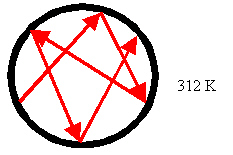
Bild 2: Hohlkugel mit Wärmestrahlung
Über die Stärke und Wellenlängenverteilung dieser Wärmestrahlung im Hohlraum macht die Plancksche Gleichung Aussagen. Diese Werte im Innern des Hohlraums anzugeben ist für die weitere Betrachtung nicht notwendig.
Trotzdem eine kleine Abschweifung: Bei Temperaturen unter 100°C ist von einer Wärmestrahlung fast nichts zu sehen (nur zu fühlen). Bei ca. 500°C ist eine Wärmestrahlung als schwache Rotglut zu sehen und verschiebt sich mit steigender Temperatur über gelb immer mehr in Richtung blau, was zu dem Eindruck weiß führt. Denken Sie bitte mal an die Farben Ihrer Kochplatte und einer Glühlampe mit Dimmer.
Im Hohlraum wird ein ausgesandter Wärmestrahl irgendwo wieder auf die innere Hohlraumwand treffen und dort teils verschluckt, teils reflektiert werden. Nach vielen Reflexionen ist von dem ursprünglich ausgesandten Strahl nicht mehr viel übrig, aber dafür sind wieder an anderen Stellen neue Strahlen entstanden, so daß immer das Hohlrauminnere mit der Strahlung angefüllt ist. Die weitere Untersuchung zeigt auch, daß Energiedichte und Wellenlängenverteilung dieser Strahlung (in der alle Strahlrichtungen gleichzeitig vorhanden sind) praktisch unabhängig von den Eigenschaften der Wandoberfläche sind und nur von der Temperatur der inneren Oberfläche abhängen.
Was passiert nun, wenn der Hohlraum eine kleine Öffnung erhält? Strahlung, die vor dem Bohren der Öffnung auf die Hohlraumwand getroffen wäre, findet dort keine Wand mehr vor und tritt ins Freie (Bild 3):
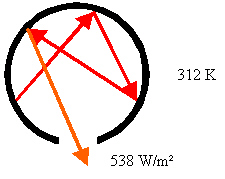
Bild 3: Hohlraum mit kleiner Öffnung
Für die Stärke dieser austretenden Hohlraumstrahlung (siehe [1, S.116/ Fußnote 20]) gilt das Stefan-Boltzmann'sche Gesetz:
Was passiert nun, wenn wir einen zweiten solchen Hohlraum nehmen und ihn mit dem ersten so zusammensetzen, daß Öffnung auf Öffnung liegt (Bild 4)?
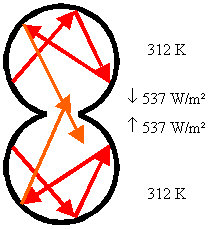
Bild 4: 2 Hohlräume mit gemeinsamer kleiner Öffnung
Eigentlich passiert gar nichts, denn die - aus dem oberen Hohlraum durch die Öffnung - austretende Strahlung "weiß" ja gar nicht, daß sie in den unteren Hohlraum einfällt, d.h. es bleibt bei den 537 W/m². Für den unteren Hohlraum gilt natürlich das entsprechende.
Was passiert nun, wenn in die kleine Öffnung eine noch kleinere Scheibe (grün) hereingebracht wird (Bild 5)?
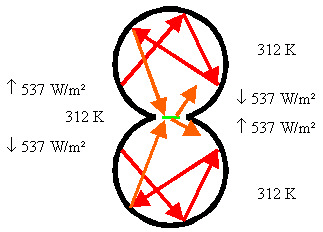
Bild 5: Hohlraum mit kleiner Scheibe
Eigentlich passiert auch wieder nichts. Ein Teil der Wärmestrahlung, die durch die Öffnung gehen wollte, trifft auf die Scheibe und wird dort verschluckt, wenn wir eine schwarze Oberfläche annehmen. Gleichzeitig wird die Scheibe aber selbst wieder Wärmestrahlung abstrahlen. Wenn die Scheibe weniger abstrahlen würde, als sie absorbiert, würde sie sich erwärmen bzw. umgekehrt. Ihre Temperatur wird sich also so einstellen, das sie genau so viel abstrahlt, wie sie absorbiert - und das ist im Beispiel bei 312 K der Fall. Die Scheibe verhält sich also praktisch für beide Hohlräume so, als wäre sie ein Stück der jeweiligen Hohlraumoberfläche.
Nun nehmen wir zunächst die Scheibe wieder heraus, bohren ein weiteres Loch (Durchmesser etwa gleich dem Durchmesser der kleinen Scheibe) und lassen durch dieses Loch einen Sonnenstrahl so fallen, das er die gemeinsame Öffnung passiert (Bild 6). Dabei soll der Sonnenstrahl eine Intensität von 780 W/m² haben. Dieser Wert wird mit Rücksicht auf die Schwächung der Intensität durch die Autoscheibe gewählt.
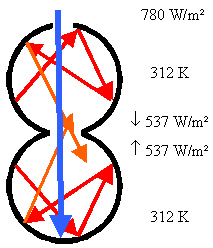
Bild 6: Sonnenstrahl in den Hohlraum
Was passiert nun? Im oberen Hohlraum gar nichts, denn der Sonnenstrahl trifft auf Grund der gewählten Strahlrichtung auf keine Oberfläche. Was passiert im unteren Hohlraum? Dort trifft der Sonnenstrahl auf die Hohlraumwand und könnte an der Auftreffstelle die Hohlraumwand erwärmen. Wenn die Wand schlecht wärmeleitend ist, passiert das auch (Ablage beim Auto z.b.). Wenn die Wand gut wärmeleitend ist (z.b. Metallteile) wird die Wärme zur äußeren Oberfläche weitergeleitet und zum Beispiel vom Wind weggeführt, also ändert sich die Temperatur der Wand fast nicht.
Nun kommt als letztes wieder unsere kleine Scheibe (gelb) in die gemeinsame Öffnung (Bild 7). Dabei ist die Richtung des Sonnenstrahls so gewählt, daß er genau auf die Scheibe trifft. Die Öffnung für den Sonnenstrahl war ja so gewählt, daß sie gleich den Scheibendurchmesser ist.
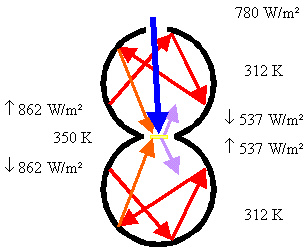
Bild 7: Sonnenstrahl mit kleiner Scheibe zwischen 2 Hohlräumen
Nun muß die kleine Scheibe wärmer werden als die Hohlraumwände, denn die Wärme kann im wesentlichen nur durch die Strahlung abgeführt werden. Vor dem Drauffallen des Sonnenstrahls hatte die Scheibe auch eine Temperatur von 312 K (Bild 5). Beim Drauffallen des Sonnenstrahls erwärmt sich die Scheibe (und zwar um so schneller, je weniger Masse sie hat, d.h. je dünner sie ist). Sie erwärmt sich so lange, bis sie genau so viel abstrahlt, wie sie absorbiert. Zum Absorbieren kommen 3 Anteile in Betracht; von oben 537 W/m², von unten 537 W/m² und der Sonnenstrahl mit 780 W/m² - insgesamt also 1854 W/m². Da die Scheibe eine einheitliche Temperatur annimmt, wird auf jeder Seite die Hälfte davon abgestrahlt - also 927 W/m². Jetzt hilft wieder das Stefan-Boltzmann'sche Gesetz. Nur wollen wir diesmal nicht wissen, wieviel abgestrahlt wird (das wissen wir nämlich schon), sondern bei welcher Temperatur das geschieht. Und da ergibt sich, daß die 927 W/m² bei 357 K (= 84°C) abgestrahlt werden.
Jetzt vergleichen wir die Temperatur mit einer bereits gemessenen [1] - und es ergibt sich eine sehr gute Übereinstimmung (gemessen 71°C).
Stimmt das Modell?
Bleibt zu fragen, inwieweit das Auto mit unserem Hohlraum zu vergleichen ist. Es wurde zwar die Scheibe in der Öffnung zwischen den beiden Hohlräumen platziert - ist das aber wesentlich? Nein, denn die Scheibe kann ohne Sonnenstrahl gar nicht "sehen", wo sie ist. In der Antarktis heißt dieses Phänomen "weiße Finsternis". Wenn der Himmel schneewolkenverhangen ist, alles schneebedeckt ist, sieht man nur weiß. Unmittelbar vor einem kann ein Berg oder eine Spalte sein - alles ist weiß, man sieht nichts. Erst mit einem zusätzlichen Lichtkegel sind Hügel und Spalten durch ihren Schattenwurf zu erkennen. Und hier leuchten alle Oberflächen mit 312 K - also eine Art weiße Finsternis. Deswegen ist die Form des Hohlraums beliebig - also auch das Autoinnere - die Einschnürung ist nicht notwendig. Ist aber das Loch für den Sonneneinfall klein? Ja, wenn auch im übertragenen Sinne. Die Wellenlängenverteilung der Wärmestrahlung (312 K) hat nur ganz kleine Anteile im Bereich des sichtbaren Lichts, von der Wärmestrahlung im Auto kann also von der Strahlung nur genausowenig entweichen, wie bei dem kleinen Loch im Modell. Daß das Sonnenlicht durch die großen Glasscheiben fällt, hat ein zusätzliches Aufheizen der Hohlraumoberfläche zur Folge. Aber je nach Wärmeabfuhr nach draußen (dort sind nur 29°C) wird die Hohlraumwand (Autokarosserie) nur mäßig auf die 39°C (312 K, Temperatur im Schatten im Autoinnern) aufgewärmt. Ohne diese Erwärmung wäre die Autokarosserie innen auch nur 29°C warm. Da die Autoscheiben durch die Sonne kaum aufgewärmt werden, ist die Hohlraumoberfläche nicht gleichmäßig 39°C warm, sondern stellenweise kühler. In der ersten Fassung dieser Abhandlung war von 29°C im Innenraum ausgegangen worden und damit ergaben sich etwa 7 K geringere Temperaturen. Die tatsächliche Hohlraumtemperatur dürfte zwischen diesen beiden Annahmen liegen. Damit fällt auf die kleine Scheibe (Temperaturfühler) etwas weniger als die 537 W/m², so daß die gemessene Temperatur auch kleiner sein muß. Und das ist auch so, denn es werden nur 71°C (allerdings mit Konvektion) statt der berechneten 84°C gemessen. Als vorletztes bleibt noch abzuschätzen, ob die 780 W/m² der Solarstrahlung real sind. Die Solarkonstante (Solarstrahlung auf die Erde) beträgt (gemessen und auch errechnet) 1368 W/m². Atmosphäre, Reflexion am Glas der Autoscheiben usw. lassen eine Abschwächung auf 57% realistisch erscheinen - und das ergibt 780 W/m².
Konvektion
Vorbemerkung: Strahlung geht von der Fläche aus, unabhängig von der Form. Bei der Konvektion spielt die Form des Körpers und die Umgebung eine gewisse Rolle. Wenn z.B. der Meßfühler eng an der Umgebung anliegt, entstehen andere Strömungsverhältnisse, als im freien Raum. Aber bei Abständen, die groß gegen die Abmessung des Meßfühlers sind, wird fast die freie Strömung erreicht. Wenn der Autor neue Kenntnisse zur Konvektion hat, wird die Rechnung fortgeschrieben. Das betrifft auch die Zahlenwerte aus der DIN, die ja nicht direkt eine Scheibe betreffen.
Alle Rechnungen bisher sind reine Strahlungsberechnungen. In [1] wird aber gerade eine verhinderte Konvektion für die Temperaturen verantwortlich gemacht. Wie groß ist wirklich dieser Anteil? Bei vielen Angaben zur Wärmeabführung sind Abstrahlung und konvektiver Wärmeverlust gemeinsam angegeben. Da die Abstrahlung aber schon angegeben ist, wird jetzt nur der konvektive Verlust gesucht und z.B. in [2, S. 8] gefunden. Bei der horizontalen Scheibe treten 2 Richtungen des Wärmeverlust auf nach oben (5,0 W/(m²K)) und abwärts (0,7 W/(m²K)).
Vor der weiteren Rechnung eine Zwischenbemerkung: wieso so große Unterschiede in Abhängigkeit von der Richtung des Wärmestroms (Faktor 7!!)? Ganz einfach: durch die warme Scheibe wird sowohl oberhalb als auch unterhalb die unmittelbar anliegende Luft erwärmt. Beide erwärmte Luftschichten sind leichter als die umgebende Luft und wollen deshalb aufsteigen (Heißluftballon). Die Luft oberhalb kann das und die nachströmende kühlere Luft nimmt erneut Wärme auf und führt sie ab. Die Luft unterhalb wird durch die Scheibe am Aufsteigen gehindert und dadurch ist die Strömung erheblich geringer. Es ist also zu sehen, daß alleine durch die Auftriebsverhältnisse eine Strömung entsteht, die die Wärmeabfuhr wesentlich bestimmt.
Welchen Einfluß hat nun die konvektive Wärmeabfuhr auf die Temperatur des Meßfühlers? Als Temperaturdifferenz werden 35 K angenommen (die weitere Rechnung zeigt, daß dieser Wert sinnvoll ist). Nach oben werden deshalb 175 W/m² (=5,0 W/(m²K)× 35 K) und nach unten 24 W/m² (=0,7 W/(m²K)× 35 K) abgeführt. Deshalb müssen nur noch 1655 W/m² (= 1854 W/m² - 175 W/m² - 24 W/m²) abgestrahlt werden. Das bedeutet, jede der 2 Seiten muß 828 W/m² abstrahlen. Und das verlangt eine Temperatur von 347 K (= 75°C). Da die gemessene Temperatur im Auto im Schatten 39°C ist, ist das etwa auch die Lufttemperatur. Und 75°C Temperatur der Scheibe und 39°C Lufttemperatur ergeben eine Temperaturdifferenz von 36 K - also die oben angesetzte Temperaturdifferenz. Die 1 K Unterschied entstehen aus Rundung - eine Rechnung mit mehr Stellen würde eine nicht vorhandene Genauigkeit vortäuschen. Die geringe Abweichung zwischen Meßwert (71°C) und Rechenwert (75°C) ist sehr gering und zeigt zugleich, daß die geschätzten Größen in [1] gut geschätzt sind. Aber die Meßwerte und Annnahmen in [1] führen eben zu dieser hervorragenden Übereinstimmung, obwohl offensichtlich damit etwas anderes bewiesen werden sollte. Zitat aus [1, S. 119]: "Jedem Klimatologen, der an den CO2-Treibhauseffekt glaubt, möchte ich diese Messung empfehlen, da ..."
Temperatur außerhalb des Autos
Als letztes bleibt die Frage in [1, S. 115] zu beantworten: "Man braucht nicht viel physikalischen Sachverstand, um sofort zu erklären, warum das Auto innen heiß ist: Es ist die Sonne, die das Auto innen so aufgeheizt hat. Etwas schwieriger ist aber schon die Frage zu beantworten, wieso es nicht auch außerhalb des Autos genauso heiß ist, obwohl dort die Sonne viel weniger behindert auf den Boden scheint." Die Frage muß anders herum gestellt werden: "Etwas schwieriger ist schon die Frage zu beantworten, wieso es innerhalb des Autos wärmer als auf dem Boden ist, weil der Sonnenschein dort behinderter ist". Das ist bereits erklärt. Dagegen ist die ursprüngliche Frage leicht zu beantworten. Der für eine Berechnung mit der Strahlungsbilanz erforderliche eingeschwungene Zustand (zumindest näherungsweise) liegt nicht vor und die Strahlung ist geringer.
Die Sonne scheint nicht lange genug, um die große Masse des Bodens zu erwärmen. Bei genügender Tiefe beträgt die Zeitkonstante Jahre. Deshalb ist die Bodentemperatur in dieser Tiefe ziemlich konstant und etwa gleich der Jahresmitteltemperatur. Das heißt, dort entspricht der Wert fast der Strahlungsbilanz. In unseren Breiten sind das ca. 9°C. Prinzipiell müßte noch der Wärmefluß aus dem Erdinnern berücksichtigt werden. Das sind nach [4] 0,0625 W/m2 (zitiert nach [5]). Bei einer angenommenen mittleren Temperatur von +15°C strahlt die Erde ca. 350 W/m² ab. Da wegen der Erdwärme mehr abgestrahlt werden muß, erhöht sich die Temperatur um 0,013 K. Und diese Temperaturänderung ist zu vernachlässigen - ob die mittlere Bodentemperatur nun +15°C oder -18°C ist. Die Bodentemperatur ist in [1] nicht gemessen. Eine Annahme von 20°C (=293 K) erscheint real. Als Schwarzkörper wäre dann die Strahlung 418 W/m². Die tatsächliche Strahlung ist geringer, weil der Boden kein Schwarzstrahler ist. Nach [3] liegt der Emissionsfaktor um 0,4, also ist die Abstrahlung um 167 W/m².
Wie erwähnt kommt von oben eine geringere Strahlung als im Auto. Obwohl die Solarstrahlung höher ist (vielleicht 900 W/m²), kommt von oben zusätzlich nur noch die von Treibhausgegnern geleugnete Gegenstrahlung (ein unmöglicher Begriff). Sie hat ca. 150 W/m² und stammt aus den erwärmten Bereichen der Atmosphäre, wobei der Begriff erwärmt relativ ist, denn es handelt sich um Temperaturen um -40°C. Insgesamt kommen damit von oben nur 1050 W/m² (= 900 W/m² + 150 W/m²), im Auto waren es dagegen 1252 W/m² (= 780 W/m² + 472 W/m²) auf den Temperaturfühler.
Da der Temperaturfühler eine kleine Masse hat (Zeitkonstante!), kann die Temperatur aus Strahlungsbilanz und Konvektion berechnet werden. Hier muß die Konvektion berücksichtigt werden, da in [1] richtig davon ausgegangen wird, das immer eine leichte Luftbewegung herrscht. Ist diese Luftbewegung unter 1 m/s, kann man sie praktisch nicht fühlen. Trotzdem ist der konvektive Wärmeverlust größer 12 W/(m²K) [2, Tabelle A.2]. Bei den 2 Seiten der Scheibe und angenommen 9 K Temperaturdifferenz (Fühlertemperatur 31°C, Lufttemperatur 22°C) sind das 216 W/m² (=12 W/(m²K)×2×9 K).
Damit ergibt sich als Bilanz 984 W/m² (1050 W/m² + 167 W/m² - 216 W/m²). Auf jeder der 2 Seiten wird die Hälfte abgestrahlt - also 492 W/m². Und dazu gehört eine Temperatur von 305 K (32°C). Gemessen wurden 31°C. Auch wieder eine hervorragende Übereinstimmung, obwohl einige Größen wieder nur geschätzt wurden.
Interessant ist auch noch die Temperatur bei Vernachlässigung der Konvektion. Von jeder Seite müssen dann nicht nur 492 W/m², sondern 600 W/m² abgestrahlt werden. Dazu gehört eine Temperatur von 320 K (48°C).
Vergleicht man die Temperaturen innen und außen in der Sonne mit (84°C/48°C) und ohne Konvektion (75°C/32°C) sieht man sofort, daß die Konvektion für die Treibhauswirkung nur eine untergeordnete Rolle spielt.
Irrtümer
Bei der Behandlung des Treibhauseffekts werden oft Vereinfachungen gemacht, die leicht dazu führen, daß man den Effekt mißverstehen kann (unbewußt und manchmal vielleicht auch bewußt).
Typische dieser Vereinfachungen sind, das die Strahlung "eingesperrt" ist. Strahlung kann man nicht "einsperren". Selbst bei sehr guten Spiegeln ist nach mehrmaliger Reflexion praktisch alle Strahlung absorbiert - und wegen der hohen Lichtgeschwindigkeit dauert das nur eine extrem kurze Zeit.
Zweiter Irrtum: Das Glas behindert den Wärmeaustritt durch seinen Wärmewiderstand. Das ist zwar nicht ganz falsch, wenn man an die sich einstellende Hohlraumtemperatur denkt, aber dabei wird die vom Glas ausgehende Wärmestrahlung vernachlässigt. Und die ist ganz wesentlich für die höhere Strahlung, die im Auto auf den Temperaturfühler oder z.B. auf den Boden im Frühbeet fällt. Die verringerte Konvektion im Frühbeet hat nur einen kleinen Anteil am Wärmeeffekt.
Grenzen
Wenn die Hohlraumwand wärmeisoliert ist, hat die Sonneneinstrahlung zur Folge, daß die Hohlraumwand noch stärker erwärmt wird (siehe Bild 6 und nachfolgender Text). Bei idealer Isolation (natürlich nur näherungsweise erfüllbar), kann die einfallende Solarenergie nur durch die Öffnung entweichen, durch die der Sonnenstrahl einfällt. D.h. es muß die austretende Strahlungsintensität gleich der einfallenden sein (780 W/m²). Dazu gehört eine Hohlraumtemperatur von 342 K (= 69°C). Dann muß die Scheibe sogar 1170 W/m² abstrahlen, d.h. sie würde sich auf 379 K (= 106°C) erwärmen. Wo ist die Grenze bei noch besser angepaßter Anordnung? Die ist durch den zweiten Hauptsatz gegeben: Es kann in einem abgeschlossenen System vom kühleren zum wärmeren Körper keinen Nettowärmestrom geben. Der Wärmestrom geht netto immer vom wärmsten zum kältesten Körper. Dabei sagt der zweite Hauptsatz überhaupt nichts über Bruttowärmeströme und Temperaturen in den Zwischenschritten aus.
Zwischenbemerkung für Menschen mit Physikkenntnissen. Der zweite Hauptsatz kann auch so formuliert werden, daß die Unordnung (Entropie) in einem abgeschlossenen (!!!) System nur zunehmen kann. Das bezieht sich nicht nur auf die Wärme direkt, sondern auch auf weiteres. Beispielsweise ist es einfach, in einem abgeschlossenen System im Wasser ein Häufchen Salz aufzulösen (Entropiezunahme - Wasser und Salz nicht mehr geordnet getrennt), aber das umgekehrte geht nicht. Man muß Wärme zuführen, um das Salz durch Verdampfen des Wassers zurückzuerhalten und muß damit das System erweitern. In einem großen System kann ein Teilsystem Entropie (Ordnung schaffen für Salz und Wasser) abgeben, dafür wird aber im Restsystem die Entropie erhöht. Ein Lebewesen in einer Umgebung ist ein hoch geordnetes System (geringe Entropie) und muß ständig Entropie an die Umgebung abgeben und dazu ist Energie notwendig. Geschieht das nicht mehr, stirbt das Lebewesen und die Unordnung (Entropie) nimmt zu (z.B. vermodern von Baumstämmen).
Und der wärmste Körper ist hier die Sonne mit 5780 K. Und an die kommt man weit heran. Denken Sie bitte mal an Ihre Kinderspielerein: mit einer Lupe wurde Papier in der Sonne zumindest verkohlt, wenn nicht sogar angebrannt. Und mit guten Spiegelanordnungen kommt man auf ein paar Tausend Grad. Man kommt sogar auf Temperaturen über die Solartemperatur: Mit solargepumpten Lasern [6] und [7] kann man über den Laserstrahl noch höhere Temperaturen erreichen. Aber der zweite Hauptsatz ist damit nicht verletzt, denn der Laser muß gekühlt werden - also netto strömt die Wärme von warm nach kalt. In den Begriffen von [1, S. 129] ist das eine Wärmepumpe, die Arbeit dafür stammt aus einer Maschine (natürlich keine Dampfmaschine). In der Praxis ist die Abgrenzung natürlich nicht so einfach wie in der Theorie durchzuführen.
Und der kälteste "Körper" ist der Weltraum mit ca. 3 K Strahlungstemperatur. Eine landläufige Temperatur hat der Weltraum nicht, da mit Temperatur landläufig immer die Temperatur eines Körpers gemeint ist.
Aber auch noch tiefere Temperaturen sind kein Verstoß gegen den zweiten Hauptsatz. Es muß nur wieder eine Wärmepumpe benutzt werden. Im Labor werden Bruchteile eines Kelvin erreicht - aber nur mit großem Aufwand.
Fazit:
Wenn schon der einfache Treibhauseffekt beim Auto nicht verstanden wird, hält es der Autor für unmöglich, den Angaben zum Treibhauseffekt in der Atmosphäre in [1] zu vertrauen. Schon beim Auto zeigt sich, daß die Autoscheiben den Temperaturfühler mit!!! (nicht alleine) erwärmen, obwohl sie kühler als dieser sind. Das ist kein Verstoß gegen den zweiten Hauptsatz der Wärmelehre, denn das System ist nicht abgeschlossen. Zu dem System gehört mindestens noch die Sonne. Für das Klimamodell ist also Bild 8 die richtige Darstellung:
Einige Bemerkungen zur Darstellung. Die gestrichelten Pfeile sind unwesentlich für die Strahlungsbilanz, sind aber prinzipiell vorhanden. Erinnert wird z.B. an die Ozonwirkung des UV-Anteils in der Solarstrahlung. Auch wenn Sonne und Weltraum weggelassen werden und die Pfeile im Nichts enden, bleibt das Modell richtig. Bedenklich wird die Darstellung aber, wenn die Wärmeströme vom Boden zur Stratosphäre und von der Stratosphäre zum Boden nicht zu einem Nettowärmestrom zusammengefaßt werden (der natürlich vom Boden zur Stratosphäre geht), sondern der Wärmestrom vom Boden zur Stratosphäre einfach weglassen wird (oder anderen das unterstellt wird) - und womit man dann scheinbar einen Verstoß gegen den zweiten Hauptsatz konstruieren kann. Nicht in der Darstellung sind auch die weiteren Energietransportmechanismen (z.B. Konvektion, Phasenumwandlung - z.B. Wasserdampf -Wasser, u.a.), die das Ganze noch modifizieren.
In dem Modell ist kein Verstoß gegen den zweiten Hauptsatz der Wärmelehre, denn der behandelt nur den Nettowärmestrom zwischen 2 unterschiedlich warmen Körpern in einem abgeschlossenen System. Das System Autoscheibe (Stratosphäre) - Temperaturfühler (Boden) ist nicht abgeschlossen denn ohne Einwirkung von außen - hier die sehr heiße Sonne - gibt es keinen Treibhauseffekt. Trotzdem würde eine Ausstrahlung von der Erde (die Erdoberfläche könnte ja von innen beheizt werden) durch die Stratosphäre behindert, denn jede Ausstrahlung vom Boden heizt die Stratosphäre auf - und die erwärmte Stratosphäre strahlt auch wieder auf den Boden. Und deshalb ist in [1, Seite 129] das Bild mit der Frage "funktioniert????:" zum atmosphärischen Treibhauseffekt unvollständig. Denn die Frage soll nach meiner Ansicht suggerieren, daß es nicht funktionieren könne. Aber dieser Eindruck kann nur entstehen, weil das Bild unvollständig ist. Vollständig ist Bild 8. Dabei gibt die Zahl der Pfeile die Strahlungsbilanz an. Jede Strahlungsbilanz gilt erst im eingeschwungenen Zustand. Deswegen ist die Strahlungsbilanz am Boden als Mittelwert zu verstehen.
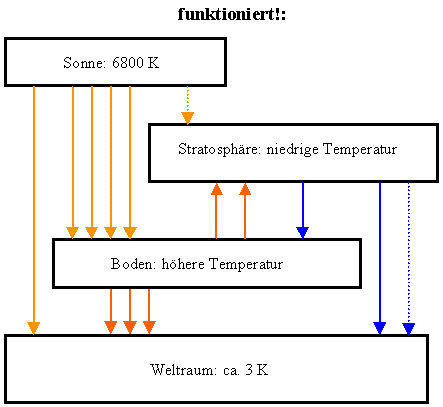
Bild 8: Wärmeströme beim atmosphärischen Treibhaus
Literatur
[1] Gerlich G.: "Die physikalischen Grundlagen der Treibhauseffekte und fiktiver Treibhauseffekte". In: Metzner H. (u.a.): "Treibhaus-Kontroverse und Ozon-Problem. Symposium der Europäischen Akademie für Umweltfragen, Leipzig, 9.-10. November 1995", Europäische Akademie für Umweltfragen e.V. (Hrsg.), Tübingen, 1996, S. 115-147.
[2] .....: DIN EN ISO 6946 : 1996
[3] .....: Emissionsfaktoren. http://www.omega.de. Herausgeber Newport Electronics GmbH
[4] http://metp02.mw.tu-dresden.de/Energiequellen/E_QUELLE/E-QUELL2.HTM
[5] Meinhold, R. : Energie aus der Tiefe der Erde. BSB. B.G. Teubner Verlagsgesellschaft Leipzig 1984
[6] http://hep.uchicago.edu/solar/laser.html
[7] Huff, Lloyd: Sun-pumped laser. IEEE-Journal of Quantum Electronics 1973 (Volume 9) Nr 6 ( June), S. 666 (ISSN0018-9197)
[8] ....: Änderungen durch Leserzuschriften. Wenn jemand seine Autorennennung wünscht oder zumindest keine Einwände hat, gibt das bitte in seiner Zuschrift ausdrücklich an. Auch der Wunsch nach Nichtnennung kann in der Zuschrift stehen.
| Impressum, Disclaimer | Zurück zur Startseite | letzte Änderung: 23.06.2004 |