 y(x) =
y(x) = 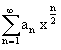
Rechnungsergänzungen zum "Lichtenfelser Experiment"
0. Inhalt
1. Entnormierung
2. Erwärmung des Gehäuses
3. Der Schornsteineffekt
4. Berücksichtigung der Wanddicke
5. Literatur
1. Entnormierung
Zur Auswertung der Messungen wird zum Vergleich die theoretische Kurve der Oberflächentemperatur nach Strahlungseinschaltung benötigt.
Diese Kurve ist normiert als Reihe in [2] Gleichung (68) dargestellt:
(1) y(x) =
y(x) = 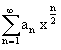
[2] Gleichung (68) zeigt a1 = ![]() , Gleichung (77) zeigt a2 = - 1, Gleichung (75) zeigt a3 =
, Gleichung (77) zeigt a2 = - 1, Gleichung (75) zeigt a3 = ![]() . Damit wird:
. Damit wird:
(2) y(x) =
y(x) = ![]()
![]() - x +
- x + ![]()
![]() - .....
- .....
Mit Gleichung (16) bis (17-3) ergibt sich (mit Ieo statt E, mit α statt ε):
(3) T(t) =
T(t) = ![]() y =
y = ![]() [
[![]()
![]() - x +
- x + ![]()
![]() - .....] =
- .....] = ![]() [
[![]()
![]() -
- ![]() +
+ ![]()
![]() - .....]
- .....]
 T(t) =
T(t) = ![]() [
[![]()
![]() -
- ![]() +
+ ![]()
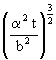 - .....] =
- .....] = ![]() [
[![]()
![]() -
- ![]() +
+ ![]()
![]() - .....]
- .....]
Oder:
(4) T(t) =
T(t) = ![]()
![]()
![]() -
- ![]() +
+ ![]()
![]() - .....
- .....
Jetzt wird eine Zeit to definiert:
(5)
![]() =
= ![]()
![]() ==>
==> ![]() =
= ![]()
Gleichung (3) wird durch ![]() geteilt und
geteilt und ![]() benutzt:
benutzt:
(6)
![]() =
= ![]() [
[![]() -
- ![]()
![]() +
+ ![]()
![]() t - .....] =
t - .....] = ![]()
![]() [1 -
[1 - ![]() +
+ ![]()
![]() t - .....]
t - .....]
 =
= ![]()
![]() [1 -
[1 - ![]() +
+ ![]()
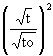 - .....]
- .....]
Damit können 2 wesentliche Größen bestimmt werden:
(7) Ieo =
Ieo = ![]()
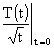 und α =
und α = ![]()
Gleichung (2) kann auch mit durch ![]() dividiert werden:
dividiert werden:
(8)
![]() =
= ![]() -
- ![]() +
+ ![]()
![]() - .....
- .....
Oder
(9)
![]()
![]() = 1 -
= 1 - ![]()
![]() +
+ ![]()
![]() - .....
- .....
Oder mit Einführung eines x* mit
(10) x* =
x* = ![]()
wird:
(11)
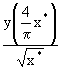
![]() = 1 -
= 1 - ![]() +
+ ![]()
![]() - .....
- .....
Oder mit ![]() = z:
= z:
(11)
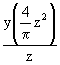
![]() = 1 - z +
= 1 - z + ![]() z2 - .....
z2 - .....
Nachfolgend ist diese Funktion dargestellt (einschließlich der Näherung der ersten 2 Glieder):
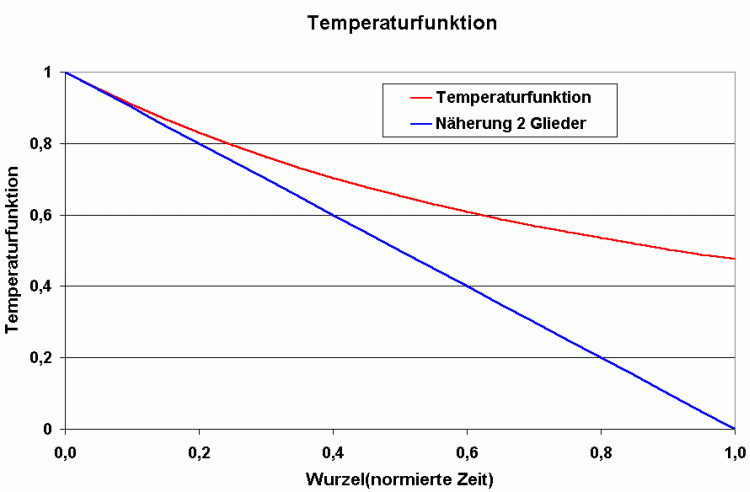
Wie man sieht, zeigen schon bei Zeiten ab 0,1 größere Abweichungen zwischen der Näherung und dem exaktem Wert, der die Auswertung erschwert.
Aber hier zeigt sich ein guter Ausweg, da in 4 äquidistanten Zeitabständen gemessen wurde, zwischen die auch die Trendgerade gelegt wird. Wird das auch bei der roten Kurve gemacht, ergeben sich - je nach gewähltem Zeitabstand - beispielsweise folgende Trendgeraden:
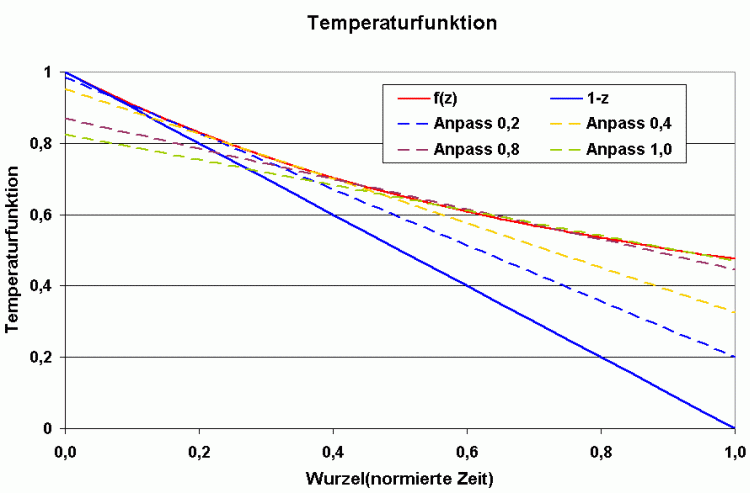
Wie man sieht, schneiden die Trendgeraden die Temperaturachse bei kleineren Werten als die Näherung und die Zeitachse bei größeren Werten. Damit man die Gleichungen (7) anwenden kann, sind die Daten der Trendgeraden entsprechend zu korrigieren. Die Werte zeigt das nachfolgende Diagramm:
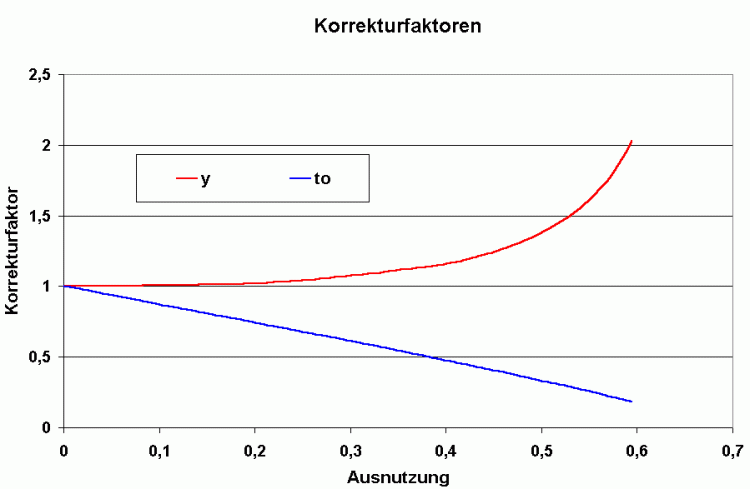
Mit diesen Faktoren (KE bzw. KZ) sind die Werte aus den Trendgeraden zu multiplizieren, um die Gleichungungen (7) anwenden zu können.
2. Erwärmung des Gehäuses
Da sich das Gehäuse erwärmt, erhöht sich wegen der steigenden Gehäuseabstrahlung auch die Leistung, die auf den Prüfling eingestrahlt wird.
Nimmt man als Näherung an, daß sich in den kurzen Zeiten des Lichtenfelser Experiments,
so ergeben sich folgende Gleichungen in der Laplaceform [2]:
Gewichtsfunktion des unendlichen Körpers [2, Gl. (12)]:
(12) EL − α TL = λ
EL − α TL = λ![]() TL
TL
Für das Gehäuse reicht das schon, wenn die Laplace-Transformierte der Einschaltfunktion berücksichtigt wird:
(13) EL =
EL = ![]()
Damit wird für die Laplace-Transformierte der Gehäusetemperatur:
(14)
![]() = (αG + λG
= (αG + λG![]() ) TLG
) TLG ==>
==> TLG =
TLG = ![]()
![]() mit τG =
mit τG = ![]()
Nun ist bei den hier betrachteteten Temperaturen die Einstrahlung etwa proportional der Übertemperatur. Damit ist die Laplace-Transformierte der Gehäuseeinstrahlung auf den Prüfling gleich der Gleichung (14). Die Abstrahlwerte, αG, Geometriefunktionen usw. werden zu einem Faktor κ zusammengefaßt. Damit wird die gesamte Einstrahlung auf den Prüfling:
(15)
![]() +
+ ![]() − αp TLp = λp
− αp TLp = λp![]() TLp
TLp
Durch Ausklammern entsteht:
(16) Eo (
Eo (![]() +
+ ![]() ) = (αp + λp
) = (αp + λp![]() ) TLp
) TLp
Durch Umstellen wird daraus:
(17) TLp =
TLp = ![]() (
(![]() +
+ ![]() )
)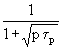
 mit
mit  τG =
τG = ![]()
Die Laplace-Transformierte (17) steht kaum in einem Tabellenbuch. Sie ist deshalb durch Partialbruchzerlegung in eine Summe aufzubereiten, deren Summanden in Transformationstabellen stehen. Dazu folgender Ansatz:
(18) (
(![]() +
+ ![]() )
)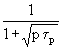 =
= ![]() +
+ ![]() +
+ ![]() +
+ 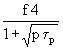
Die Lösung ist:
(19) f1 = 1 + κ
f1 = 1 + κ f2 = -κ
f2 = -κ![]() −
− ![]() (1 + κ
)
(1 + κ
) f3 =
f3 = 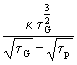
 f4 =
f4 = 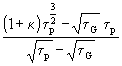
Für die einzelnen Summanden von (18) wird die Rücktransformation mit Tabellen gemacht. Nach Umsortierung wird daraus:
(20) Tp =
Tp = ![]() {
{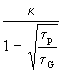 [1 -
[1 - 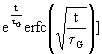 +
+ 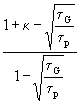 [1 -
[1 - 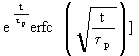 }
}
Der Ausdruck in den eckigen Klammern ist die Funktion y(x) (siehe Gl. (1)):
(21) Tp =
Tp =![]() {
{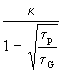 y(
y(![]() )+
)+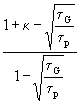 y(
y(![]() )}=
)}=![]() {y(
{y(![]() )+ κ
)+ κ
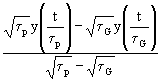 }
}
Mit Gleichung (2) werden wieder die ersten Glieder genommen:
(22) Tp = ![]() {(
{(![]()
![]() -
- ![]() +
+ ![]()
![]() - ....) +
- ....) + 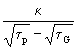 [
[![]() (
(![]()
![]() -
- ![]() +
+ ![]()
![]() - ....) -
- ....) - ![]() (
(![]()
![]() -
- ![]() +
+ ![]()
![]() - ....)] }
- ....)] }
![]() bzw.
bzw.![]() wird in die runden Klammern hineinmultipliziert und t-potenzgleiche Glieder zusammengefaßt (das Glied mit
wird in die runden Klammern hineinmultipliziert und t-potenzgleiche Glieder zusammengefaßt (das Glied mit ![]() ergibt dabei 0):
ergibt dabei 0):
(23) Tp =
Tp = ![]() {(
{(![]()
![]() -
- ![]() +
+ ![]()
![]() - ....) +
- ....) + 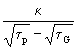 [
[![]() -
- ![]() +
+ ![]() (
(![]() −
−
![]() ) - ....] }
) - ....] }
Vorstehende Gleichung wird durch ![]() dividiert:
dividiert:
(24)
![]() =
= ![]() {(
{(![]()
![]() -
- ![]() +
+ ![]()
![]() - ....) +
- ....) + 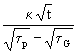 [
[![]() -
- ![]() +
+ ![]() (
(![]() −
− ![]() ) - ....] }
) - ....] }
Vorstehende Gleichung läßt sich weiter vereinfachen, indem die Differenzen in den eckigen Klammern auf den Hauptnenner gebracht werden und dann gekürzt wird:
(25)
![]() =
= ![]() {(
{(![]()
![]() -
- ![]() +
+ ![]()
![]() - ....) + κ
- ....) + κ
![]() [
[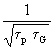 −
−
![]() (
(![]() +
+ ![]() ) - ....] }
) - ....] }
Zieht man das absolute Glied aus den geschweiften Klammern (und schreibt den vorderen Term analog Gl. (6)) und fast anders zusammen, wird:
(26)
![]() =
= ![]()
![]() {1 −
{1 − ![]()
![]() (1 − κ
(1 − κ![]() ) +
) + ![]() (1 - κ
(1 - κ 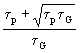 ) - .... }
) - .... }
3. Der Schornsteineffekt
Durch die Erwärmung des Gehäuses setzt ein Luftstrom ein, wodurch die Größe α in den Abschnitten 1. und 2. zeitabhängig wird.
Die Rechnung erfolgt unter den Annahmen des Abschnitts 2., zusätzlich kommt als weitere Annahme (die sicherlich gut erfüllt ist) dazu, daß die Luftgeschwindigkeit proportional der Gehäusetemperatur ist und unabhängig von der Prüflingsoberflächentemperatur.
Gesucht wird der zeitliche Verlauf der Oberflächentemperatur unter Berücksichtigung des Luftstrom, der von der Gehäusetemperatur angetrieben wird (Auftrieb).
Der Weg dieses Luftstroms: Die erwärmten Seitenwände des Gehäuses sorgen für den Auftrieb. Da das Gehäuse oben einen Deckel hat, strömt die erwärmte "leichte" Luft an der vorderen oberen Kante des Deckels ab. Die weggeströmte Luft wird ersetzt, indem unten nicht erwärmte Luft nachströmt. Dabei muß dies nicht erwärmte Luft über die Oberfläche des Prüflings strömen, da der Prüfling unten ist.
Für den Wärmeübergangswiderstand gilt (Angabe in [9, Formel 4.33]):
(27) α = Konstante1 + Konstante2 ×
α = Konstante1 + Konstante2 × ![]()
Die Werte der Konstanten 1 und 2 bringen hier zunächst nichts, da in die Kühlwirkung noch weitere Einflüsse eingehen.
Da mit der Annahme Luftgeschwindigkeit proportional Gehäusetemperatur TG gearbeitet wird, kann (27) auch so formuliert werden:
(28) α = Konstante1 + Konstante3 ×
α = Konstante1 + Konstante3 × ![]()
Der Teil, der Folge von Konstante1 ist, ist schon gelöst. Nun ist der Teil mit Konstante3 zu lösen.
Bei der Lösung der Dgl. hatte sich die Laplace-Transformation bewährt. Leider führt dieser Weg hier nicht direkt zum Ziel.
Wegen der Zeitabhängigkeit von TG ist die Laplace-Transformierte von Tp nicht mehr so einfach zu finden. Vorher war die Transformation einfach:
(29) Tp(t) <==> TpL(p)
Tp(t) <==> TpL(p)
Jetzt wird aber gesucht
(30)
![]() Tp(t) <==> ?
Tp(t) <==> ?
Selbst schon eine einfache e-Funktion macht das Ganze fast unlösbar:
(31) e- h t Tp(t) <==> TpL(p + h)
e- h t Tp(t) <==> TpL(p + h)
Unlösbar, weil die Bildfunktion noch nicht bekannt ist und deswegen unbekannt ist, wie die verschobene Bildfunktion im Verhältnis zur ursprünglichen Bildfunkion steht.
Deswegen wird ein etwas anderer Weg gewählt, die Störungsrechnung. Dabei wird davon ausgegangen, daß die Veränderung von α eine kleine Störung ist. Deswegen kann die Lösung als Summe von Einzellösungen berechnet werden, die die Störung immer besser berücksichtigen.
(32) Tp(t) =
Tp(t) = ![]()
α wird aufgeteilt:
(33) α = αp + αt(t)
α = αp + αt(t)
Aus (15) wird damit (L{}= Laplace-Transformierte):
(34)
![]() +
+ ![]() − L{(αp + αt(t))
− L{(αp + αt(t)) ![]() } = λp
} = λp![]() L{
L{![]() }
}
bzw.
(35)
![]() +
+ ![]() − αp
− αp ![]() −
L{αt(t)
−
L{αt(t) ![]() } = λp
} = λp![]()
![]()
Diese Gleichung ist auseinander zu nehmen, um jede Gleichung einzeln zu lösen:
(36)
![]() +
+ ![]() − αp TpLo = λp
− αp TpLo = λp![]() TpLo
TpLo
und:
(37) − αp TpLn − L{αt(t) Tp(n-1)} = λp
− αp TpLn − L{αt(t) Tp(n-1)} = λp![]() TpLn
TpLn für n = 1 bis ∞
für n = 1 bis ∞
Umgestellt wird daraus:
(38) L{αt(t) Tp(n-1)} = − (αp + λp
L{αt(t) Tp(n-1)} = − (αp + λp![]() ) TpLn
) TpLn für n = 1 bis ∞
für n = 1 bis ∞
Weiter umgestellt:
(39) TpLn = −
TpLn = − 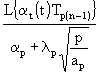
 für n = 1 bis ∞
für n = 1 bis ∞
Vorstehende Gleichung ist nun rückzutransformieren. Dabei ist auf der rechten Seite die Produktregel für Bildfunktionen anzuwenden. Der Zähler ist einfach rückzutransformieren:
(40)
![]() <==>
<==> ![]()
Auch die Rücktransformation des Nenners als Bruch ist mit Tabellen einfach:
(41)
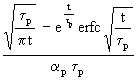 <==>
<==> 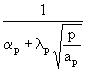
Mit der Produktregel, (40) und (41) ist nun (39) zu lösen (mit u als Zeitintegrationsvariable):
(42) Tpn = −
Tpn = − 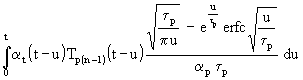
Mit der Substitution u/τp = x wird:
(43) Tpn = −
Tpn = − 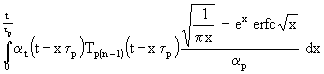
An vorstehender Gleichungen sind einige Umformungen zu machen. Aus (28) folgt:
(44) αt = Konstante3 ×
αt = Konstante3 × ![]()
Für TG gilt:
(45) TG = TG max y
TG = TG max y![]()
Faßt man Konstante3 × ![]() zu einem Stör-αs zusammen:
zu einem Stör-αs zusammen:
(46) αs = Konstante3 ×
αs = Konstante3 × ![]()
und definiert für jedes Glied der Reihe (32)
(47) Tpn(t) =
Tpn(t) = ![]()
so wird aus (43):
(48)
![]() = −
= −
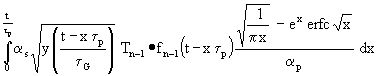
Zieht man die konstanten Glieder aus dem Integral heraus und definiert:
(49)
![]()
so kann Tn direkt angegeben werden und (48) vereinfacht sich:
(50)
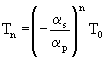
(51)
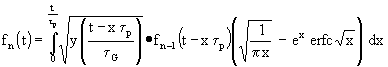
(52) Zur rechnerischen Vereinfachung wird (51) noch auf t = z × τp normiert, ein Faktor β = τp/τG und Funktionen hn(z) = fn(z × τp) eingeführt. Damit wird aus (51):
(53)
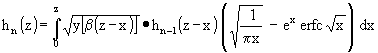 beginnen mit h0 = 1
beginnen mit h0 = 1
Zur Abschätzung der Größe von h werden in vorstehender Gleichung alle Funktionen maßvoll maximiert. Die runde Klammer mit ex wird maximiert, indem das Produkt mit ex einfach weggelassen wird:
(54)
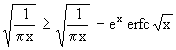
Der Term mit β wird folgendermaßen maximiert:
Für y(x) wird eine einfache Vergleichsfunktion gesucht, die immer größer als y(x) ist. Mit den noch zu bestimmenden Zahlen μ und φ soll das der Fall sein:
(55)
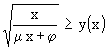
Das den Grenzen x = 0 und x −−> ∞ folgen Grenzen für φ und μ:
(56) φ < 1 bei x −−> ∞ und μ < π/4 = 0,7854
φ < 1 bei x −−> ∞ und μ < π/4 = 0,7854
Gewählt werden:
(57) φ = 0,93
φ = 0,93 und
und μ = 0,78
μ = 0,78
Die Kontrolle ergibt, daß diese Näherung maximal 34 % größer ist - und zwar bei x etwa 0,8.
Mit diesen Näherungen geht (53) über in:
(58)
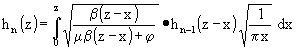 beginnen mit h0 = 1
beginnen mit h0 = 1
Speziell für h1:
(59)
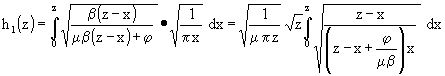
Um das Integral besser auswertbar zu machen, setze ich z - x = z y und μ/(zφβ) = f. Damit wird (Vertauschen der Integrationsgrenzen beachten):
(60)
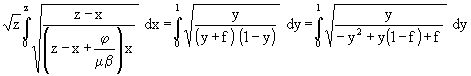
Eine Lösung des letzten Integrals ist mir nicht bekannt. Aber verschiedene Grenzfälle können betrachtet werden. Z.B. im Zähler y durch den Größtwert ersetzen (= 1). Dann ist das Integral als Nr. 241 in [14] tabelliert:
(61)
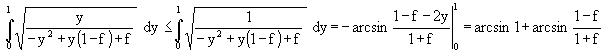
Für kleine Werte von f wird:
(62)
![]()
Für große Werte von f wird:
(63)
![]()
Für f = 0 und f −−> ∞ läßt sich (60) exakt lösen:
(64)
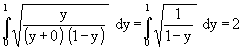
(65)
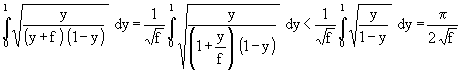
Für (64) ist der Wert von (62) mit 2/π = 0,63 und für (65) ist (63) mit π/4 = 0,78 zu multiplizieren. Da die Abhängigkeit von (61) von f monoton ist, wird das auch für den Korrekturwert, der von 0,63 auf 0,78 steigt. Wenn das so ist, dann ist (61) höchstens kleiner als die Korrektur mit dem größten Korrekturwert. Deswegen dürfte gelten:
(66)
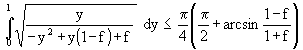
Für kleine z wird f groß und dann gilt mit (59) und (63):
(67)
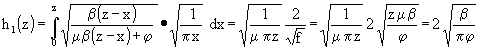
Für große z wird f klein und dann gilt mit (59) und (62):
(68)
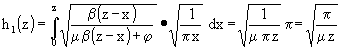
Aus (67) und (68) wird ein h1(z) zusammengesetzt, daß zumindest asymptotisch richtig ist
(67)
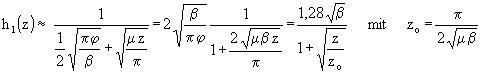
Aus (50), (52) und (67) folgt, daß die Reihe für
(68)
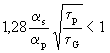
konvergiert. Da αs << αp als kleine Störung ist, und bei dem gewählten Versuchsaufbau τp < τG oder nur unwesentlich größer ist die Konvergenz immer gesichert.
Aus (67) folgt auch noch eine charakteristische Zeit:
(69)
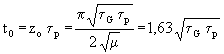
Durch Eo, αp (==> τp wenn bp vorausgesetzt wird), τG, "kappa" und αs existieren 5 unabhängige Konstanten. Da nur die 4 Meßwerte (bei 2,5 min, 5 min, 7,5 min und 10 min) vorhanden sind können diese sogar bei Vorhandensein von Meßfehlern fast immer erfüllt werden - ja ein Parameter ist sogar in bestimmten Maß frei wählbar.
4. Berücksichtigung der Wanddicke
In den bisherigen Betrachtungen wurde immer von einer ∞ Dicke der bestrahlten Flächen ausgegangen. Nun ist noch zu überprüfen, inwieweit das gilt.
Ausgangspunkt ist die eindimensionale WLG ohne innere Wärmequellen bei homogenen Material:
(70)
![]()
Vorstehende Gleichung wird nach x differenziert und mit λ multipliziert. Wegen
(71)
![]()
![]()
Geht dadurch (70) über in (formal die gleiche Gleichung, aber für q statt T):
(72)
![]()
Für eine ∞ dicke Schicht ist die Lösung bekannt [14, S.66]:
(73)
![]()
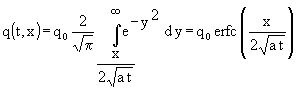
Die Fehlerfunktion ist tabelliert, z.B. in [13, S. 155, Tab. G.1.], allerdings nur erf selber.
Wie hilft diese Lösung weiter? Die WLG ist eine lineare Gleichung. Damit sind Summen von Lösungen wieder Lösungen der WLG.
Deswegen helfen hier Symmetriebetrachtungen weiter.
Bei einer Wandstärke w wird eine zweite Wärmequelle mit qo bzw. −qo am Ort 2w angenommen. Bei +qo ist der Wärmestrom = 0 am Ort w (ideale Dämmung), da die von der zweiten Wärmequelle der Wärmestrom den gleichen Betrag hat, aber entgegengesetzt ist. Bei −qo ist die Temperatur = 0 am Ort w (ideale Ableitung), da die von der zweiten Wärmequelle die Temperatur den gleichen Betrag hat, aber entgegengesetzt ist.
Dieser Wärmestrom ist die Störung des ursprünglichen Wärmestroms an der Oberfläche, d. h. bei x = 0.
Nun sind diese Erkenntnisse auf den vorliegenden Fall des Lichtenfelser Experiments anzuwenden. Der in das Material eindringende Wärmestrom ist nicht konstant, sondern nimmt wegen der Oberflächenverluste ab. Deswegen wird der Wärmestrom durch (73) nicht korrekt beschrieben, da für (73) ein konstanter Wärmestrom qo angenommen wurde. Wenn für den Wärmestrom ein Wärmestrom angenommen wird, der konstant gleich dem Maximalwert ist, so ist der tatsächliche Wärmestrom immer kleiner - und das trifft auch auf den störenden Wärmestrom der zweiten Wärmequelle zu.
Für die Wärmeströmung an der Oberfläche ist die zurückgelegte Strecke von der zweiten Wärmequelle 2w. Das Argument u für das Fehlerintegral ist:
(74)
![]()
![]()
Mit diesem Wert kann aus [13, Tab. G.1.] die maximale Störung abgelesen werden bei w = 4 cm und t = 10 min:
| Mineralwolle | Styropor | Holzfaserplatte | Fichte | Ziegel | |
a |
1,00E-06 mē/s |
1,33E-06 mē/s |
1,90E-07 mē/s |
1,85E-07 mē/s |
4,63E-07 mē/s |
u |
1,63 |
1,41 |
3,74 |
3,80 |
2,40 |
Störung |
2,09 % |
4,55 % |
0,00 % |
0,00 % |
0,07 % |
Die Störungen sind zwar auch bei MiWo und PS schon sehr gering, aber selbst diese geringen Werte sind aus folgenden Gründen viel zu hoch: Die berechneten Störungen sind unter der Annahme ideale Dämmung bzw. ideale Ableitung berechnet. Nun ist die Unterlage aber das gleiche (oder fast gleiche) Material wie der Prüfling. Damit ist die zweite Wärmequelle als viel schwächer anzusetzen, bzw. die Unterlage ist die Fortsetzung des Prüflings und dann ist für w nicht die Dicke des Prüflings (4 cm) sondern die Dicke von Prüfling + Unterlage (ca. 14 cm) anzusetzen.
Damit spielt bei allen Prüflingen die Endlichkeit der Unterlage keine Rolle.
5. Literatur
| [2] | Ebel, J.: | Oberfläche und Speicherung. http://www.Ing-Buero-Ebel.de/Arbeiten/Wand/OberflaecheL.htm |
| [9] | Mende, D. und Simon, G.: | Physik - Gleichungen und Tabellen. VEB Fachbuchverlag Leipzig 1971 |
| [13] | Grigull, U. • Sandner, H.: | Wärmeleitung. Springer-Verlag Berlin Heidelberg New York 1979 |
| [14] | Bronstein, I. N.; Semendjajew, K. A.: | Taschenbuch der Mathematik. BSB B. G. Teubner Verlagsgesellschaft, Leipzig 1979 |