Von
M. PLANCK
(Vorgetragen in der Sitzung vom 19. Oktober 1900)
Die von Hrn. KURLBAUM in der heutigen Sitzung mitgeteilten interessanten Resultate der von ihm in Gemeinschaft mit Hrn. RUBENS auf dem Gebiete der längsten Spektralwellen ausgeführten Energiemessungen haben die zuerst von den Herren LUMMER und PRINGSHEIM auf Grund ihrer Beobachtungen aufgestellte Behauptung nachdrücklich bestätigt, daß das WIENsche Energievcrteilungsgesetz nicht die allgemeine Bedeutung besitzt, welche ihm bisher von mancher Seite zugeschrieben worden war, sondern daß dieses Gesetz vielmehr höchstens den Charakter eines Grenzgesetzes hat, dessen überaus einfache Form nur einer Beschränkung auf kurze Wellenlängen bzw. tiefe Temperaturen ihren Ursprung verdankt1). Da ich selber die Ansicht von der Notwendigkeit des WIENschen Gesetzes auch an dieser Stelle vertreten habe, so sei es mir gestattet, hier kurz darzulegen, wie sich die von mir entwickelte elektromagnetische Theorie der Strahlung zu den Beobachtungstatsachen stellt.
Nach dieser Theorie ist das Energieverteilungsgesetz bestimmt, söbald die Entropie S eines auf Bestrahlung ansprechenden linearen Resonators als Funktion seiner Schwingungsenergie U bekannt ist. Ich habe indes schon in meiner letzten Arbeit über diesen Gegenstand hervorgehoben [1], daß der Satz der Entropievermehrung an und für sich noch nicht hinreicht, um diese Funktion vollständig anzugeben; zur Ansicht von der Allgemeinheit des WIENschen Gesetzes wurde ich vielmehr durch eine besondere Betrachtung geführt, nämlich durch die Berechnung einer unendlich kleinen Entropievermehrung eines in einem stationären Strahlungsfelde befindlichen Systems von n gleichen Resonatoren auf zwei verschiedene Weisen, wodurch sich die Gleichung2) ergab:
wobei
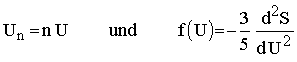
aus welcher dann das WIENsche Gesetz in der Form hervorgeht:
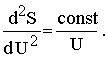
In jener Funktionalgleichung stellt der Ausdruck auf der rechten Seite sicher die genannte Entropieänderung dar, weil sich n ganz gleiche Vorgänge unabhängig voneinander abspielen, deren Entropieänderungen sich daher einfach addieren müssen. Dagegen würde ich es wohl für möglich, wenn auch immer noch für nicht leicht begreiflich und jedenfalls schwer beweisbar ansehen, daß der Ausdruck links nicht allgemein die ihm früher von mir zugeschriebene Bedeutung besitzt, mit anderen Worten: daß die Werte von Un, dUn und ΔUn gar nicht hinreichen, um die fragliche Entropieänderung zu bestimmen, sondern daß dazu auch U selber bekannt sein muß. Im Verfolg dieses Gedankens bin ich schließlich dahin gekommen, ganz willkürlich Ausdrücke für die Entropie zu konstruieren, welche, obwohl komplizierter als der Wiensche Ausdruck, doch allen Anforderungen der thermodynamischen und elektromagnetischen Theorie ebenso vollkommen Genüge zu leisten scheinen wie dieser.
Unter den so aufgestellten Ausdrücken ist mir nun einer besonders aufgefallen, der dem WIENschen an Einfachheit am nächsten kommt und der, da letzterer nicht hinreicht, um alle Beobachtungen darzustellen, wohl verdienen würde, daraufhin näher geprüft zu werden. Derselbe ergibt sich, wenn man setzt3):
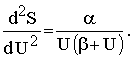
Er ist bei weitem der einfachste unter allen Ausdrücken, welche S als logarithmische Funktion von U liefern (was anzunehmen die Wahrscheinlichkeitsrechnung nahe legt) und welche außerdem für kleine Werte von U in den obigen WIENschen Ausdruck übergehen. Mit Benutzung der Beziehung
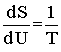
und des WIENschen ,,Verschiebtingsgesetzes"4) erhält man hieraus die zweikonstantige Strahlungsformel:
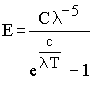
welche, soweit ich augenblicklich sehen kann, den Gang der seither publizierten Beobachtungszahlen ebenso befriedigend wiedergibt wie die besten bisher aufgestellten Spektralgleiehungen, nämlich die von THIESEN [2]5), die von LUMMER-JAHNKE [4] und die von LUMMHR-PRINGS-HEIM [5]. (Wird an einigen Zahlen erläutert.) Ich möchte mir daher erlauben, Ihre Aufmerksamkeit auf diese neue Formel zu lenken, die ich vom Standpunkt der elektromagnetischen Strahlungstheorie aus nächst der WIENschen für die einfachste halte.
[1] M. PLANCK., Ann. Phys. 1 (1900) 730.
[2] M. THIESEN, Verh. Dtsch. phys. Ges. Berlin 2 (1900) 67.
[3] M. PLANCK, Ann. Phys. 1 (1900) 719.
[4] O. LUMMER, E. JAHNKE, Ann. Phys. Lpz. 3 (1900) 288.
[5] O. LUMMER, E. PRINGSHEIM, Verh. Dtsch. phys. Ges. Berlin 2 (1900)174.
*) Verh. Dtsch. phys. Ges. Berlin 2 (1900) 202.
1) Auch Hr. PASCHEN hat, wie er mir brieflich mitteilte, neuerdings merkliche Abweichungen vom Wienschen Gesetz festgestellt.
2) siehe [1], S.782.
3) Ich gehe aus von dem zweiten Differentialquotienten von S nach U, weil diese Größe eine einfache physikalische Bedeutung besitzt (s. [1], S. 731).
4) Der Ausdruck des WIENschen Verschiebungsgesetzes ist einfach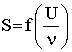 
wo ν die Schwingungszahl des Resonators bedeutet. Ich werde dies bei einer anderen Gelegenheit darlegen.
5) Man findet dort such bemerkt, daß Hr. THIESEN seine Formel schon aufgestellt hatte, ehe die Herren LUMMER u. PRINGSHElM ihre Messungen auf größere Wellenlängen ausdehnten, was ich hier hervorhebe, weil ich vor dem Erscheinen der zitierten Publikation eine etwas andere Darstellung gegeben hatte [3].