Wenn der ZP (Ziegelphysiker) seine Zitate (z.B. [26]), bezüglich des Werts von Aussagen [20] selbst Ernst nimmt, ist es unverständlich, daß die Autoren von [3] bis [5] Ihren Unsinn nicht selbst erkennen:
Karl Popper widerlegte die Überzeugung, es sei immer möglich ist, den Beweis zu erbringen, daß etwas wahr oder falsch ist. Popper zeigte, daß immer nur der Beweis dafür möglich ist, daß etwas falsch ist, während es sich nie letztgültig beweisen läßt, daß etwas wahr ist. Dies bedeutet, daß alle wissenschaftlichen Theorien, die wir für wahr halten, nicht deshalb als wahr betrachtet werden können, weil ihre Wahrheit wirklich bewiesen worden ist, sondern nur, weil es den Wissenschaftlern, die sie formuliert haben, gelungen ist, ihren Kollegen und uns glaubhaft zu machen, daß sie wahr seien. Normalerweise schließt das die Verwendung mehr oder weniger schwer wiegender Fälschungen und Tricks mit ein, die jedoch nicht als solche erkannt werden, oder wenn, dann erst nach langer Zeit.
Den Autoren von [3] bis [5] ist es gelungen, einigen ihrer Kollegen "glaubhaft zu machen, daß" ihr Unsinn wahr sei - und "die Verwendung mehr oder weniger schwer wiegender ... Tricks ..." passiert auch, siehe z.B. Abschnitt 2 Punkt 1). Außerdem ist es leichter Märchen zu erzählen als einen Fachbericht zu erstellen, der hat nämlich das Korsett der Wahrheiten.
Dabei ist der Beweis, daß die Behauptungen in [3] bis [5] fehlerhaft sind, z.B. in [9] und [22] erbracht - gemäß: "Um die Wirklichkeit der Welt, in der wir uns befinden, aufzuklären, ist diese kritisch-rationale oder hypothetico-deduktive Methode offenkundig unschlagbar." (aus [27] - auch zitiert von einem ZP). Nach diesem und dem vorhergehenden Zitat ist damit unschlagbar bewiesen, daß die Behauptungen in [3] bis [5] fehlerhaft sind.
Der Autor und andere verwenden diese zitierte unschlagbare Methode. Wenn der Nachweis der Gültigkeit des U-Wertes ([9] und [22]) falsch wäre, wäre das für die ZP gemäß deren eigenen Zitaten doch ein gefundenes Fressen diese Methode zu verwenden. Aber da auch für die ZP kein Fehler erkennbar ist, flüchten Sie in diffamierende Bemerkungen [4]: "Kann dies mit pseudologischen Tüftelein, verwirrenden Spitzfindigkeiten und scholastischen Etymologismen widerlegt werden?" oder beleidigend [5]: "Es wird keineswegs der Vorwurf erhoben, dass Maschinenbauer, Physiker und Elektriker die bautechnische Literatur nicht kennen, sondern nur, dass infolge ihrer opportunen Haltung ..."
Die ZP handeln aber selbst verwirrend. Unter der Überschrift "Berücksichtigung der Sonneneinstrahlung" steht der folgender Satz [5, S. 47]: "Die vierte Aussage: Sonneneinstrahlung bleibt unberücksichtigt. Feststellung: Gerade diese Annahme ist unrealistisch." mit der falschen Schlußfolgerung: "Der U-Wert muss wirklich ad acta gelegt werden ...". Ein Zitat zu diesem Sachverhalt [22, S. 10], vorletzter Absatz zur Berücksichtigung der Solarstrahlung]: "... siehe DIN V 4108-6: 200-11, Punkt 6.4.5 solare Wärmegewinne über opake Bauteile". In diesem Aufsatz [22] steht auch warum die Norm richtig ist. Ohne "verwirrenden Spitzfindigkeiten" usw. hätte ein Fachmann geschrieben: "... Feststellung: die enge Auslegung des Zitats hält neueren Erkenntnissen nicht stand".
Ist ein solches Verwirrspiel zu verstehen? Nehmen die ZP Argumente, die ihre Ansichten widerlegen, nicht zur Kenntnis oder verstehen sie diese nicht? Denn mit der richtigen Schlußfolgerung wäre viele Artikel überflüssig gewesen, z.B. [5]. Das Ganze ist um so unverständlicher, da sich die Werte aus den DIN-Formeln mit den schon lange bekannten Zahlen decken [28, S. 166, Table 6.10] und die ZP alte Arbeiten für richtig halten.
Es dürfte reizvoll sein, darüber nachzudenken, warum die ZP diffamierende Bemerkungen usw. schreiben anstatt ihre zitierte unschlagbare Methode zu verwenden.
Die Grundaussage der Artikel ist mit dem Wort "ominös" ja schon angedeutet: die ZP sind der Meinung, daß der U-Wert für irgendwelche Zwecke des Baus (speziell der Bauphysik) überflüssig, wenn nicht sogar falsch ist und behaupten, das bewiesen zu haben.
Die Numerierung hier folgt der Numerierung in [4].
- Die Materialkonstante Wärmeleitfähigkeit l
soll angeblich nur richtig sein bei konstanten Wärmestrom und um das zu unterstreichen, werden eigene Verwendungen bei instationären Vorgängen "vergessen":
- bei der Temperaturleitfähigkeit a ([3]: a =
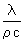mit r Dichte und c Speicherfähigkeit). - Die Nennung der Proportionalitätskonstante im Satz "... zu Wärmeströmen. Da diese sich proportional zum Temperaturgradienten verhalten ..." [4, Punkt 4)].
- c) daß die Fouriersche Wärmeleitungsgleichung die instationären Verhältnisse richtig beschreibt [5] - darin die wesentliche Materialkonstante l ([12], [31, Abschnitt 7]).
- bei der Temperaturleitfähigkeit a ([3]: a =
- Die Autoren behaupten fälschlich die Materialkonstante Wärmeleitfähigkeit l
wäre nur richtig bei konstanten Wärmestrom und um das zu unterstreichen, "vergessen" sie
- l bei der Temperaturleitfähigkeit a (siehe [3] a = 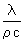mit r Dichte und c Speicherfähigkeit)
- im Punkt 4) im Satz "... zu Wärmeströmen. Da diese sich proportional zum Temperaturgradienten verhalten ..." die Proportionalitätskonstante l.
- daß der ZP in [5] sagt, daß die Fouriersche Wärmeleitungsgleichung die instationären Verhältnisse richtig beschreibt [12] - darin die wesentliche Materialkonstante l (siehe Abschnitt 7).
- l bei der Temperaturleitfähigkeit a (siehe [3] a =
-
- Entgegen des ZP Behauptung verhalten sich die Baustoffe selbst nicht instationär. Die instationären Temperaturen und Wärmeströme in den Baustoffen entstehen durch die instationären Beanspruchungen aus Umgebungstemperatur und Solarstrahlung. Diese feine Unterscheidung mag spitzfindisch klingen - aber illustriert das Verständnis des Geschehens durch ZP.
- Für den Bau und Nutzung geht es um den erforderlichen Aufwand für die Einhaltung des gewünschten Raumklimas (z.B. der Temperatur) - und dieser Aufwand wird durch die notwendige Heizleistung und Heizenergie und höchstens indirekt durch die Temperatur bestimmt.
- Bei instationärer Beanspruchung liegen im Bauteil im Allgemeinen tatsächlich unterschiedliche Wärmeströme vor. Aber die Schlußfolgerung bez. des U-Wertes ist trotzdem falsch:
- Temperaturgradient und Wärmestrom sind proportional (Proportionalitätskonstante l). Deshalb gleicht eine Diskussion, welche der beiden Größen wesentlich ist, dem Streit: was war zuerst da Huhn oder Ei?
- Der U-Wert ist zwar mit dem Beharrungszustand definiert, aber es ist schon mehrfach nachgewiesen (z.B. [9]), daß mit dem U-Wert die Wärmemenge bei ausreichend langer Zeit auch bei instationären Verhältnissen richtig ermittelt wird. Ein Streit darüber gleicht wieder "Huhn und Ei". Ein Beharrungszustand im "strengen Sinne" liegt praktisch nie vor (weil das Einschwingen unendlich lange dauert) und auch bei instationären Verhältnissen reicht eine genügend lange Zeit [32, Abschnitt 1].
- Bei Bestrahlung hängen die Temperaturen immer vom Absorptionsgrad ab. Die Glühfadentemperatur der beim "Lichtenfelser Experiment" verwendeten Lampe wird zwar nur ca. 3000 K sein. Das ist zwar nur die Hälfte der Sonnentemperatur, aber auch bei dieser Wellenlängenverteilung haben die verwendeten Materialien noch stark unterschiedliche Absorptionsgrade im Gegensatz zur Behauptung. Die ZP haben weder die Absorptionsgrade bestimmt noch jemals eine Nachrechnung gemacht, die nur mit unterschiedlichen Absorptionsgraden an die Meßkurven anzupassen ist. Auch für den Abfall der Temperatur der Mineralwolle [3, Abb. 2] erfolgt keine Erklärung. Wahrscheinlich kommt die warme Luft stärker in Bewegung und kühlt die Oberfläche.
- Der Aufwand für Heizen und Kühlen hängt vom Wärmestrom ab (siehe Punkt 3) - und da spielt die Verzögerung praktisch keine Rolle, da diese Zeiten groß gegen die charakteristische Zeit [32, Abschnitt 1] sind - im Gegensatz zum "Lichtenfelser Experiment" mit seinen 10 min.
- Die Antwort auf die Frage: "Wo bleibt die absorbierte Energie" ist im Wesentlichen falsch. Bei gleichen Innentemperaturen, gleicher absorbierter Energie und gleichem U-Wert ist der Anteil der Energie, die im Innenraum landet, auch gleich - der einzige Unterschied zwischen speicherfähigen und nicht speicherfähigen Bauteilen besteht in der Zeit, in der die Energie im Innenraum landet [28]. Der andere Teil wird wieder nach außen abgestrahlt.
- Die Autoren kennen scheinbar ihre eigene Veröffentlichung [3] nicht. Sonst hätten sie nicht "absurd" zum Wärmeverlust des Ziegels geschrieben, denn die ZP haben selbst gezeigt [3, Abb. 2], daß schon nach wenigen Minuten Abkühlung die Oberflächen der Dämmstoffe kühler sind als die Oberflächen der anderen Stoffe.
Eine Vorbemerkung: in [2] gibt der Autor eine Formel für den solaren Energiegewinn von Wänden an. Der Witz an der Formel ist, daß für Fall, daß die Sonne auch nachts scheinen würde (was man durch eine Bestrahlungslampe simulieren könnte), die notwendige Heizleistung steigt. Der Link, wo das nachgewiesen ist, kommt in Kürze (auf Langes Ziegelphysikseiten).
Nun Einiges zu [5]. Der ZP sucht sich veraltete Zitate heraus, um damit gegen den U-Wert zu polemisieren. Wie das erste Zitat in [5] (statt dem aus [24]) heute lauten würde, wurde dem ZP schon in einem eMail-Wechsel mitgeteilt [20]: "Folgendes ist vorauszuschicken: der k-Wert eines Bauteils wird mit dessen Wärmeverlust unter stationären, d. h. zeitlich unveränderlichen Randbedingungen definiert. Die Wärmespeicherfähigkeit und somit die Masse des Bauteils geht nicht in die Definition des k-Wertes ein. Bei instationären Bedingungen ist ein genügend langer Zeitraum zu betrachten, damit der Einfluß der Wärmespeicherung zu vernachlässigen ist. Der Einfluß der Solarstrahlung macht sich durch den Unterschied zwischen Oberflächen- und Umgebungstemperatur bemerkbar".
Ein über 20 Jahre altes Zitat zu benutzen und neuere Erkenntnisse zu ignorieren ist kein wissenschaftlicher Stil. Damit kann man den ersten Teil der Arbeit vergessen.
Die Interpretation des realen Temperaturverlaufs in der Wand zeigt Unverständnis [5, alle Abb.]. Z.B. ist in den Abb. 1 und 2 ein Beharrungszustand, ausgehend von der minimalen Temperatur eingezeichnet. Wenn der Beharrungszustand irgend etwas mit den realen Temperaturverläufen zu tun haben sollte, müßte die Kurve von einer mittleren Temperatur (den genauen Wert würde eine mathematische Analyse liefern) ausgehen. Um diese theoretische Beharrungskurve schwankt dann die reale Temperatur.
Und dann geht es wieder weiter mit dem Ignorieren wesentlicher Arbeiten [6], [7], [9] und mit mathematischen Unverständnis insgesamt: "Mathematisch (zu) vereinfachend: die Allgemeingültigkeit des U-Wertes". Was hat es mit der Fourier'schen Wärmeleitungsgleichung (WGL) auf sich? Für den ZP besteht die WLG immer nur rein aus der Gleichung selbst, daß zu einer Differentialgleichung vom Typ der WLG immer Rand- und Anfangsbedingungen gehören, scheint er nicht zu wissen*). Deswegen ist nur sein Punkt 1) a) (Wärmebilanz eines Volumenelements) richtig. Sein Punkt b) (Berücksichtigung von Wärmequellen) ist falsch, anstatt die äußere muß richtig stehen "die inneren Wärmequellen" (wie zum Beispiel die Hydrationswärme eines abbindenden Betons). Punkt c) (Speicherfähigkeit) ist richtig. Natürlich wird in der WLG auch die Solarenergie berücksichtigt - aber nicht als innere Quelle (und deswegen darf sie in der eigentlichen WLG nicht auftauchen - in der Wand ist es dunkel), sondern als die Randbedingung, denn die Sonne scheint auf die Oberfläche (Rand) der Wand - siehe auch [2, Abschnitt 6.5].
Punkt 2) (Temperaturverlauf in der Wand) ist richtig, aber schon Punkt 3) (Behauptung von Vereinfachungen) ist wieder falsch. 0 wird die Zeitableitung nur für spezielle Untersuchungen gesetzt (Untersuchungen zur Stationarität). Aber für allgemeine Untersuchungen ([7], [9]) - um die geht es bei der Relevanz des U-Wertes für den Heizbedarf - wird keine Stationarität vorausgesetzt und deswegen ist der zeitabhängige Term im Allgemeinen nicht 0 - also keine mathematische Vereinfachung und damit sind die anschließenden Punkte 4) bis 6) als Schlußfolgerung von Behauptung 3) falsch.
Für Punkt 6) [5] können die ZP den Leserbrief [22] nicht richtig gelesen haben. Sonst hätten sie nicht in aller Ausführlichkeit die unstrittige Definition des U-Wertes erläutert, aber kein Wort dazu verloren, daß in [9] nachgewiesen ist, daß der U-Wert bei langen Zeiten (siehe auch Abschnitt 1) den Gesamtwärmestrom richtig beschreibt. Und wieder eine falsche Aussage "Ein untrügliches Merkmal zeigt stets an, wann der U-Wert nicht einsetzbar ist: Die Temperaturkurve". Warum falsch? Weil zur Bestimmung der Temperaturkurve stets die komplette WLG (einschließlich Randbedingungen) zu benutzen ist und zum U-Wert selbst greift nur jemand, der die WLG nicht verstanden hat und deshalb die erforderliche Zeit [32, Abschnitt 1] einfach ignoriert.
Zwar könnte man das Wort "Gleichungssystem" im nachfolgenden Punkt a) dahingehend deuten, daß die ZP verstanden hätten, daß die WLG aus der eigentlichen Differentialgleichung und den Randbedingungen besteht - aber das Weitere zeigt, daß man mit dieser Deutung etwas richtiges hineininterpretiert, daß nicht existiert. Deswegen noch mal die Randbedingungen richtig erläutern: Zitat [2, S. 6.5 (41)]: " Die Strahlungsenergie I der Sonne wird entsprechend dem Strahlungsabsorptionsgrad as der Materialoberfläche gemäß Formel 6.5.12 absorbiert.". Und die Oberfläche ist der Rand der Mauer. Zum U-Wert einer Wand gehören immer noch die Wärmeübergangswiderstände an die Luft. Wird die Wand als geschichtetes System Luftschicht - eigentliche Wand - Luftschicht behandelt, entsteht ein kompliziertes Gleichungssystem, das für die einzelnen Schichten separat gelöst werden muß und dann über die Randbedingungen der einzelnen Schichten zusammengepaßt wird. Da aber das Speichervermögen der Luft vernachlässigt werden kann, vereinfachen sich die WLG für die beiden Luftschichten zu einem Widerstand. Damit ist das System WLG nur für die eigentliche Mauer zu lösen und damit ist die Randbedingung für die Mauer der Wärmeübergangswiderstand zur Umgebung plus Solareinstrahlung.
Damit sind des ZP Interpretationen der WLG in den Punkten a) (angeblich Nichtberücksichtigung der Solarenergie) und b) (angebliche Stationarität) falsch. Das komplette Gleichungssystem vernachlässigt nicht im geringsten die Solarenergie [23] - aber nicht im falschen Verständnis als innere Quelle in der Mauer, sondern richtig, d.h. die Solarstrahlung endet auf der Wandoberfläche (=Rand) und nicht in die Wand (lediglich beim Spezialfall einer trüben Glaswand wird Solarstrahlung in der Wand absorbiert und dann würde natürlich ein Term in der eigentlichen WLG dafür stehen). Punkt b) ist falsch, weil - wie schon erwähnt - im allgemeinen Fall der zeitabhängige Term wegen der Instationarität nicht 0 wird - im Gegensatz zur Behauptung. Richtig wird am Anfang von c) geschrieben: "Nur die Bearbeitung der allgemeinen Fourier'schen Wärmeleitungsgleichung mit Solarenergie führt zum Ziel" - und das ist in [6], [7] und [23] geschehen - aber das wird wieder nicht zur Kenntnis genommen, die Rechnung selbst nicht ausgeführt und frank und frei behauptet "In der 'offiziellen' Bauphysik ...." Solche Behauptung könnte bestenfalls für die DIN V 4108-6 zutreffen: Im Text der DIN wird auf Stationarität hingewiesen und dann im Weiteren instationär weitergearbeitet - das halte ich für unverantwortlich. Aus meinem Briefwechsel mit dem DIN entnehme ich, daß dieser Textfehler in Zukunft beseitigt wird - aber an dem Formelapparat ändert sich dadurch nichts, er hat nur eine saubere Grundlage.
Da eine exakte Lösung der WLG in [9] und [23] vorliegt, gehe ich gar nicht auf den Abschnitt "Dynamische Simulationsmodelle treffen nicht die Bau-Wirklichkeit" ein, obwohl da auch wieder Fehler sind und als "Beweis" wieder eine 20 Jahre alte Arbeit [24] herangezogen wird.
Der Anfang vom Abschnitt "Bautechnische Fakten falsch interpretiert" müßte eigentlich lauten: "Es ist der Vorwurf zu erheben, daß jemand, der ein Fachmann sein will neuere Literatur zum U-Wert konsequent ignoriert und deswegen unhaltbare Aussagen trifft." Statt dessen kommt eine Beleidigung (siehe Abschnitt 1).
- Der keff-Wert nach [2]
- trotz Verdopplung der Temperatur auch nicht einmal teilweise mehr nach außen abgegeben (sicherlich, weil der ZP glaubt, durch die Aufteilung der Strahlung zwischen innen und außen bereits alles getan zu haben) und
- ohne Temperaturgefälle nach innen befördert.
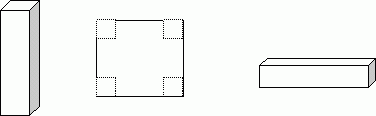
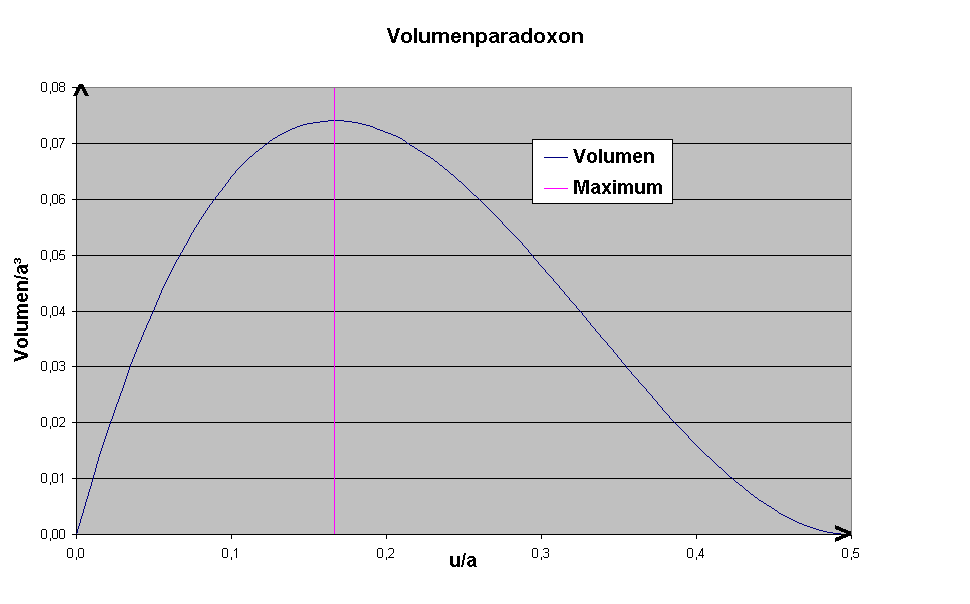
Bei vielen Dingen sind Optimierungen wichtig. Soll z.B. eine gegebene Dämmstoffmenge auf ein Gebäude mit zwei unterschiedlichen Innentemperaturen so verteilt werden, daß der Wärmestrom minimiert wird [18], so liegt ein Optimierungsproblem vor. Da Wärmeströme wenig anschaulich sind, wird das Prinzip einer Optimierung an einem anschaulischen Bauspiel erläutert. Dazu wird eine quadratischen Platte betrachtet, aus der eine Schachtel mit maximalen Volumen hergestellt werden soll. An den Ecken der Platte werden 4 gleiche Quadrate abgeschnitten und der Rest zu einer Schachtel hochgeklappt. Die Aussage: "paradoxerweise" hat die Schachtel bei niedriger oder hoher Höhe das gleiche Volumen ist analog der Aussage in [18], daß "paradoxerweise" bei verschieden Verteilungen der Dämmstoffmenge die Wärmeströme gleich sind. Zwischen den "paradoxen" Werten liegt sicher ein maximales Volumen der Schachtel bzw. ein minimaler Wärmestrom (Bild 4).
Bild 4: Volumenparadoxon - Volumen einer Faltschachtel
Der Beweis für das "Volumenparadoxon" ist in Abschnitt 6. In [18] ist kein Beweis des Optimums vorhanden, es fehlt sogar ein Hinweis darauf, wie das Optimum ermittelt wurde. Das Optimum ist zwar richtig, aber um das festzustellen, muß der Leser entweder dem Autor unbesehen glauben oder selbst das Wissen haben, daß die Abhandlung eigentlich vermitteln soll. Die Vermutung , daß bei so großen Mängeln und der hochtrabenden Wortwahl ("energetisches Paradoxon" für eine baupraktisch unwesentliche Optimierungsaufgabe) eine Vermutung als gesichertes Wissen verkauft wird, liegt nahe, da der ZP z.B. in [2, S. 13.1(87)] die Formel des Strahlungsaustauschs für eine unendliche Anzahl von Reflexionen zwar richtig ableitet, aber seine eigene Rechnung nicht versteht und dadurch [2, S. 13.1(91)] logische Widersprüche sieht, wo gar keine vorhanden sind. Hinweis zum Verstehen: auf Seite [2, S. 13.1(85)] hat der ZP unbewußt die Summenformel einer unendlichen geometrischen Reihe benutzt.
Alle Fehler in [2] aufzuzählen, die zu dem falschen keff geführt haben wird zu umfangreich, da es über 150 - fast immer - fehlerhafte Seiten sind. Da das keff als durchgehender Faden entwickelt wurde, sollte es reichen die Haltlosigkeit der Ableitung an einer Stelle zu zeigen. Aber durch Rückgriffe ist das Ganze so verwoben, daß man doch mehr aufzählen muß.
Das fängt mit 2 Begriffen an (Isotherme und Speicherquerschnitt): Bei der Temperaturverteilung im Mauerwerk gibt es Orte gleicher Temperatur. Die Gesamtheit dieser Orte werden üblicherweise als Isothermen bezeichnet. In [2] sind dagegen Temperaturkurven in einem Temperatur-Ort-Diagramm gemeint. Diese Kurven schließen mit den Achsen eine Fläche ein. Diese Diagrammflächen werden als Speicherquerschnitte bezeichnet. Es werden 3 Temperaturverteilungen benutzt: Temperatur konstant (bezeichnet als Rechteckquerschnitt), Temperatur mit linearer Änderung bei stationärer Temperaturdifferenz über einer Wand (Dreieckquerschnitt) und eine Temperaturverteilung mit einer quadratischen Parabel (Parabelquerschnitt). Diese letzte Temperaturverteilung liegt nie vor. Der ZP glaubt diese Kurve aus Abbildungen in [29] herauslesen zu können, obwohl das eher Summen von e-Funktionen sind und vergißt auch, daß die Temperatur auf der Wandinnenseite konstant gehalten wurde. Trotzdem wird diese unbegründete Annahme im weiteren für fast alle instationären Verhältnisse benutzt.
Von dem Vorigen ausgehend wird nun mit 2 hypothetischen Wänden weitergearbeitet. Vom realen Material soll die eine Wand nur das l ohne Speicherwirkung haben (c = 0) und die andere Wand keine Wärmeleitung haben (l = 0) und beide Wände sollen die gleiche Dicke haben und eine konstante Temperaturdifferenz über der Wand. Für die wärmeleitungsfreie Wand wird die gespeicherte Energie bei den angenommenen 3 Temperaturverläufen berechnet, für die andere Wand der Wärmestrom mit dem L-Wert (U-Wert ohne die Wärmeübergangswiderstände zur Luft). Und damit kann man verschiedene Fragen stellen: Wie lange dauert es, bei vorgegebener Dicke der Wände, bis in der U-Wert-Wand die gleiche Energie geflossen ist, wie sie in der Speicherwand gespeichert ist (Wärmeflußzeit)? Oder wie dick müssen die Wände bei vorgegebener Wärmeflußzeit für eine Bilanz sein?
Aber bei der Definition der Wärmeflußzeit ist keine Linie drin. Als Bilanzzeit mit hypothetischem konstanten Wärmestrom müßten für die 3 Fälle der Temperaturverteilung 1; 0,5 und 0,333 lauten, wird die Zeit genommen, in denen unter Benutzung der Ansätze in [30] (wie in [2]) näherungsweise die Hälfte der anfänglichen Wärme abgegeben ist, dann müßten die Zahlen mit ln(2) multipliziert werden, also 0,639; 0,347 und 0,231. Tatsächlich sind aber die angegebenen Zahlen 1; 0,347 und 0,206. Dafür wird die unsinnige Mischung hochtrabend mit "Die interpolative Approximation mit einer Exponentialfunktion von 0 über 0,347 nach 1 führt bei einem Parabelquerschnitt mit einer Drittelung des mitwirkenden Querschnitts zu einer 'Drittelwertzeit' von t1/3 = 0,206" beschrieben. Wie mit 0 in einer Exponentialfunktion (Grenzwert für Argument -¥) nach diesem Satzungeheuer umgegangen werden soll - ich versteh's nicht.
Speziell wird eine Wärmeflußzeit von 12 h angenommen [2, S. 6.5 (23f)]. Bis hierhin sind das nette nutzlose Spielchen, aber nur in Maßen falsch.
Aber nun wird es im Abschnitt 6.5.2.1.2 in [2, S. 6.5(41ff)] "Aufteilung der absorbierten Energien" direkt falsch. Zunächst kommen drei richtige Formeln (6.5.12, 6.5.13 und eine nicht numerierte Formel), die den absorbierten Anteil der Strahlungsenergie und dessen Aufteilung beschreiben und mit der DIN übereinstimmen. Aber dann wird für die Wand nicht die tatsächliche Wand genommen, sondern die Vorstehend genannte speicherlose Wand mit einer Dicke die sich aus der hypothetischen Wärmeflußzeit ergibt. Die für die Aufteilung an dieser speicherlosen Wand notwendige Temperatur interessiert nicht, sondern es wird der Wärmestrom genommen, der näherungsweise durch die speicherlose Wand fließt. Aber dann wird’s komisch. Die Wandtemperatur die wegen Absorption, Abstrahlung und Konvektion höher als die Lufttemperatur ist, wird auf einmal als Temperaturdifferenz infolge Außenlufterwärmung bezeichnet und gleichzeitig für weitere Rechnungen in der Wand verdoppelt, indem man das vorher verwendete L durch ein ks(24) ersetzt.
Und die "Merkwürdigkeiten" gehen weiter. Die einmal eingespeicherte Energie wird
Vor allen mit diesen 3 "Merkwürdigkeiten" kommt man dann auf den hohen Solarbonus.
Dabei geht es ganz einfach. Man sucht sich ein schönes Sommerwetter (von beispielsweise 14 gleichen Tagen) heraus und nutzt aus, daß die WLG eine lineare Gleichung ist, d. h. das eine Summe von Lösungen der WLG wieder eine Lösung der WLG ist. Für das Sommerwetter wird eine Fourierzerlegung (Gleichanteil plus Summe von periodischen Anteilen mit der Grundperiode 24 h) gemacht. Für periodische Lösungen ist die Lösung besonders einfach (siehe Abschnitt 8). Da für periodische Lösungen die Summation über eine Periode immer 0 ist, bleibt als Solargewinn nur der stationäre Anteil übrig - und der stimmt mit der DIN überein.
Wieso schreibt eigentlich ein ZP von einem "effektiven U-Werte" [2, Abschnitt 6.5], wenn er den U-Wert ad acta legen will? Allerdings wird mit diesem "effektiven U-Wert" der solare Gewinn um einen Faktor von ca. 2 bis 3 zu hoch berechnet (je nach Wandstärke usw.). Wäre die Berechnung richtig, hätten Massivhausbesitzer im Sommer eine durchschnittliche(!) Innentemperaturen von etwa 40°C!
Die Fehlerhaftigkeit mancher seiner Auslassungen müßte der ZP selbst erkennen. Angenommen man hat im Zimmer einen elektrischen Heizkörper. Ohne Strom wird er als kalt bezeichnet. Deswegen strahlt er trotzdem Wärme ab, wie man feststellen kann, wenn man diesen Heizkörper im Winter mit ins Freie nimmt. Im Zimmer erhält er aus der Umgebung genau so viel zugestrahlt, wie er abstrahlt (Temperaturgleichgewicht). Wenn der Heizkörper nun Strom erhält, strahlt er mehr ab und als Heizleistung erscheint die Differenz zwischen Gesamtabstrahlung und der Zustrahlung durch die Umgebung, die weiter in alter Höhe geschieht. Und nur diese Mehrleistung über der Abstrahlung des kalten Heizkörpers muß durch die zugeführte elektrische Leistung gedeckt werden. Das erkennt der ZP in einer Anmerkung zwar an [2, S. 13.1(54)], erklärt aber anschließend sofort diese Differenzbildungen für die Heizung als "unkorrekt", als ob man mit einem kalten Heizkörper einen Raum erwärmen könnte - das wäre ein Perpetuum mobile.
Für das Volumen (Grundfläche mal Höhe) der Schachtel (Bild 4) gilt:
( 1) V = (a - 2 u)2 u 0 £ u £ a/2
Bild 5: Volumenparadoxon
Sieht man sich die Kurve an, so ist zu sehen, daß das Maximum des Volumens bei u = a/6 eintritt. Deswegen erscheint folgender Ansatz für u zweckmäßig:
( 2) u = 
+ x -£ x £
Durch Einsetzen von ( 2) in ( 1) und einfache Umformungen¯) wird:
( 3) V = 4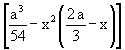
-£ x £
Da in dem zulässigen Bereich von x die runde Klammer in ( 3) immer > 0 ist, wird bei jedem x ¹ 0 das maximale Volumen von V = 4
= 2
nur verkleinert. Damit ist bewiesen, daß u = a/6 tatsächlich das maximale Volumen ergibt.
Mit cv als Volumenwärmekapazität:
( 4) cv = c r
wird als Ausgangspunkt folgende Form der Fourierschen Wärmeleitungsgleichung gewählt, die der ZP in [19] und [5] als richtig anerkennt:
( 5)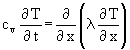 
Die Klammer in ( 5) beschreibt den Wärmestrom j richtig - siehe [4, Punkt 4)] (
ist der Temperaturgradient):
( 6) j = 
Gleichung ( 6) wird in Gleichung ( 5) eingesetzt. Das ergibt:
( 7) 
Gleichung ( 7) wird von einer Anfangszeit ta bis zu einer Endzeit te integriert. Dabei entsteht der Summenwärmestrom (mathematisch exakt das Integral des Wärmestroms), der ggf. durch die verbrauchte Heizenergie (Kühlenergie) gedeckt wird:
( 8)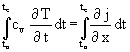 
Þ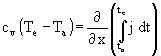 
Aus ( 8) ist jetzt das bekannte Ergebnis abzulesen: Ganz gleich wie der Wärmestromverlauf im Einzelnen war - wenn der Temperaturverlauf in der Wand zum Anfangs- und Endzeitpunkt gleich ist (z.B. Anfang und Ende der Heizperiode), ist die linke Seite in ( 8) gleich 0. Diese Tatsache verlangt, daß der Summenwärmestrom in der Wand konstant ist - anderfalls könnte der Gradient des Summenwärmestroms nicht 0 sein. Da der Wärmestromverlauf beliebig sein darf, darf z.B. auch die ganze Zeit der Beharrungszustand vorliegen. Da der ZP die Gültigkeit des U-Wertes im Beharrungszustand anerkennt, sollte er eigentlich auch die Gültigkeit des U-Wertes allgemein anerkennen.
Wenn am Anfang und Ende des betrachteten Zeitintervalls ungleiche Temperaturen vorliegen, ist natürlich die linke Seite von ( 8) nicht 0. Damit ist der summarische Wärmestrom innerhalb des Bauteils nicht konstant, sondern ändert sich im gleichem Maß, wie sich die im Bauteil gespeicherte Energie, nämlich cv (Te - Ta), ändert. Wenn der Summenwärmestrom groß genug ist, ist dessen Änderung durch die Speicherung zu vernachlässigen (siehe Abschnitt 9).
Nun könnte noch als spitzfindiger Einwand kommen, daß der Summenwärmestrom zwar konstant ist, im Beharrungsfall zwar mit dem U-Wert berechnet werden kann, aber das allgemein nicht zutrifft. Um diesen Einwand zu entkräften wird ( 7) wieder über das schon genannte Zeitintervall integriert:
( 9)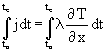 
Þ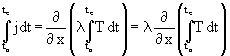 
Analog ( 9) die wird eine Summentemperatur S(t,x) als Integral (ein mathematischer Spezialfall der Summenbildung) der augenblicklichen Temperaturen in Anlehnung an [7] eingeführt. Speziell sind ist diese Summentemperaturen z.B. als Gradtagszahlen SG bekannt:
(10) S = 
oder speziell SG = 
Für das Einsetzen in ( 5) wird die Umkehrung der Integration, die Differentation gebraucht:
(11) T(t,x) = 
Diese Summentemperatur wird in die Fouriergleichung eingesetzt und es ergibt sich:
(12) 
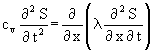
Diese Gleichung wird einmal nach der Zeit integriert:
(13) 
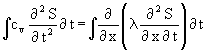Þ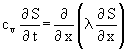 
D.h. für die Summentemperatur gilt formal die gleiche Gleichung, wie für die Temperatur selbst, womit der spitzfindige Einwand widerlegt wäre.
Zum Schluß diese Abschnittes noch der Spezialfall der homogenen Wand. Dann ist der Wärmeleitwert l konstant und die Fouriergleichung wird einfacher. Aus ( 5) wird:
(14) 
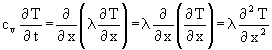
Nach Division durch c ergibt sich:
(15) 
Mit ( 4) zeigt sich, daß der Bruch in (15) der Temperaturleitwert a ist:
(16) a = 
=
Gleichung (16) wird in (15) eingesetzt und es ergibt sich die Fouriergleichung Wärmeleitungsgleichung (WLG) der homogenen Wand:
(17) 
Dazu wird eine streng periodische Temperaturfunktion betrachtet, die natürlicherweise instationär ist:
( 18) T = T0 + T1 * x + Tm * sin(wt - kx) e-kx
Dieser spezielle Temperaturverlauf wird in die WLG (17) (deren Gültigkeit sogar der ZP anerkennt - siehe Abschnitt 7) eingesetzt. Im Einzelnen ergeben dann die einzelnen Differenzierungsschritte:
( 19) Nach der Zeit: 
= Tm * w
* cos(wt - kx) e-kx
( 20) Nach dem Ort: 
= T1 + Tm * [- k * cos(wt - kx) e-kx - k * sin(wt - kx)e-kx]
= T1 - Tm * k *[cos(wt - kx) + sin(wt - kx)] e-kx
Und noch einmal nach dem Ort:
( 21) 
= 
= - Tm *k *{ [k * sin(wt - kx) - k *
cos(wt - kx)] e-kx -
- k * [cos(wt - kx) + sin(wt - kx)] e-kx}
= Tm * 2 k2 * cos(wt - kx) e-kx
Die letzte Zeile entsteht, weil sich die sin-Funktionen aufheben.
Werden nun die differenzierten Funktionen in die WLG eingesetzt, ergeben sich gleiche Größen auf beiden Seiten, wenn gilt:
( 22) w = 2 a k²
Aus dem angesetztem Temperaturverlauf ergibt sich der Wärmestrom j:
( 23) j = l * = l * { T1 - Tm * k
* [cos(wt - kx) + sin(wt - kx)] e-kx}
Trotz des einfachen Ansatzes, sieht der Wärmestrom noch kompliziert aus. Das vereinfacht sich aber, wenn man den Wärmestrom genau über eine Periode summiert (mathematisch genannt integriert). Das Integral von einer periodischen Funktion über eine Periodendauer ist nämlich immer Null. Daraus folgt:
( 24) Summe (j) = 
= l * T1 * Periodendauer
Und das Einfache: l * T1 ist genau der Wärmestrom nach dem U-Wert, der instationäre periodische Anteil spielt überhaupt keine Rolle.
Der Wärmestrom an der Oberfläche ist (z.B. wegen der Solarstrahlung):
( 25) j = l * = l * { T1 - Tm * k
* [cos(wt) + sin(wt)]}
- rechnerische Bestimmung der Grenze
Ausgegangen wird von folgender Gleichung in Abschnitt 8.:
( 26) w = 2 a k² woraus folgt: k =
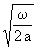
Zwischen w und der Periodendauer tp besteht folgende Beziehung:
( 27) w =
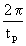
Die Speicherwirkung ist vernachlässigbar, wenn die Dämpfung der Wärmewelle infolge der Speicherwirkung vernachlässigbar ist, d.h. wenn
( 28) k 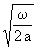x =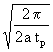
x = 
x =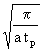 
x << 1ist. Daraus folgt durch Umstellung:
( 29) tp >>
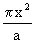
a ist ca. 5*10-7 m²/s für Ziegelmauerwerk, ca. 6*10-7 m²/s für Beton und 4 ... 15*10-7 m²/s für PS.
Damit wird für
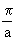: Ziegel 73 
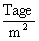Beton 61 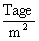PS 24 ... 91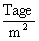 Bei Stärken um 20 cm (= 0,2 m) folgen daraus die Zeiten von mehreren Tagen, die wesentlich überschritten werden müssen, damit die U-Wert-Rechnung (ohne Berücksichtigung der Speicherwirkung) keine falschen Ergebnisse liefert:
Ziegel 3 Tage Beton 2,5 Tage PS 1 ... 3,6 Tage
Sehr schön kann man diese Verhältnisse durch eine Kurve darstellen, die die Wärmestromdichte als Zeitfunktion nach einer plötzlichen Temperaturänderung zeigt [32, Bild 1].
Diese Kurve kann man messen. Für den ZP muß man ergänzen: "sogar" messen. Aus der Kurve ist zu ersehen: unterhalb tp ist die Abweichung zwischen dem tatsächlichen Wärmestromdichten und dem U-Wert-berechneten sehr groß, bei Zeiten groß gegen tp aber klein.
Zusammengefaßt läßt sich Folgendes zum U-Wert sagen: Zur Berechnung eines aktuellen Temperaturverlauf muß immer die komplette WLG (einschließlich Randbedingungen) benutzt werden. Die verbrauchte Heizenergie ergibt sich immer aus der Heizenergieberechnung mit dem U-Wert allein + ein Teil der Änderung der in der Wand gespeicherten Wärme (der andere Teil der Änderung der gespeicherten Wärme geht in die Umgebung). Wenn zur Heizenergieberechnung allein der U-Wert benutzt werden soll, ist diese Berechnung nur für ausreichend lange Zeiträume richtig [9], damit der relative Fehler zur exakten Berechnung ausreichend klein ist. In der Regel reichen dafür ca. 14 Tage aus.
Der Beweis [9] geht von minimalen Vorkenntnissen zur Wärmeleitungsgleichung aus. Werden die Beweise von Weise [13, S. 299 - 312] (die Literaturstelle wurde von jemanden genannt, den Konrad Fischer als seinem Netzwerkpartner bezeichnet) verwendet, so wird der Beweis zur Allgemeingültigkeit des U-Wertes kürzer.
Wie Weizel [12] verwendet braucht natürlich auch Weise Anfangs- und Randbedingungen um Bweise zu führen.