In dieser Abhandlung wird ein ganz einfacher instationärer Fall auf der Basis von [58] und [65] behandelt, den jeder Fachmann nachvollziehen kann, selbst wenn er nur noch eine schwache Ahnung von Differentialgleichungen hat. Insbesondere Prof. Meier müßte das nachvollziehen können, denn er hat die Differentialgleichung in [58] dafür herangezogen, daß diese Differentialgleichung nicht richtig ausgewertet würde.

Deswegen zuerst ein ausführliches Zitat vom Anfang von [58], dem Brief Prof. Meiers (in blau - Überschriften usw. sind durch Punkte ersetzt. Formeln bleiben aber schwarz):

Zum Entwurf der

DIN 4108 "Wärmeschutz und Energieeinsparung in Gebäuden",
Teil 2: Mindestanforderungen an den Wärmeschutz

als Ersatz für die Ausgabe August 1981 und November 1995 wurde von mir (Prof. Meier) am 20. 07. 1999 folgende Stellungnahme an den NABau abgegeben:

Stellungnahme zur DIN 4108, Teil 2 vom Juni 1999

Bevor die Neufassung der DIN 4108, Teil 2, kommentiert wird, bedarf es der grundsätzlichen Klärung, inwieweit der k-Wert, der energetisch das gesamte Bauwesen beherrscht, Allgemeingültigkeit besitzt. Da jetzt mit der neuen Energieeinsparverordnung (EnEV) auch die Altbausubstanz "energetisch verbessert" werden soll, außerdem immer kleinere k-Werte gefordert werden (unwirtschaftlich) und darüber hinaus alle Nachweisverfahren des Wärmeschutzes den k-Wert zur Grundlage nehmen, wird diese Klärung notwendig. Vielleicht rennen wir einer Fiktion hinterher.

...

Wenn es um die Berechnung der Transmissionswärmeverluste und solaren Gewinne einer Außenkonstruktion geht, ... beruft man sich bei Grundsatzdiskussionen auf die Fouriersche Wärmeleitungsgleichung, die ja bereits seit 1822 bekannt sei.

Wie sieht diese Gleichung nun aus und in welcher Form leitet sich der k-Wert daraus ab?

Für den instationären Fall mit sonstigen Wärmequellen lautet die allgemeine Fouriersche Wärmeleitungsgleichung:

(1)(W/m³)

Wichtig für die wissenschaftliche Einordnung des k-Wertes wird allein die Kenntnis dieser fünf Bestandteile; die Formel (1) kann zur Orientierung in Kurzform auch wie folgt geschrieben werden:

(1a)(A) = (B) + (C) + (D) + (E)(W/m³)

Die einzelnen Summanden kennzeichnen folgende Bestandteile:

1. Links vom Gleichheitszeichen steht der Ausdruck, der die Speicherfähigkeit des Baustoffes beschreibt. Die darin enthaltene spezifische Wärmekapazität c [Wh/(kg K)] und das Raumgewicht r (kg/m³) sind hierfür die typischen Merkmale.
2. Rechts vom Gleichheitszeichen stehen drei gleichartige Ausdrücke, die die Wärmeleitung mit der jeweils darin enthaltenen Wärmeleitfähigkeit l (W/mK) berücksichtigen. Der erste Ausdruck gilt für die Wärmeleitung in x-Richtung (in Richtung der Dicke s).
3. Der zweite Ausdruck gilt für die Wärmeleitung in y-Richtung (quer zur Wand).
4. Der dritte Ausdruck gilt für die Wärmeleitung in z-Richtung (nach oben und unten).
5. Der letzte Ausdruck kennzeichnet sonstige innere Wärmequellen (mit Ergänzung richtig), wie z. B. die Solarstrahlung (falsch, zumindest nach Meier'schen Verständnis von E).

Das dreidimensionale Temperaturfeld wird nun zu einem eindimensionalen Temperaturfeld in x-Richtung reduziert. Es handelt sich dann um eine ungestörte Platte, in der nur eine Wärmestromrichtung vorliegt - von innen nach außen oder umgekehrt (B). Die Wärmeströme zur Seite (C) und nach oben/unten (D) werden nicht berücksichtigt. Diese Vereinfachung ist akzeptabel, obgleich damit die Wärmebrückeneinflüsse, die bei Schichtkonstruktionen besonders groß sind, eliminiert werden. Die Fouriersche Wärmeleitungsgleichung besteht somit nur noch aus drei Komponenten.

Diese reduzierte Form der Fourierschen Gleichung sieht dann in Differenzen-Schreibweise wie folgt aus:

(2)(W/m²)

In Kurzform sieht sie dann wie folgt aus:

(2a)(A) = (B) + (E)(W/m²)

Erläuterung der Formel (2):
Die rechte Seite beschreibt einmal die Differenz unterschiedlicher Wärmestromdichten (B), die bei instationären Verhältnissen immer auftreten (die Klammer enthält die Wärmestromdichte q) und zum anderen eine sonstige innere Wärmequelle (E) (mit Ergänzung richtig), wie sie z. B. bei der Solarstrahlung vorliegt (falsch, zumindest nach Meier'schen Verständnis von E). Die Wärmestromdifferenz und die sonstige Wärmequelle entsprechen dann der eingespeicherten Energie auf der linken Seite der Formel (A).

Entscheidend ist die Tatsache, daß bei instationären Verhältnissen der linke Ausdruck (A), der die Speicherfähigkeit eines Bauteils kennzeichnet, und v. a. die sonstigen inneren Wärmequellen (E) nicht weggelassen werden dürfen (falsch. In der Regel sind keine inneren Wärmequellen vorhanden. Die Behandlung der Sonne als innere Wärmequelle erfordert einen speziellen mathematischen Aufwand, und trotzdem ist E in der ganzen Wand Null außer einer ganz schmalen Schicht innerhalb der Wand, wo Luft und festes Material sich berühren). Dies jedoch geschieht, wenn der stationäre Fall weiterverfolgt wird.

Für den stationären Fall (Beharrungszustand) geht die allgemeine Fouriersche Wärmeleitungsgleichung (1) durch Nullsetzung in die Laplace-Gleichung (Potentialgleichung) über.

Damit wird deutlich:

Jeder der fünf Summanden (A) bis (E) wird zu Null (falsch: E muß für stationäre Verhältnisse nicht Null gesetzt werden.). Durch das eindimensionale Temperaturfeld in x-Richtung sind (C) und (D) bereits zu Null geworden. Für den Rest der Formel bedeutet dies im Klartext (s. Formel 2):

1. Die linke Seite der Fourierschen Wärmeleitungsgleichung (A), also die Speicherkomponente mit dem charakteristischen Speicherwert c , wird zu Null. Speicherfähigkeit wird somit völlig ignoriert (falsch, richtig wäre: spielt für stationäre Verhältnisse keine Rolle.).
2. Die Differenz zweier Wärmestromdichten in der x-Richtung wird auch zu Null (B). Wenn jedoch die Differenz an einer Stelle im Bauteil zu Null wird, dann muß überall die gleiche Wärmestromdichte vorliegen. Charakteristikum des Beharrungszustandes, des stationären Zustandes, ist also die konstante Wärmestromdichte mit geradlinigen Temperaturverteilungen.
3. Auch die sonstige Wärmequelle (E), wie z. B. die Solarstrahlung, wird zu Null. (falsch: E enthält die Solarstrahlung gar nicht.)

Durch Nullsetzung der Fourierschen Wärmeleitungsgleichung werden somit die Speicherfähigkeit der Außenbauteile negiert (A) (richtig: spielt in diesem Spezialfall keine Rolle), die konstante Wärmestromdichte im Bauteil erzwungen (B) und die Solarstrahlung ignoriert (E) (falsch: E enthält die Solarstrahlung gar nicht.).

Diese rigorose Vorgehensweise führt bei der Ableitung des k-Wertes, wenn nun für eine monolithische Konstruktion die entsprechenden Abmessungen und Temperaturdifferenzen eingesetzt werden, zu folgender Wärmestromdifferenz, die dann Null gesetzt wird:

(3)(W/m²)

Wird der k-Wert verwendet, dann wird:

(4)(W/m²)

Erläuterung der Formel (4):
Die eckige Klammer beschreibt die Wärmestromdichte q. Die Differenz ist Null. Dies bedeutet: die einem Volumenteilchen zugeführte Energie ist gleich der abgeführten Energie, die Wärmestromdichte q in W/m² ist somit im gesamten Bauteil konstant, die Temperaturlinie ist eine Gerade, Speicherung findet nicht statt.

Dieser konstante Wärmestrom q wird somit:

(5)(W/m²)

Erst diese stationäre Deutung des konstanten Wärmestromes q führt zu der in der DIN 4108 aufgeführten und nur für den Beharrungszustand geltenden Formel (liegen kurvige Temperaturlinien vor, so handelt es sich immer um instationäre Verhältnisse).

Von der ursprünglich aus fünf Komponenten bestehenden Fourierschen Wärmeleitungsgleichung verbleibt durch Nullsetzung nur eine Komponente übrig, die jedoch ausschließlich für stationäre Verhältnisse gilt. Dies ist dann der k-Wert, der das gesamte Bauwesen wärmetechnisch beherrscht und mit seiner Ausschließlichkeit förmlich stranguliert.

Nach der Abschweifung in den stationären Sonderfall im zweiten Teil des Zitats wieder die Rückkehr zur instationär gültigen Fouriersche Wärmeleitungsgleichung, indem bei Gleichung (2) weitergemacht wird.

Diese reduzierte Form der Fourierschen Gleichung sieht dann ohne Differenzen-Schreibweise wie folgt aus (und sogar ohne innere Wärmequellen, d.h. mit E = 0 - aber wie sich noch zeigt sehr gut auch für Solarstrahlung):

(2b)(W/m³)

Gleichung (2b) noch mal in besser lesbarer Form:

(2b)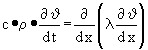

Für die weitere Behandlung wird die Gleichung (4) aus [65] benutzt, die zu einer besonders einfachen Betrachtung führt und hier die Nummer (6) erhält:

(6)

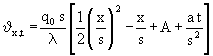
Dabei haben die einzelnen Größen in (6) folgende Bedeutung:

x: wie bisher die Ortskoordinate
s: die Dicke der Wand
A: eine Anfangskonstante, die willkürlich ist, aber an spezielle Verhältnisse angepaßt werden kann.
δ_x,t: Temperatur, die vom Ort (x) und der Zeit (t) abhängt.
t: Zeit
λ: Wärmeleitfähigkeit
a: Temperaturleitwert =
c: spezifische Wärmekapazität
ρ: Raumgewicht
q_o: Wärmestrom, dessen Bedeutung später klar wird.

Beim Einsetzen von (6) in (2b) sind mehrere Differentationen auszuführen. Damit auch Lesern, deren Beschäftigung mit der Differentialrechnung länger zurück liegt, den Ausführungen folgen können, wird jede Differentation einzeln ausgeführt und erklärt.

Der erste Schritt ist die Erklärung der Differentation. Dazu wird von einer Größe (z.B. Temperatur δ) ausgegangen, die sich um einen bestimmten Betrag (z.B. Δδ) ändert. Das Zeichen Δ steht dabei als Zeichen für eine Änderung. Für diese Temperaturänderung Δδ wird eine bestimmte Zeit Δt gebraucht. Die Geschwindigkeit der Temperaturänderung wird dabei durch den Bruch angezeigt - analog wie der Bruch zurückgelegte Fahrstrecke durch die dafür gebrauchte Fahrzeit die Geschwindigkeit des Fahrzeug anzeigt. Dabei ist es bei konstanter Geschwindigkeit gleich, wie groß man die Fahrtstrecke wählt, der Bruch bleibt konstant weil bei großer Fahrtstrecke auch eine große Zeit gebraucht wird. Wenn aber die Geschwindigkeit geändert wird, ändert sich auch der Bruch und die Geschwindigkeit wird durch diesen Bruch nur genügend genau angezeigt, wenn man eine genügend kurze Fahrtstrecke und genügend kurze Fahrzeit wählt. Dieser Bruch wird allgemein als Differenzenquotient bezeichnet. Mathematisch kann man die Differenzen sogar Null wählen, der Bruch 0/0 muß nur richtig behandelt werden, damit der Wert dieses Bruches wirklich den Wert des Differenzenquoutienten für die Differenz 0 annimmt.

Wie das geht, soll am Beispiel des freien Falls gezeigt werden. Die Fallstrecke y hängt von der Zeit wie folgt ab (g = Erdbeschleunigung):

(7) y = g t²/2

Wenn man die Fallstrecke eine kurze Zeit kurze Zeit Δt später betrachtet, ist die Fallstrecke y^*:

(8) y^* = g (t + Δt)²/2 = g (t² + 2 t Δt + Δt²)/2

Die zwischen (7) und (8) zurückgelegte Fallstrecke ist die Änderung Δy:

(9) Δy = y^* - y = g (t² + 2 t Δt + Δt²)/2 - g t²/2 = g (2 t Δt + Δt²)/2 = g Δ t (t + Δt/2)

Mit (9) kann nun der Differenzenquotient ermittelt werden:

(10)

Die Gleichung (10) ist die mittlere Fallgeschwindigkeit in dem Zeitabschnitt von t bis t + Δt. Wenn in (10) der Zeitunterschied Δt immer kleiner gewählt wird, geht der mittlere Ausdruck in 0/0 über, aber der letzte Ausdruck wird nicht 0/0 sondern g t/1 oder einfach g t. Nochmal geschrieben:

(11)

Die Fallgeschwindigkeit nimmt also proportional der Fallzeit zu.

Die Differentiale in (2b) sind mit (6) nicht komplizierter als die gerade eben durchgeführte Ermittlung der Fallgeschwindigkeit. Fangen wir mit der linken Seite von (2b) an:

(12)

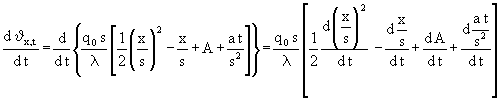
Wenn in (12) nach der Zeit differenziert wird, soll nur die Temperaturänderung als Folge der Zeitänderung betrachtet werden, während der Ort der gleiche bleibt. Das heißt, wenn man δ_x,t einen Moment Δt später betrachtet, hat sich δ_x,t zwar geändert - aber diese Änderungen werden nur durch Zeitänderungen verursacht - alle Terme, die nicht von der Zeit abhängen bleiben also unverändert. Das bedeutet, daß schon der Differenzenquotient Null ist und erst recht der Differentialquotient. Auf der rechten Seite trifft das auf die linken drei Summanden zu, nur der rechte ist zeitabhängig. Weil so viele Terme Null sind reduziert sich (12) auf:

(13)

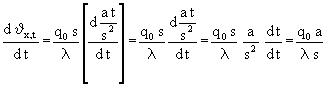
Analog ist bei der rechten Seite für x zu verfahren. Dabei wird mit der Differentation in der Klammer angefangen:

(14)

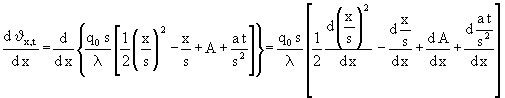
In (14) wird die Änderung von δ_x,t bei Änderung des Ortes betrachtet und die Zeit bleibt konstant. Deshalb bleiben alle Terme, die nicht vom Ort abhängen konstant und infolgedessen werden die Differentialquotienten Null. Damit verkürzt sich (14):

(15)

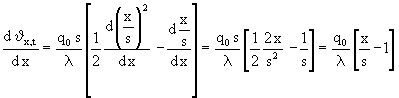
Nun ist (15) in die Klammer auf der rechten Seite von (2b) einzusetzen:

(16)

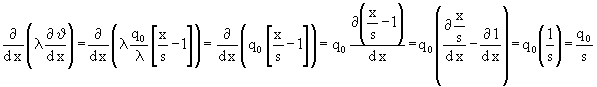
Nun sind (13) und (16) in (2b) einzusetzen:

(17)

Hält man sich nun die Definition des Temperaturleitwerts a vor Augen, so ergibt sich, daß mit dem Ansatz (6) die Differentialgleichung (2b) erfüllt ist. Das ist aber auch kein Wunder, denn der Ansatz (6) wurde so gewählt, daß die Differentialgleichung erfüllt wird. Damit ist der Ansatz (6) eine Lösung der Differentialgleichung. Dabei ist festzustellen, daß die Differentialgleichung bei jedem Wert von q_o erfüllt wird.

Interessant sind nun die Wärmeströme q in der Wand:

(18)

Das der Wärmestrom q proportional dem Temperaturgradienten ist hat Prof. Meier z.B. in [67] selbst geschrieben, nur hat er "vergessen" zu erwähnen, daß der Proportionalitätsfaktor eben λ ist. Der Temperaturgradient ist . Damit stellt (18) den Wärmestrom richtig dar.

An der Stelle x = 0 (Außenseite der Wand) fließt der größte Wärmestrom -q_o und nimmt zur anderen Wandseite (Innenseite der Wand) bei x = s auf 0 ab. Wo bleibt die in die Wand hineinfließende Wärme: sie wird natürlich in der Wand gespeichert und infolge der Speicherung kann immer weniger weiter fließen und ist dadurch auf der anderen Wandseite immer Null.

Die Lösung (6) der Fourierschen Wärmeleitungsdifferentialgleichung muß doch Prof. Meiers Herz höher schlagen lassen:

• Die Temperaturkurven sind Parabeln.
• In die Wand fließt ein konstanter Wärmestrom - und q_o kann man so wählen, daß es gleich der vom Material absorbierten Solarstrahlung I_s ist.
• Die absorbierte Solarstrahlung wird in der Wand gespeichert.

Allerdings wird die Lösung in den Augen von Prof. Meier einen Schönheitsfehler haben: sein Term E, der angeblich mit der Solarstrahlung identifiziert werden muß, wurde überhaupt nicht gebraucht.

Um die Lösung (6) zu Ende zu diskutieren, muß man jetzt die Randbedingungen ins Spiel bringen - eine Vokabel und Tatsache, die Prof. Meier offensichtlich nicht kennt. Und sicher aus dieser Unkenntnis folgt die beharrliche Behauptung, die Solarstrahlung würde nicht berücksichtigt, wenn E = 0 gesetzt wird.

Die Lösung hat (6) verlangt zweierlei:

• Die Oberflächentemperatur kann nur auf einer Seite und zu einer Zeit frei gewählt werden - und zwar durch Wahl von A.
• Auf der Innenseite der Wand darf kein Wärmestrom fließen. In [65] wird das dadurch erreicht, daß symmetrische Aufbauten gewählt werden.

Und diese Forderungen, die sich ergeben oder gewählt werden können, nennt man Randbedingungen. In der Regel ist der praktische Aufbau vorgegeben und damit auch die Randbedingungen. Für andere Randbedingungen als diejenigen, die sich aus (6) ergeben, ist (2b) auch lösbar - aber dann ist die Lösungsfunktion nicht mehr so einfach wie die Lösung (6) - oder man gibt wie in [65] und (6) die Lösungsfunktion vor - und muß dann die Randbedingungen so wählen, daß sich in der Praxis auch die gewünschte Lösungsfunktion einstellt.

Über Differentialgleichungen zu reden, ohne Randbedingungen zu erwähnen, hat die Qualität von Kaffeesatzleserei.

Literatur:

[58]	Meier, C.:	Stellungnahme zur DIN 4108, Teil 2 vom Juni 1999. Veröffentlicht von Prof. Meier in http://clausmeier.tripod.com/4108w.htm 20.07.1999
[65]	Krischer, O. und Esdorn, H.:	Einfaches Kurzzeitverfahren zur gleichzeitigen Bestimmung der Wärmeleitzahl, der Wärmekapazität und der Wärmeeindringzahl fester Stoffe. VDI-Forschungsbericht (Ausg. B) 21(1955) H. 450, S. 28 - 39.
[67]	Fischer, K. und Meier, C.:	Wärmedämmung. Bautenschutz und Bausanierung (B + B), 2003, H. 1, S. 12