Durch meine Veröffentlichungen sind Anfragen gekommen, deren Beantwortung vielleicht von allgemeinen Interesse ist. Deshalb die nachfolgenden Fragen und Antworten. Bei weiteren Anfragen wird die Liste ggf. erweitert.
Fragen:
Antworten:
1. Sehen Eigentümer und Mieter nach der Dämmung tatsächlich eine Einsparung?
Dazu ein Zitat "Es gibt nichts Praktischeres als eine gute Theorie." (Immanuel Kant / 1724 -1804).
Die Eigentümer haben nach der Dämmung schon eine Einsparung - aber aus dem hohlen Bauch ist die oft nicht erkennbar. Vielleicht kennen Sie als Leser den Versuch mit den 3 Schüsseln Wasser: links heißes, Mitte lauwarmes, rechts kaltes Wasser. Taucht man beide Arme eine Weile in die äußeren Schüsseln und geht anschließend mit beiden Armen in die mittlere Schüssel, so signalisieren beide Arme eine unterschiedliche Wassertemperatur, obwohl es doch mit Sicherheit die gleiche ist - und das weiß auch die Versuchsperson. Wissen und Gefühl klaffen sehr leicht auseinander.
Auch bei den Heizkosten täuscht das Gefühl leicht. In der Regel werden die Energiepreise laufend erhöht. Schon wenn die Energieeinsparung geringer ist, als die Erhöhung der Energiepreise stellt sich bei vielen das Gefühl ein, die Dämmung habe nichts gebracht - auf die Energiemenge, die auch auf der Rechnung steht, wird seltener geschaut.
Betrachten wir dazu z.B. das rechte Diagramm in der Kommentierung von Prof. Meiers Stellungnahme Punkt 21
Es liegt zweifellos eine Energieeinsparung durch die Dämmung vor. Sehen das aber die Eigentümer (Mieter) auch so? Vielleicht nicht. Warum?
Im Diagramm gibt es einen Punkt, der vor und nach dem Anbringen der Dämmung fast deckungsgleich ist - in dieser Heizperiode ist tatsächlich energieverbrauchsmäßig kein Vorteil eingetreten und wahrscheinlich sind nach der Dämmung sogar die Kosten höher, weil die Energiepreise inzwischen heraufgesetzt worden sind. Also ist die Kosteneinsparung von rund 12 % nur durch das Diagramm zu belegen - und da kann beim Eigentümer trotzdem ein falscher Eindruck bleiben - siehe Warmwasserversuch. Aber als Sachverständiger sollte man Wissen und Gefühl etwas trennen - obwohl das Gefühl öfters Hinweise geben kann, die dann aber mit Wissen zu untermauern sind. Wenn man das lange genug macht, nähern sich Wissen und Gefühl an - wie beim Autofahren, wenn man es kann, weiß man kaum noch, wie man es macht.
2. Gibt es einen Unterschied der Fouriersche Wärmeleitungsgleichung zur Realität und wie groß ist der ggf.?
Das Wärmeverhalten der Wände ist mit der Fourierschen Wärmeleitungsgleichung (WLG) zu beschreiben. Es gibt nur wenig, was mit dieser phänomenologischen Beschreibung (der Fourierschen Wärmeleitungsgleichung) nicht beschrieben werden kann. Diese WLG ist eine spezielle Form des Energieerhaltungsatzes: die WLG sagt nämlich, daß die zeitliche Änderung der gespeicherten Wärme gleich der örtlichen Änderung des Wärmestroms ist, d.h die Wärme die nicht weitertransportiert wird, wird gespeichert. Auch den zweiten Hauptsatz der Thermodynamik erfüllt die Gleichung. Dieser zweite Hauptsatz sagt, daß Wärme nur vom Warmen zum Kalten fließen kann und nicht umgekehrt. Im Zusammenhang mit einigen Fehlauslegungen dieses zweiten Hauptsatzes der Thermodynamik muß die Formulierung (nicht der Sachverhalt!) mit dem Wort "Netto" erweitert werden, also: "Der Nettowärmestrom ist immer vom Warmen zum Kalten gerichtet." Da bedeutet, es kann auch ein Wärmestrom vom Kalten zum Warmen fließen, aber der entgegengesetzte Wärmestrom ist immer größer.
Der Energieerhaltungsatz in direkter Form der Fourierschen Wärmeleitungsgleichung macht zwei weitere Voraussetzungen, die aber in den meisten Fällen mit großer Güte erfüllt sind: die gespeicherte Wärme ist proportinal der Temperatur und der Wärmeleitwiderstand ist temperaturunabhängig. Außerdem sollen weder die Proportionalitätskonstante (die Wärmekapazität) und der Wärmeleitwiderstand von nichts abhängen.
Noch eine Bemerkung: wenn die Wärme nur auf der Oberfläche einer Seite der Wand herauskommt, wäre das kein Perpetuum Mobile. Aber in der Realität wird es trotzdem nicht geschehen, daß die Wärme nur an einer Seite herauskommt (siehe Frage 4).
Strenggenommen hat die Lösung der WLG einige Unterschiede zur Realität, die aber so gering sind, wie die Beschreibung der Wand: Die Wand wird als homogen im Kleinen angenommen. Tatsächlich besteht sie aber aus Atomen. Und in der selben Größenordnung sind die Abweichungen zwischen Realität und Rechnung. Z.B. nennt die Lösung der WLG bei einem Temperatursprung auf der einen Seite eine sofortige Reaktion auf der anderen Seite der Wand, was in der Realität nicht zutrifft - aber dies Änderung ist Null, wodurch eigentlich kein Unterschied zwischen Rechnung und Realität vorliegt.
3. Wie sind die atomaren Grundlagen der Fourierschen Wärmeleitungsgleichung?
Da gibt es oft Mißverständnisse. Das fängt schon bei der oft verwendeten Formulierung "stoßen die Atome (Moleküle) die Nachbaratome" an. Atome sind keine Billardkugeln, die sich gegenseitig anstoßen. Atome sind hauptsächlich leerer Raum und können einander durchdringen.
Die Aufenhaltswahrscheinlichkeit der Elektronen eines Atoms kann sehr weit vom Atomkern weg sein, bei Metallen sind die äußeren Elektronen sogar teilweise so weit entfernt, daß sie einem bestimmten Atom gar nicht mehr zugeordnet werden können - man spricht dann vom Elektronengas. Daraus ist zu ersehen, daß sich die Atome gar nicht anstoßen können. Mehr fixiert sind die Orte der Atomkerne. Die Fixierung der Orte geschieht hauptsächlich durch elektromagnatische Kräfte. Wenn sich 2 Atomkerne (positiv) zu nahe kommen, ist die Abschirmwirkung der Elektronenhüllen (negativ) wegen der Durchdringung geringer und die Kerne stoßen sich ab. Ganz so einfach ist es aber auch nicht, sonst müßten alle Stoffe als einatomige Gase vorliegen. Wenn sich zwei Atome nahekommen, ist es oft energetisch günstiger oder sogar nur zulässig (sogenanntes Pauliprinzip in der Quantentheorie), daß die Elektronen benachbarter Atome beide Atomkerne gemeinsam umkreisen. Dadurch entsteht eine gewisse Anziehungskraft.

Bei kleinen Abständen, bei denen die Potentialkurve abfällt, herrscht Abstoßung, bei größeren Abständen steigt die Potentialkurve an und dehalb herrscht Anziehung. Wie man sieht, gibt es eine bestimmte Entfernung (R0), wo weder Anziehung noch Abstoßung herrscht (waagerechter Teil der Kurve) - das ist die Ruheentfernung.
Daneben gibt es auch Atome, die sich nicht mögen - und zwar dann, wenn die Drehrichtung (Spin) der Elektronen beider Atome gleich ist. Da man ein Elektron schlecht sehen kann, kann man auch die Drehung der Elektronen nicht sehen und spricht deshalb einfach vom Drehimpuls oder Spin der Elektronen.
Damit ist das beste Modell des Festkörpers hinsichtlich Wärmeleitung: Massenpunkte (Atomkerne), die durch Federn verbunden sind, wobei die Ruhelänge der Federn gleich den Atomabständen ist.
Bei Wärmebewegung bewegen sich hauptsächlich die Atomkerne um ihre Ruhelage und beeinflussen durch ihre Bewegung aus der Ruhelage über die Federn die Nachbaratomkerne.
Wie stark ist nun die Bewegung aus der Ruhelage? Genaugenommen stehen jedem Atom 6 sogenannte Freiheitsgrade zur Verfügung: das Zusammendrücken der Feder (potentielle Energie) und die Bewegungsenergie des bewegten Atomkerns (kinetische Energie) - und das in den 3 Raumrichtungen. Nun haben die Messungen gezeigt, das jeder Freiheitsgrad bei Erwärmung immer kT/2 an Energie aufnimmt (k=1,38*10-28 Ws/K, T absolute Temperatur). Bei N Molekülen je kmol (1 kmol = so viele Kilogramm eines Stoffes wie das Atomgewicht der Atome) ist also die Gesamtenergie E = N*6*kT/2 = 3 N k T = 3 R T, mit R = N k = 8314 Ws/(K kmol). Als obere Grenze bei hoher Temperatur wird das bei allen Festkörpern erreicht:
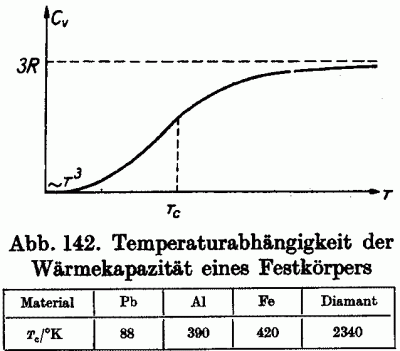
Das ist die Regel von Dulong-Petit oder hier.
Aber bei niedrigen Temperaturen (im Bereich von Tc und niedriger) werden diese Werte nicht erreicht. Je härter, um so steifer sind die Federn und um so höher ist Tc und auch die Schallgeschwindigkeit. Baustoffe haben in der Regel ein Tc, das weit unter den Einsatztemperaturen liegt.
Dieses Verhalten c(T), läßt sich leicht mit der Quantentheorie erklären (Debyesche Theorie), man spricht dabei von eingefrorenen Freiheitsgraden. Das hängt damit zusammen, daß gemäß Quantentherie die Energie nicht beliebig klein sein kann, sondern die Energie bei jeder Schwingungsfrequnz nur "stückweise" vergrößert werden kann. Deshalb muß eine bestimmte Mindestenergie vorhanden sein, um überhaupt eine Schwingung anstoßen zu können. Das man in der Regel trotzdem eine glatte Kurve mißt, hängt damit zusammen, das viele Schwingungsfrequenzen in Abhängigkeit von der Schwingungsart möglich sind: alle Atome im Festkörper können gleichzeitig fast in die gleiche Richtung schwingen bis zu benachbarten Atomen, die entgegengesetzt schwingen.
Auch die Wärmeausbreitung ist damit zu erklären: Eindringende Wärme wird zuerst die Atome nahe der Oberfläche in stärkere Unruhe versetzen, über die Federwirkung wird dann die Unruhe weitergereicht.
4. Perpetuum Mobile und Richtung des Energieflusses
Energie kann nicht verlorengehen, denn zu einem Prozeß gibt es in der Regel auch den umgekehrten Prozeß. Wenn also Energie verloren gehen könnte, könnte auch Energie aus dem Nichts entstehen - und dann gäbe es auch Perpetuum Mobile.
Also wird Wärme, die auf einer Seite in die Wand gebracht wird, sich auf 3 Anteile verteilen:
Wie die Aufteilung der eingebrachten Wärme ist, hängt von den Randbedingungen an der Oberfläche ab. Wenn die Wand sehr dick ist, muß eine Seite schon sehr lange erwärmt werden, damit ein merklicher Teil der eingebrachten Wärme die andere Seite erreicht, der größte Teil wird in einer dicken Wand gespeichert. Wird dann mit der Erwärmung aufgehört, wird ein großer Teil der Wärme die Wand auf der Seite verlassen, auf der sie eingebracht wurde.
Bei einer 24-Stunden-Periode (geringe Eindringtiefe) wird bei einer dicken Wand fast nichts davon auf der anderen Seite bemerkbar sein.
5. Wie wirkt sich die Reibung bei der Wärmebewegung aus?
Was bedeutet Reibung? Auch bei der Reibung geht keine Energie verloren, sondern eine "gerichtete" Energie wird in alle Richtungen zerstoben. (Anmerkung: Energie hat natürlich keine Richtung, aber der "Energieträger"). Wenn z.B. ein Ball durch die Luft fliegt, werden Luftmoleküle angestoßen und fliegen in verschieden Richtungen, stoßen wieder andere an und wieder wird die Energie aufgeteilt und in neue "Richtungen" verteilt, bis sich schließlich alle gegenseitig unregelmäßig anstoßen - aus der Energie, die gebraucht wird um die Reibung zu überwinden ist schließlich Wärmebewegung oder kurz gesagt "Wärme" geworden.
Bei der Wärmebewegung liegt ja schon eine ganz unrelmäßige Bewegung vor. Durch "Reibung" kann die Bewegung nicht noch unregelmäßiger werden, weil schon eine maximale Unrelmäßigkeit vorliegt - deshalb spielt bei der Wärmeausbreitung die Reibung keine Rolle.
6. Warum dämmt ein Material besser oder schlechter als ein anderes?
Um so weicher die Federn sind, um so langsamer wird die Ausbreitung heftiger Unruhe von einer Stelle zu einer anderen sein. Wenn gar keine Federn vorhanden sind (Gas) ist die Wärmeleitung besonders niedrig, weil die Wärmeleitung allein durch Zusammenstöße erfolgt - aber auch das wieder nicht als Billardkugeln, sondern als Abstoßung, wenn die Atomkerne sich zu stark nähern. Bei Gasen ist ja der mittlere Abstand der Atome bzw. Moleküle groß gegenüber dem Abstand in Festkörpern.
Metalle sind besonders gute Wärmeleiter, weil die Energieausbreitung nur zum Teil über die "Federn" erfolgt, der größte Teil wird über das Elektronengas vermittelt - wegen der geringen Masse der Elektronen erfolgt das besonders schnell.