Dipl.-Physiker Jochen Ebel
Oberfläche und Speicherung (Kurzfassung)
Inhaltsverzeichnis
0. Vorbemerkung
1. Aufstellung der Gleichungen
1.1 Anwendung der Laplace-Transformation
2. Lösung der Gleichung
3. Darstellung der normierten Temperaturfunktion
4. Schlußfolgerungen
5. Literatur
Dieser Artikel ist eine Kurzfassung von [1], der mehr mathematisch orientiert ist als diese Kurzfassung. Das geht schon aus dem umfangreicheren Überschriftenverzeichnis vor:
1. Aufstellung der Gleichungen
1.1 Anwendung der Laplace-Transformation
2. Lösung der Gleichung
2.1 Rücktransformation
2.1.1. Rücktransformation mit Tabelle
2.1.2. Überprüfung durch Reihenvergleich
2.1.3. Überprüfung durch Transformation
2.2 Reihenentwicklung für große Zeiten
2.3 Reihenentwicklung für kleine Zeiten
2.4 Asymptotische Lösung
2.5 Gewichtsfunktion und Lösung mit Reihen
2.5.1. Gewichtsfunktion und Lösungsansatz
2.5.2. Ansatz und und Lösung der Reihe
2.5.3. Fehlergrenzen der Reihe
3. Darstellung der normierten Temperaturfunktion
3.1 VBA-Basic zur Reihenberechnung
3.2 Diagrammdarstellung
4. Schlußfolgerungen
5. Literatur
1. Aufstellung der Gleichungen
In [2] wurde nachgewiesen, daß der Zeitverlauf der Oberflächentemperatur allein bestimmend ist für die Wärmespeicherung in der Wand bei gegebenen Aufbau. Offen geblieben ist die Frage nach dem Zusammenhang zwischen Oberflächentemperatur und den Umgebungsbedingungen. Das Problem kann hier nur für wenige Spezialfälle gelöst werden, aber damit kann für viele Fälle der Einfluß abgeschätzt werden.
Eine wichtige Rolle dabei spielt der Begriff des Gleichgewichtes. Wenn sich die Umgebungsbedingungen laufend ändern, ist es schwer bis unmöglich, den momentanen Abstand zum Gleichgewicht zu bestimmen. Deswegen wird der hier nur ein Spezialfall untersucht: In einer Umgebung, die für alle Zeiten eine Temperatur von 0°C hat, befindet sich eine ∞ dicke Wand, die für die Zeit t < 0 auch die Temperatur 0°C hat, ab der Zeit t = 0 soll eine konstante Strahlung mit dem nichtreflektierten Anteil E einfallen. Dieser hat in SI-Einheiten die Dimension W/m².
Gesucht wird die Oberflächentemperatur der Wand. Dabei ist zu berücksichtigen, daß es bei steigender Wandtemperatur T zum Wärmeverlust in die Umgebung kommt. Für Zeiten < 0 sollte ja Gleichgewicht herrschen, d.h. abgestrahlte und empfangene Wärmestrahlung waren gleich. Ohne wesentliche Einschränkung der Allgemeinheit wird angenommen, daß der bei Temperaturerhöhung eintretende Wärmeverlust proportional der Temperatur ist (siehe Gleichung (22) und (23)). Damit wird ein Verlustkoeffizient ε (mit etwas anderer Bedeutung gleich dem Wärmeübergangskoeffizienten) definiert, der nur von der Art der Oberfläche abhängig ist, aber unabhängig vom weiteren Aufbau der Wand (siehe z.B. [5]). Dieser hat in SI-Einheiten die Dimension W/m²K. Der Wärmestrom im Wandinnern wird q genannt. Dieser hat in SI-Einheiten die Dimension W/m². Aus der Definition der Wärmestromrichtung in [2] ist für q ein "-" zu berücksichtigen. Damit entsteht folgende Gleichung:
| (1) | E - ε T = -q |
Bei [2, Gl. (17)] ergibt sich bei Berücksichtigung der Voraussetzung, das T(t) für t < 0 gleich 0 sein soll, daß die obere Integrationsgrenze nicht bis ∞, sondern nur bis t reicht. Mit der modifizierten [2 , Gl. (17)] ergibt sich aus (1):
| (2) | E - ε T(t,0) = -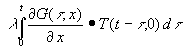 |
Wegen der vorausgesetzten dicken Wand ist aus [2, Gl. (16)] auch die Funktion G bekannt. Dabei hat a in SI-Einheiten die Dimension m²/s:
| (3) | E - ε T(t,0) = -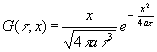 |
mit |
Um (3) in (2) einsetzen zu können ist (3) nach x zu differenzieren:
| (4) | 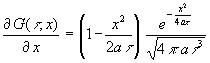 |
mit |
Wird außerdem noch berücksichtigt, daß die Oberflächentemperatur interessiert und dort x = 0 ist, vereinfacht sich (4) (die e-Funktion wird damit = 1):
| (5) | mit |
Nun kann (5) in (2) eingesetzt werden:
| (6) | E - ε T(t,0) = -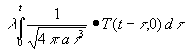 |
mit |
![]() als Konstante kann vor das Integralzeichen gezogen werden. Der Quotient mit λ ist als Wärmeeindringskoeffizient b bekannt [4]. Dabei hat b in SI-Einheiten die Dimension Ws½/m2K:
als Konstante kann vor das Integralzeichen gezogen werden. Der Quotient mit λ ist als Wärmeeindringskoeffizient b bekannt [4]. Dabei hat b in SI-Einheiten die Dimension Ws½/m2K:
| (7) | b = |
Mit (7) wird aus (6):
| (8) | E - ε T(t,0) = -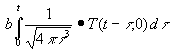 |
(8) ist eine Volterragleichung 2. Art [6, S. 4ff] zur Bestimmung der unbekannten Funktion T.
1.1 Anwendung der Laplace-Transformation
Vorstehende Aufgabe wird zweckmäßig mit der Laplacetransformation behandelt, siehe [3] oder [4, S. 94ff]. Zunächst wird der Kern in (8) transformiert. Dafür ist keine Bildfunktion in der Tabelle [8, S. 227ff] vorhanden. Unter Nr. 3.1 ist ein Transformationspaar aufgeführt, Mit dem weitergearbeitet werden kann:
| (9) |
Nach dem Differentationssatz der Laplacetransformation wird daraus:
| (10) | 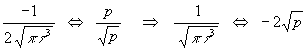 |
Mit dem Faltungssatz der Laplacetransformation und der Laplacetransformierten der Konstante E wird aus (8) mit (10):
| (11) |
(11) hat die Form einer algebraischen Gleichung und wird nach TL aufgelöst:
| (12) | TL = E 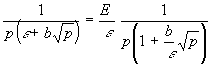 |
Zunächst aus Dimensionsgründen wird folgende Zeit tN definiert, aber später zeigt sich, daß das eine sehr gute Bezugszeit ist:
| (13) |
Damit wird aus (12):
| (14) | TL = |
Am Einfachsten ist die Rücktransformation durch Rückgriff auf eine Tabellensammlung. Wegen der Wurzel im Nenner ist dieses Transformationspaar nur in umfangreichen Sammlungen zu finden, z.B. [8]. In [8, S. 229] ist unter Nr. 3.22 das gesuchte Transformationspaar zu finden:
| (15) | mit | 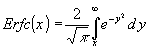 |
Allerdings ist in [8] ein Druckfehler (das "e" wurde vergessen). In [1] ist nachgewiesen, daß (15) richtig ist. Um (15) in (14) einsetzen zu können wird zunächst (14) mit a, das hier nach Vergleich mit (14) den Wert ![]() hat, multipliziert, so daß:
hat, multipliziert, so daß:
| (16) | 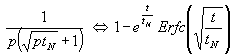 |
mit | 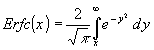 |
entsteht. Mit (16) folgt aus (14):
| (17) | T = 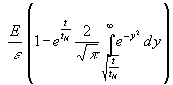 |
Mit einer zweckmäßigen Normierung, die die Allgemeingültigkeit deutlicher macht:
| (18) | t = tN x und T(t) = T(tN x) = |
wird aus (17):
| (19) | y(x) = 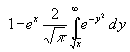 |
Eine Tabellierung dieser Funktion ist dem Verfasser unbekannt. In [1] ist dies durchgeführt und noch eine Näherung angegeben:
| (20) | yK(x) = 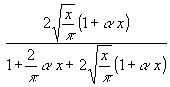 |
Für α ist ein Wert von ≈ 0.69 optimal und hält den maximalen Differenzfehler zwischen exaktem und Näherungs-Wert unter 0,011.
Zwar sind ex und Erfc(x) tabelliert, aber die Berechnung der Werte zur Darstellung ist aufwendig, da nur wenige Rechner die Funktion Erfc(x) direkt haben (z.B. bei Statistikprogrammen). Bei den meisten Rechnern müßte deshalb ein Programm zur Berechnung von Erfc(x) installiert werden. Dann aber ist es besser ein Programm zur direkten Berechnung von (19) zu installieren. Derartige Programme beruhen auf Reihenentwicklungen der zu berechnenden Funktion. Für (19) sind in [1] die Reihen entwickelt worden und ein Programm zur Berechnung dieser Reihen. Dabei mußten 2 Reihen entwickelt werden, eine für kleine Zeiten (bis etwa 13 tN und eine für große Zeiten. Außerdem gehört dazu die Abschätzung der Ungenauigkeit sowohl durch den notwendigen Abbruch einer ∞ langen Reihe als auch durch die beschränkte Rechengenaugkeit infolge der interne Zahlendarstellung im Computer.
3. Darstellung der normierten Temperaturfunktion
Damit sind nun die Grundlagen geschaffen, damit y und yK (Gl. (20)) tabelliert und als Diagramm dargestellt werden können. Im allgemeinen wird es reichen, die graphische Darstellung des Funktionsverlaufs zu sehen.
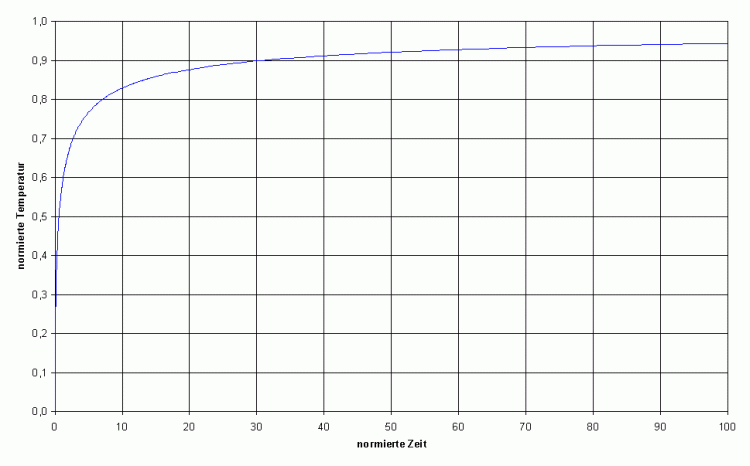
Bild 1: normierter Temperaturverlauf über normierter Zeit
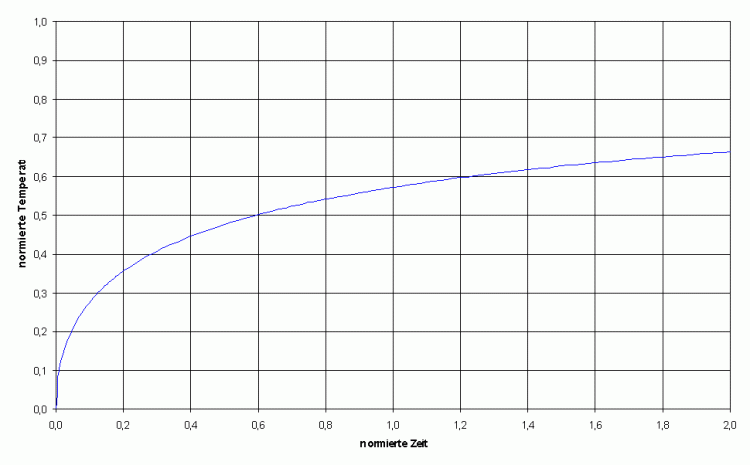
Bild 2: Auszug aus Bild 1 für kleine Zeiten
Für Zeiten t << tN (normiert << 1) ist der Wärmeleitungsvorgang weit vom Gleichgewicht entfernt, d.h. der Wärmeverlust durch Erhöhung Oberflächentemperatur ist klein gegenüber der Einstrahlung.
Für typische Materialien ist nun tN zu bestimmen. Zuerst wird ε bestimmt. Wird für ε der schwarze Strahler genommen {mit TU Umgebungstemperatur, ΔT der Temperaturerhöhung,
| (21) | σ = 5,67•10-8 W/m2 K4) |
wird die Energieabstrahlung E*. Dabei muß berücksichtigt werden, das die Oberfläche nicht nur Energie abstrahlt, sondern auch von der Umgebung Energie zugestrahlt bekommt.
Anmerkung: Für den Namen von σ ist "Stefan-Boltzmann-Konstante" am gebräuchlichsten. Daneben gibt es noch den Namen "Stefan-Konstante" [13, Seite 665: "universelle Stefan-Konstante", Seite 862: "Stefan-Boltzmann", Seite 887: beide]. Das ist erklärlich, denn Stefan hat 1879 [10] das T4-Gesetzt herausgebracht, Boltzmann hat das 1884 [11] ergänzt. Die DIN [14] nennt keinen Namen .
Im Zustand vor Einschalten der zusätzlichen Strahlungsquelle E (siehe (1)) hatte die Oberfläche genausoviel Energie empfangen, wie sie selbst abgestrahlt hat (Gleichgewicht), d.h. E* war 0. Deswegen wird zweckmäßig die Temperatur der Oberfläche als Summe von Umgebungstemperatur und Temperaturerhöhung angesetzt:
| (22) | E* | = σ (TU + ΔT)4 - σ TU4 = σ (4TU3 ΔT + 6TU2 ΔT2 + 4TU ΔT3 + ΔT4) |
= σ 4TU3 ΔT {1 + 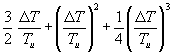 } } |
Bei den interessierenden Temperaturdifferenzen sind die Brüche in der geschweiften Klammer so klein gegen 1, das sie vernachlässigt werden können. Daher wird für E* nur der in ΔT lineare Anteil genommen und mit (1) wird:
| (23) | E* = σ 4 TU3 ΔT = ε ΔT |
Für TU = - 10°C = 263 K wird aus (23) mit (21):
| (24) | ε = 5,67 10-8 W/m2 K4 × 4 × 2633 K3 = 4,12 W/m2 K |
In [5] ist eine ähnliche Linearisierung vorgenommen worden. Ist die Oberfläche nicht schwarz (d.h. der Reflexionskoeffizient ist wellenlängenunabhängig = 0), sonder farbig (d.h. der Reflexionskoeffizient ist wellenlängenabhängig > 0) wird ε kleiner, kommt Konvektion und Wind dazu, wird ε größer. In [4, S. 143ff] ist b für verschiedene Stoffe angegeben, ausgewählt werden hier Kiesbeton (b = 1570 Ws½/Km2) und ein Styropor-Schaumstoff (mittlerer Wert b = 49 Ws½/Km2). Mit diesen Werten und (13) wird für tN:
| (25) | Beton: 145212,79 s = 40,3 h | Polystyrol: 141,45 s = 2,35 min |
Beide Werte sind aus 2 Gründen nur Orientierungswerte: 1. Man hat es in der Praxis nicht mit ∞-dicken Wänden zu tun und 2. die Oberfläche besteht nicht nur aus einer ganz dünnen Oberflächenschicht, die für die Wärmeleitung unwesentlich ist, sondern hat eine gewisse Stärke. Wird der tägliche Wetterverlauf (mit typischen Zeiten um Stunden) betrachtet, so ist aus (25) trotzdem abzuschätzen, daß die Oberfläche von Betonwänden der fiktiven Umgebungstemperatur (Lufttemperatur plus Strahlungseinfluß, in [5] kritisiert Sonnentemperatur genannt) kaum folgt. Im Gegensatz dazu macht die Oberfläche einer Dämmstoffwand alle Temperaturbewegungen mit. Anders sieht es mit Witterungstrends aus (typischen Zeiten um Tage). Diesem Trend folgen etwa die Oberflächen beider Wände.
Obenstehende Lösung folgt weitgehend [4, S. 99ff]. α in [4] ist gleich dem hier verwendeten ε. Damit geht β in [4, Gl. (6.85)] über in:
| (26) | 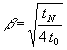 |
Wird die Oberfläche in [4] betrachtet, wird in [4, Gl. (6.85)]:
| (27) | ξ = 0 | da | x = 0 | an der Oberfläche |
Für den täglichen Temperaturgang (t0 ![]() 24 h) folgt aus (26) und (25) wegen der großen bzw. kleinen Werte von β, daß mit [4, (6.90) und (6.91)] die Oberfläche von Beton diesem Temperaturgang kaum folgt und dazu noch mit fast 6 h Zeitverzögerung, die Oberfläche von Dämmstoff folgt dagegen fast sofort. Längeren Bewegungen (Tagen, d.h. >> 60 h) folgen beide Oberflächen. In [1] wird nahelegt, jeder beliebigen Temperaturverlauf (Wärmestromverlauf) als geeignete Summe beliebig anderer Temperaturverläufe (Wärmestromverläufe) betrachtet werden kann. Die Linearität der Wärmedifferentialgleichung sorgt dafür, das jeder Einzelverlauf unabhängig von den anderen ist bzw. betrachtet werden kann.
24 h) folgt aus (26) und (25) wegen der großen bzw. kleinen Werte von β, daß mit [4, (6.90) und (6.91)] die Oberfläche von Beton diesem Temperaturgang kaum folgt und dazu noch mit fast 6 h Zeitverzögerung, die Oberfläche von Dämmstoff folgt dagegen fast sofort. Längeren Bewegungen (Tagen, d.h. >> 60 h) folgen beide Oberflächen. In [1] wird nahelegt, jeder beliebigen Temperaturverlauf (Wärmestromverlauf) als geeignete Summe beliebig anderer Temperaturverläufe (Wärmestromverläufe) betrachtet werden kann. Die Linearität der Wärmedifferentialgleichung sorgt dafür, das jeder Einzelverlauf unabhängig von den anderen ist bzw. betrachtet werden kann.
Welche Auswirkungen hat das nun? Die zeitweisen hohen Temperaturen der Dämmstoffoberfläche werden im allgemeinen die Oberfläche nicht beschädigen, dagegen können die tiefen Temperaturen wegen Tauwasserausfall zu einer Oberflächenbelastung führen. Fließt das Wasser ab und verdunstet nicht wieder, wird die beim Tauen freiwerdende Wärme weitgehend der Wand zugeführt. Die Oberflächen beider Stoffe folgen dem langfristigeren Temperaturgang, der von den Eigenschaften der Oberfläche und nicht vom Wandmaterial dahinter abhängt. Das gilt zunächst erst einmal die ∞ -dicke Wand, aber nach der Art der Herleitung ist anzunehmen, daß das auch für reale Wandstärken gilt. Das unterstreicht noch einmal die Aussagen in [2], daß der u-Wert bei allen Wandaufbauten gültig ist. Das der Einfluß der einzelnen Temperaturgänge unabhängig voneinander betrachtet werden kann, folgt aus der Linearität der Wärmeleitungsgleichung, wie in [2] gezeigt und auch in [4] angewandt wird.
Hinweisen möchte ich auch auf [9, S. 22 bis 37] wo ebenfalls die Wärmeleitungsgleichung mit Speicherung behandelt wird. Die in [9, S. 31] gemachte Bemerkung über die Vieldeutigkeit der Lösung bezieht sich auf ein mathematisch denkbares, aber real nicht realisierbares Phänomen (Wärmeexplosion). Außerdem könnte man das noch als kombinierte Anfangs- und Rand-Bedingungen sehen. Das bedeutet, daß in der Praxis die Lösung der Wärmeleitung mit Anfangs- und Rand-Bedingung eindeutig ist. Da die Anfangsbedingung bald abgeklungen ist folgt dann die Lösung eindeutig aus den Randbedingungen.
[1] Ebel, J.: Oberfläche und Speicherung. Word-Dokument in www.bauphysik.com vom 03.12.01
[2] Ebel, J.: Wie steht es mit der Gültigkeit des u-Wertes? Word-Dokument in www.bauphysik.com vom 12.11.01
[3] Stopp, F.: Operatorenrechnung. BSB B. G. Teubner Verlagsgesellschaft. Leipzig 1978
[4] Grigull, U.; Sandner, H.: Wärmeleitung. Springer-Verlag Berlin Heidelberg New York 1979
[5] Nehring, G.: Über den Wärmefluß durch Außenwände und Dächer in klimatisierte Räume infolge der periodischen Tagesgänge der bestimmenden meteorologischen Elemente. Gesundheits-Ingenieur 83 (1962) H. 7, S. 185 – 189; H. 8, S. 230 – 242; H. 9, S. 253 - 269
[6] Smirnow, W. L.: Lehrgang der höheren Mathematik Teil IV. VEB Deutscher Verlag der Wissenschaften. Berlin 1961
[7] Bronstein, I. N.; Semendjajew, K. A.: Taschenbuch der Mathematik. BSB B.G. Teubner Verlagsgesellschaft, Leipzig 1979
[8] Oberhettinger, F.; Badii, L.: Tables of Laplace Transforms. Springer-Verlag. Berlin Heidelberg New York 1973
[9] Doetsch, G.: Handbuch der Laplacetransformation Bd. III. Birkhäuser Verlag Basel und Stuttgart 1973
[10] Stefan 1879 - genaueres evtl. in [11]
[11] Boltzmann, L.: Ann. Phys. 22(1884) 31, 291 und 616
[12] Wien, W.: Ann. Phys. 58(1896) 662
[13] Jaworski, B.M. und Detlaf, A.A.: Physik griffbereit. Akademie-Verlag * Berlin 1973
[14] DIN EN ISO 9288: Wärmeschutz - Wärmeübertragung durch Strahlung - Physikalische Größen und Definitionen (ISO 9288:1989); Deutsche Fassung EN ISO 9288:1996. Ausgabe: 1996-08