Zuordnungen |
Gleichungen |
Tabellen |
in dieser Arbeit |
römische Zahlen |
römische Zahlen |
aus DIN 1052:2004-08 |
arabische Zahlen > 100 |
beginnend mit Buchstaben |
aus DIN 1052-2:1996-10 |
arabische Zahlen < 9 |
arabische Zahlen |
Tabelle I: Zuordnungen von Gleichungen und Tabellen von Arbeit und DIN's
Nach Veröffentlichung des Artikels zur Kippbelastbarkeit einer Dübelverbindung hat ein sehr fruchtbares Gespräch mit einem Fachkollegen statt gefunden. In Auswertung dieses Gesprächs ist der Artikel um die nachfolgenden Abschnitte Problemstellung und effektive Dübelanzahl (wirksame Dübelanzahl) erweitert worden.
In der Regel wird die Einspannung einer Stütze zweiachsig beansprucht (x- und y-Richtung). Zur Stabilitätsbetrachtung ist die Einspannung in den beiden zueinander senkrechten (orthogonalen) Achsen gemeinsam und/oder seperat zu untersuchen. Die Hauptbeanspruchung ist oft eine Kippbeanspruchung und die Befestigung erfolgt mit Dübeln. Dabei können in der einen Kippachse die Dübel ganz normal auf Zug bzw. Druck beansprucht werden (Normalfall der DIN 1052), während in der dazu senkrechten Achse die Dübelverbindungen auf Kippung beansprucht werden. Diese Beanspruchung ist Gegenstand der vorliegenden Untersuchung. Wegen der geringen zulässigen Momente ist auch ersichtlich, warum diese Kippbeanspruchung nie erfolgen sollte. Wahrscheinlich ist die Kippbeanspruchung deshalb auch nicht in die DIN 1052 aufgenommen: Diese Beanspruchung sollte für die statische Sicherheit nie eine Rolle spielen.
Dafür, daß diese Beanspruchung nie erfolgen darf, gibt es noch einen weiteren Grund. Verbindungen sind oft ein Schwachpunkt und deshalb dürfen Verbindungen nur als vorhanden angesetzt werden, wenn sie genormt sind. Für diese Beanspruchung der Verbindung gibt es aber keine Norm, d.h. diese Verbindung darf nicht angesetzt werden. Wenn aber keine Verbindung angesetzt wird, ist eine Stütze in dieser Achse als Pendelstütze zu behandeln.
Wenn man glaubt, daß die Verbindung als ganz starr anzusetzen ist (Kragstütze), so ist zu nachzuweisen, daß die Verformung unter den einwirkenden Kräften kleiner 1/1000 (DIN 1052 Teil 1 Punkt 10.2.5) der Länge ist. Ohne diesen Nachweis eine Stütze als Kragstütze anzunehmen ist ein Statikfehler.
Bei einem Moment in Richtung der Dübelachsen (also Kippung senkrecht zu den Dübelachsen) müssen mindestens zwei Dübelgruppen vorhanden sein. Das zulässige Moment für diese Beanspruchung erhält man als Produkt von zulässiger Zug- bzw. Druckkraft jeder Dübelgruppe (nach der DIN 1052) mal Abstand der beiden Dübelgruppen. Wenn jemand ein Moment für die dazu senkrechte Richtung (Moment also senkrecht zu den Dübelachsen) analog berechnet (zulässiger Zug- bzw. Druckkraft einer Dübelgruppe mal Dübellänge) und das so erhaltene Moment als zulässig bezeichnet, so begeht er einen großen Fehler, denn das zulässige Moment ist mindestens um den Faktor 6 kleiner, wie in der weiteren Arbeit beschrieben wird.
Die Fußpunkteinspannung einer Stütze wird auf Kippung beansprucht, wenn am Stützenkopf (bzw. längs der Stütze) eine Horizontalkraft (z.B. durch Wind) wirkt. Diese Horizontalkraft muß abgeleitet werden. Sind keine weiteren Ableitungen (z.B. eine Halterung am Stützenkopf) vorhanden, geschieht dies durch die Fußpunkteinspannung. Diese Ableitung ist nachzuweisen und bereitet in der Regel keine Probleme und wird daher in diesem Artikel nicht weiter betrachtet. Im Gegensatz zur relativ problemlosen Ableitung der H-Kraft ist die Ableitung des nachfolgend genannten Moments schwieriger. Dieses Moment entsteht, weil die H-Kraft und ihre Ableitung unterschiedlichen Angriffspunkte haben. Dieses Moment muß auch durch die Fußpunkteinspannung abgeleitet werden. Bei Holzkonstruktionen ist die Momentenbelastung einer Verbindung ungewöhnlich, da Holzkonstruktionen in der Regel ausgesteift werden. Dagegen kommen unausgesteifte Stahlkonstruktionen eher vor, aber auch bei diesen werden besser Aussteifungen angeordnet.
Ein zweites Beispiel ist ein Fahnenmast. Durch die Fahne wirkt am oberen Mastende eine Horizontalkraft. Die entstehenden Kräfte und Momente müssen wieder durch die Masteinspannung in den Erdboden abgeleitet werden. Wie ist die Masthalterung zu bemessen? Die Mastbemessung selbst ist ja kein Problem.
Die Betrachtung der Momentenableitung ist der Zweck des Artikels. Kann eine vorgegebene Konstruktion diese Aufgabe in allen normmäßigen Belastungen erfüllen oder nicht?
Bei der Zug-Druck-Belastung einer Verbindungskonstruktion ist bei einer Dübelgruppe die zulässige Belastung einer Dübelgruppe geringer als das Produkt von zulässiger Belastung des Einzeldübels mal Anzahl der Dübel. Diese Verringerung wird in der Norm als effektive Dübelzahl behandelt und durch Gleichung (210) in der DIN 1052:2004-08 behandelt. Wie ist nun die effektive Dübelanzahl bei Kippbeanspruchung?
Anmerkung 1: Ist die Fußpunkteinspannung nicht nur ein kurzes Stück Stahlblech, sondern eine lange biegesteife Einspannung, so wird das Moment nicht über die Dübel abgeleitet, sondern direkt an die Einspannung. Dieser Fall (oft bei Fahnenmasten zu finden) ist nicht Gegenstand der Untersuchung.
Anmerkung 2: Bei Fahnenmasten wirkt die Masteinspannung in der Regel als Köcher (bzw. Hülse), die Schrauben, die beide Köcherhälften zusammenhalten, haben nur die Aufgabe die beiden Hälften zusammenzuhalten. Damit der "Köcher" seine Aufgabe erfüllen kann, muß der Köcher genügend stabil sein. Deswegen sind das oft Doppel-T-Profile oder dicke Stahlbetonelemente. In der dazu senkrechten (orthogonalen) Richtung wirken die Schrauben, die die Köcherhälften zusammenhalten, als normale Bolzenverbindungen, die entsprechend der DIN 1052 berechnet werden können.
Anmerkung 3: Sind die Halterungen für die Bolzen zu weich, können die Halterungen nicht als Köcher wirken. Wird z.B. Flachstahl 10 mm x 100 mm und 60 cm Höhe in dem am Schluß gerechneten Beispiel verwendet, so würde sich unter Einwirkung der für die Dübelverbindung zulässigen Kräfte die Halterung um 19 cm verbiegen (gerechnet als Kragarm). Damit ist zu sehen, daß eine dünne Halterung keine Köcherwirkung hat. Die Köcherwirkung setzt erst ein, wenn dieHalterungsverbiegung kleiner als die Behinderung der Stützenkippung durch die Dübel ist. Gleichzeitig wird damit auch unterschieden, ab wann eine dicke oder dünne Einspannung vorliegt.
Anmerkung 4: Wenn die Einspannung als Köcher wirkt, ist natürlich die ausreichende Festigkeit des Köchers nachzuweisen.
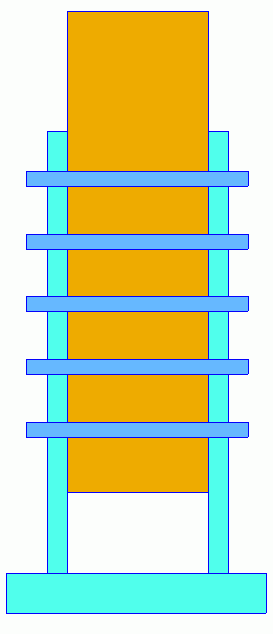
Betrachtet wird hier eine Fußpunkteinspannung mit mehreren Stabdübeln, die von Stahlblechen gehalten werden.

Bild I: Fußpunkteinspannung
Unter der Einwirkung eines Moments verformt sich die Einspannung, wie in den nachfolgenden Bildern II und III gezeigt ist. Die entstehenden Verformungsfiguren sind rot dargestellt. Bei der Verformung entstehen zwei Extremfälle, wobei immer die Längenänderungen der Stahlbleche klein gegenüber den Holzverformungen sind, so daß die Längenänderungen der Stahlbleche vernachlässigt werden können:
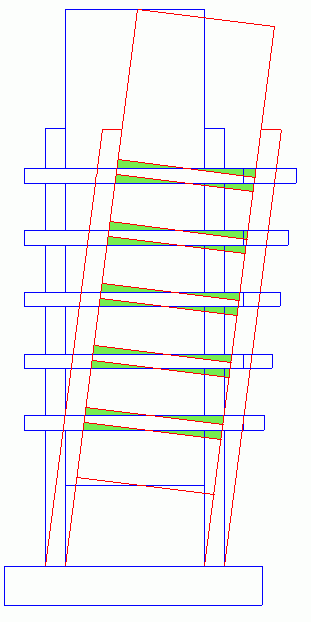
1. Sind die Stahlbleche dünn, dann werden die vertikalen Stahlbleche der Kippbewegung der Stütze folgen. Der Drehpunkt der Kippbewegung liegt dabei etwa in Höhe der Stahlblechbefestigung. Dabei bleiben die Verbindungspunkte Dübel / Stahlblech auf gleicher Höhe und alle Dübelverbindungen haben prinzipiell die gleichen Verformungen. Das Gesamtmoment bei gegebener Verformung ergibt sich dann als Produkt von Einzelmoment mal effektive Dübelanzahl (die geringer ist als die tatsächliche Dübelanzahl). Anders ausgedrückt: das Produkt von Einzeldübelbelastung mal Dübelanzahl muß abgemindert werden mit dem Verhältnis effektive Dübelanzahl zur tatsächliche Dübelanzahl. Dieser Typ Verformung ist in Bild II dargestellt.
2. Der Drehpunkt liegt in der Mitte der Dübelgruppe. Das Holz wird bei jedem Dübel in Abhängigkeit seiner Entfernung vom Drehzentrum anders verformt (nähere Abstände weniger). Der Beitrag jedes Dübels zum Gesamtmoment hängt von seiner Entfernung vom Drehzentrum ab, so daß die am weitesten entfernten Dübel den größten Beitrag liefern, nähere weniger. Die näheren Dübel verformen das Holz weniger. Dieser Typ Verformung ist in Bild III dargestellt.
 |
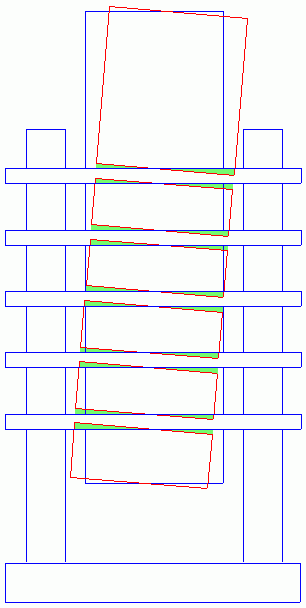 |
| Bild II: Verformung bei dünnen Stahlblechen | Bild III: andere Verformung |
Die Verformungen des Holzes sind die Differenzen zwischen der Ruhelage und der verformten Lage. In den Bildern II und III ist diese Verformung grün dargestellt.
Bei allen Beanspruchungen wird die zulässige Beanspruchung durch die maximal zulässigen Holzverformungen begrenzt. Bei Verformungen Bild II treten die maximalen Verformungen an allen Scherflächen auf. Bei Verformungen Bild III treten die maximalen Verformungen nur an den Scherflächen der äußersten Dübel auf.
Noch eine Anmerkung: Oft steht eine Stütze auf einer Platte der Fußpunkteinspannung. Prinzipiell trägt auch diese "Verbindung" zur Festigkeit der Verbindung bei - aber der Beitrag ist so unerheblich, daß er außer Berücksichtigung bleiben kann. In den seltensten Fällen wird ein paßgenaue Verbindung sein, die etwas dazu beitragen könnte.
Bei der Verformung Bild II reicht die Untersuchung einer Dübelverbindung. Auch bei der Verformungung nach Bild III kann das Gesamtmoment auf die einzelne Dübelverbindung zurückgeführt werden. Das geschieht nachfolgend:
Betrachtet wird eine einzelne Dübelverbindung. Es wird hier nur betrachtet, das der Dübel sich nicht verformt. Die Holzverformung (grün) ist die Differenz zwischen der schwarzen Ruhelage und der roten verformten Lage - zunächst nur bei Drehung im Dübelmittelpunkt (Bild IV) und dann bei Drehung um das Drehzentrum mit dem Abstand e zwischen Drehzentrum und Dübelmittelpunkt.
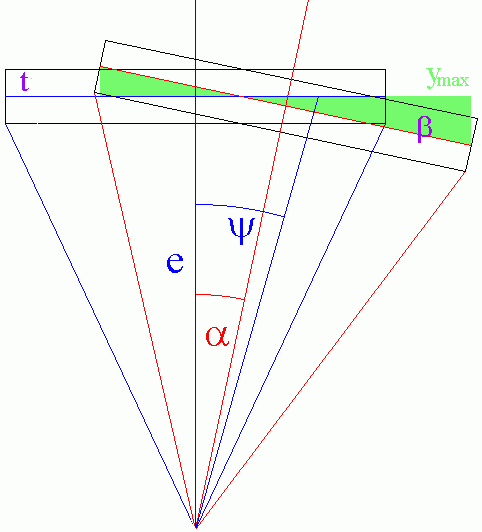
Bild IV: Verformung bei Abstand zwischen Drehzentrum und Dübel
In der Regel gibt die maximale Holzverformung ymax die Grenze der Belastbarkeit vor. Liegt der Drehpunkt im Dübelmittelpunkt und wird der Dübel bis zu dieser Holzverformung gedreht, so wird der maximale Drehwinkel erreicht:
![]()
oder
![]()
Betrachtet werden lineare Zusammenhänge zwischen Holzverformung und auftretender Kraft. Mit einer (hier nicht weiter untersuchten Konstante K) wird das Moment bei einer Drehung um einen Winkel β (x ist die Koordinate in Dübelrichtung - Nullpunkt beim Drehpunkt, y senkrecht dazu die Verformungsrichtung:
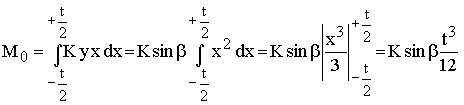
Die nachfolgende Betrachtung wird vereinfacht, wenn mit Winkelfunktionen gearbeitet wird. Dazu wird folgende Substitution (mit einer beliebigen Länge e) vereinbart:
![]()
Nach den Regeln der Integrationsrechnung wird damit
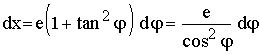 und
und 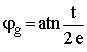
Eingesetzt wird damit:
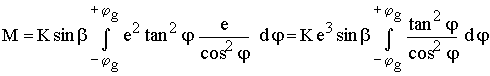
Das Integral wird nicht weiter gelöst, da der Wert schon berechnet ist.
Nun ist das Moment zu bestimmen, wenn sich die Stütze um ein Drehzentrum dreht. Die Definition des Momentes bleibt natürlich unverändert. Substituiert wird hier ein Winkel ψ statt φ. Damit wird (e ist hier der Abstand zwischen dem Drehzentrum und dem Dübelmittelpunkt):
![]()
Nun sind x und y (Holzverformung) in Abhängigkeit von ψ zu bestimmen. ψ bestimmt einen Punkt auf der Ruheachse des Dübels und die Entfernung vom Drehpunkt. Die y-Koordinate ist unabhängig vom Winkel und immer e. Für die x-Koordinate gilt:
![]()
Für die Abstand l* gilt:
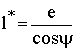
Ein Punkt der verdrehten Achse hat andere Koordinaten. Bestimmt wird der Schnittpunkt der Verbindungsgerade Drehpunkt mit betrachteter Punkt auf der Ruhelage der Dübelachse mit der verformten Dübelachse. Der Winkel zwischen dem verdrehten Dübelmittelpunkt und dieser Verbindungsgerade soll φ heißen. Zwischen einem Drehwinkel α des Dübels und den Winkeln ψ und φ besteht dann folgende Beziehung:
ψ = α + φ
Für die Länge l zwischen Schnittpunkt und Drehpunkt besteht folgende Beziehung:
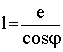
Durch die Strahlungsgleichungen ergeben sich folgende Koordinaten des Schnittpunkts:
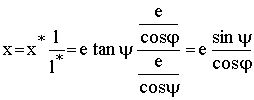
Analog ergibt sich die y-Koordinate yk:
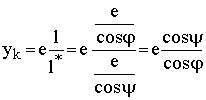
Die Holzverformung ergibt sich als Differenz der y-Koordinaten von unverdrehten und verdrehten Holz:
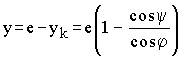
Die Werte können nun eingesetzt werden, wodurch sich ergibt:
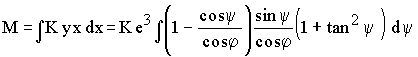
Nun wird noch ψ durch φ ausgedrückt:
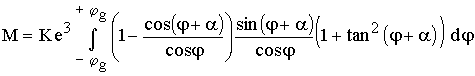
Mit den Additionstheoremen wird:
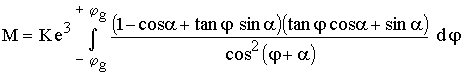
Der Nenner ist noch anders zu untersuchen:

Unter der Voraussetzung, daß tan φ tan α < 1 ist (d.h. die maximale Auslenkung ist kleiner als der Abstand - siehe spätere Anmerkung), kann der Nenner in eine geometrische Reihe entwickelt werden:
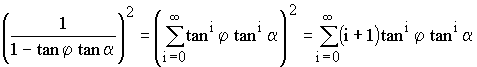
In der Praxis ist tan φ tan α << 1, so daß die Reihe schnell konvergiert. Damit lautet das Integral:
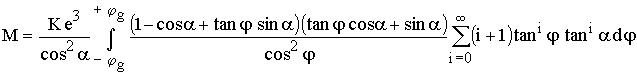
Anmerkung: Wird e so klein, daß die Reihenentwicklung nicht mehr zulässig ist, so ist der Unterschied zwischen M (bei e > 0) und M0 (bei e = 0) so gering, daß mit M0 gerechnet werden darf.
Nun wird rückgängig substituiert:
![]()
Nach den Regeln der Integrationsrechnung wird damit
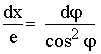 und
und 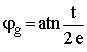
Damit lautet das Integral:
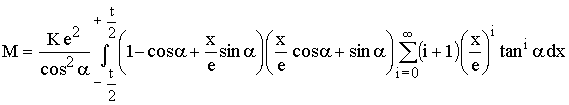
Nach Umsortieren (und extra Darstellung des Klammerausdrucks [Kla]) wird:
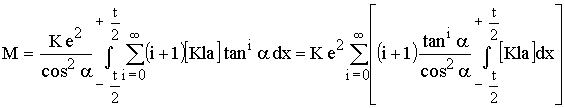
Mit dem Klammerausdruck:
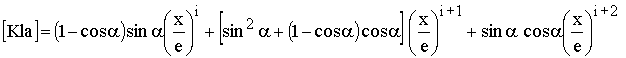
Die Integration kann jetzt ausgeführt werden:
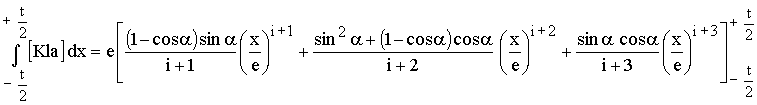
Beiträge zum Integral liefern nur Terme, bei denen der Exponent von x ungerade ist. Terme mit geraden Exponenten addieren sich zu Null. Damit wird mit i = 2j bzw. i = 2j +1:
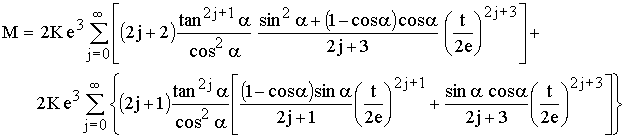
Nun wird noch ein Teil der t-Potenzen herausgezogen:
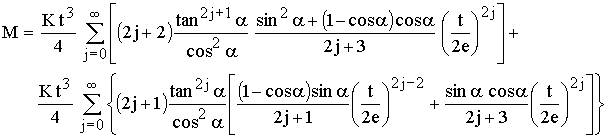
Als maximale Holzverformung ergibt sich:
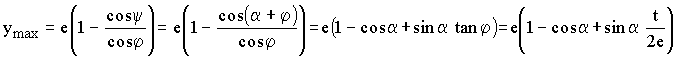
Oder ausmultipliziert:

Wegen des Zusatzterms sind bei gegebener maximaler Verformung nur kleinere Winkel α zulässig und gewollt. Die Gleichung zeigt: je größer e ist, um so kleiner ist α. Für alle e > 0 ist bei gleicher Verformung der zulässige Winkel α immer kleiner als der Winkel β.
Anmerkung: Diese Verkleinerung des Verformungswinkels, die die störende Verformung unter Belastung verringert, ist zugleich die Ursache einer geringeren zulässigen Belastung.
Weitere Anmerkung: Aus vorstehender Gleichung folgt die weiter oben genannte Voraussetzung, daß ymax < e sein muß. Zuerst wird die Gleichung durch e dividiert:
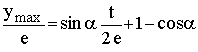
Nach Vereinbarung ist t/(2e) gleich tan φg. Damit wird:
![]()
Umgestellt wird daraus:
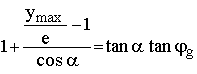
Solange ymax < e ist, ist der rechte Term auf der linken Seite immer negativ, so daß die linke Seite immer kleiner 1 ist.
Wenn der Dübel durch das Drehzentrum geht, ist die Formel für M nicht zutreffend, da dann die maximale Auslenkung nicht kleiner als der Abstand ist, was die Voraussetzung für die Herleitung war. Dann ist die schon oben abgeleitete Formel zu verwenden:
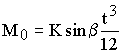
Durch den Abstand des Dübels vom Drehzentrum ergibt sich ein anderes Moment als wenn der Dübel durch das Drehzentrum geht. Damit wird für das Verhältnis:
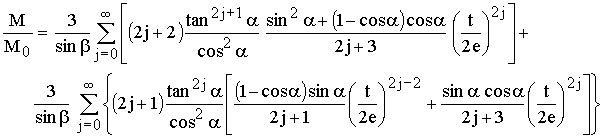
Umgeformt wird daraus:
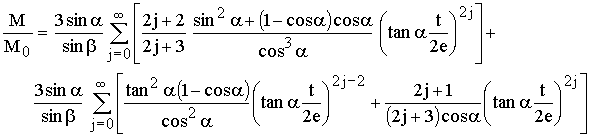
Da der Winkel α immer kleiner als der Winkel β ist und die Abstände ei der Dübel i bei verschiedenen Dübeln unterschiedlich sind, ist der Beitrag des einzelnen Dübels zum Gesamtmoment unterschiedlich. Bezieht man das Gesamtmoment aller Dübel auf das maximal zulässige Moment eines Einzeldübels, so kann man diesen Quotienten als effektive Dübelanzahl nd bezeichnen. Mit der vorstehenden Gleichung wird also die effektive Dübelanzahl:
![]()

Die effektive Dübelanzahl nd ist unter der Annahme berechnet, daß jede einzelne Holzverformung keine Auswirkung auf eine andere Holzverformung hat. Diese Annahme ist nicht zutreffend, so daß die effektive Dübelanzahl weiter zu reduzieren ist:
Diese weitere Reduktion hat die gleichen Ursachen wie bei der Zug-Druck-Beanspruchung: Eine Holzverformung unter der Einwirkung eines Dübels beschränkt sich ja nicht nur auf die unmittelbare Umgebung des Dübels, sondern breitet sich weiter im Holz aus. Ein anderer Dübel, der sich im Verformungsbereich dieses Dübels befindet, wird die maximal zulässige Holzverformung schon bei geringerer Belastung erreichen als ohne diese Vorverformung. Dieser Effekt wird durch die effektive Dübelanzahl nef der Gleichung (210) in der DIN 1052:2004-08 berücksichtigt.
Da die Effekte nd und nef unabhängig voneinander sind und gleichzeitig wirken, müssen beide Abminderungsfaktoren multiplikativ behandelt werden.
Da es im Einzelfall von vielen Faktoren abhängt, ob eine Verformung nach Bild II oder Bild III (oder irgendein Übergang dazwischen) eintritt, ist aus Sicherheitsgründen die maximal zulässige Belastung nach der Verformung nach Bild III zu berücksichtigen, die zu nd geführt hat. Ist im weiteren die Verformung zu berücksichtigen, ist als mögliche Verformung die Verformung nach Bild II zu berücksichtigen und nicht die geringere Verformung nach Bild III, weil die Verformung ebenfalls im Einzelfall von vielen Faktoren abhängt.
Ist der Abstand (bei Verformungen nach Bild III unvermeidlich) zwischen dem Holz und dem Stahlblech sehr groß, so verformt sich der Dübel selbst schon außerhalb des Holzes, so daß die Holzverformung geringer ausfällt. Dadurch werden geringere Kräfte vom Dübel auf die Stütze übertragen, so daß die effektive Dübelanzahl weiter zu verringern ist. Diese Verringerung kann bis zu 0,5 betragen.
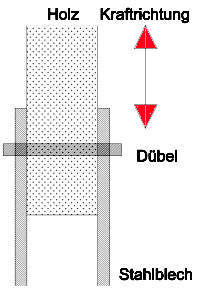 |
 |
| DIN 1052 | ungenormt (andere Kraftrichtung beachten) |
Kraftrichtungen nach DIN 1052 und in dieser Arbeit
Eigentlich sollte die Kippfestigkeit (Kippsicherheit) einer Dübelverbindung nicht interessieren, denn sie sollte unwesentlich für den Nachweis der Stabilität einer Konstruktion sein. Zitat aus einem Skript des Holzbauinstituts der TU München http://www.fgh.bv.tum.de/Daten/Skript/WS0506%20-%20Kapitel%208.pdf : "Skelettsysteme sind wie Kartenhäuser: Sie müssen ausgesteift werden."
Oder Punkt 8.8.1 (9) der DIN 1052:2004-08: "... die Drehsteifigkeiten aller Anschlüsse berücksichtigt werden ...". Punkt 8.8.3 (6) der DIN 1052:2004-08: "... Stöße dürfen als drehstarr angenommen werden, wenn ... bei dem 3-fachen Bemessungswert der Momente ..."
Wenn eine Konstruktion ausgesteift ist, werden die einzelnen Verbindungen nicht auf Kippung beansprucht, sondern auf Zug, Druck und Abscheren. Wegen der Unzweckmäßigkeit der Beanspruchung auf Kippung existieren auch keine Vorschriften zur Ermittlung der Kippfestigkeit.
Auch kein Hersteller von Statiksoftware unterstützt die Berechnung dieser Kippfestigkeit, weil kein verantwortungsbewußter Statiker ein Kartenhaus berechnet.
Wenn aus irgendwelchen Gründen eine Konstruktion trotzdem nicht ausgesteift ist oder ausgesteift werden kann, kommt es doch vor, das Verbindungen auf Kippung beansprucht werden. Während bei der Beanspruchung auf Zug bzw. Druck die Verformungen fast nie eine Rolle spielen (die Nachweise auf Ausknicken usw. sind natürlich erforderlich), ist die Verformung bei der Beanspruchung auf Kippung in der Regel wesentlich. Bei Stützen erhöht die Nachgiebigkeit der Verbindung die Kipplänge in der Regel dramatisch (siehe z.B. Heimeshoff, B.: Bemessung von Holzstützen mit nachgiebigen Fußanschluß. Holzbau-Statik-aktuell, Folge 3 Mai 1979, ISSN 0720-9568) - auch wieder im Gegensatz dazu, wenn das Kippen auseinanderliegende Dübel belastet, wobei jeder einzelne Dübel (jede einzelne Dübelreihe) nur auf Zug bzw. Druck mit der entsprechenden Nachgiebigkeit belastet wird. Das der Dübel auch auf Abscheren belastet wird, spielt im vorliegenden Zusammenhang keine Rolle.
Nachfolgend wird genannt mit welchen Festigkeiten gerechnet werden kann. Anschließend wird hergeleitet, wie diese Formeln entstehen. Betrachtet werden zweischnittige Dübelverbindungen.
Die Gleichungen alte und neue DIN liefern ähnliche Werte - aber z.T. Abweichungen bis 50 % (siehe Beispiele am Schluß). Dabei ist auch zu berücksichtigen, daß die neue DIN hauptsächlich die Kraftangaben an einer Scherfuge liefert, während die alte DIN die Gesamtkraft des Dübels angibt, d.h. für 2 Scherfugen. Daraus folgt, daß in Gleichungen für das Moment usw., die Nst,b enthalten (entsprechend der alten DIN) Nst, b durch 2 Rk zu ersetzen ist.
Anmerkung: Die Gleichung (199) der DIN 1052: 2004-08 entspricht der Gleichung (4) der DIN 1052-2: 1996-10 - fast nur mit dem Unterschied, daß der Exponent nicht 2, sondern ca. 1,8 ist. Durch den Absatz 12.2.3 (7) wird Gl. (199) so modifiziert, daß daraus die Gleichung (3) wird - wobei der Exponent der modifizierten Gleichung (199) fast 1 ist, im Unterschied zu Gl. (3), wo er genau 1 ist.
Bei Ungleichungsketten ist der linke Wert der Grenzwert für kurze Dübel, der rechte Wert der Grenzwert für lange Dübel.
![]()
![]()

Wird in die Gleichung für die Drehfeder noch das zulässige Moment eingesetzt, wird die Abhängigkeit von der Dübellänge deutlich (mit der dritten Potenz, da auch noch Nst,b von a abhängig ist.). Werden die Abminderung oder/und die Längenabhängigkeit nicht berücksichtigt, kann das ggf. dramatische Auswirkungen haben.
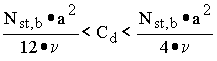 oder
oder ![]()

Darin bedeuten entsprechend der DIN mit Ergänzungen:
zul Nst,b: zulässige Belastung nach Abschnitt 5 der DIN 1052-2: 1996-10
zul Mst,b: zulässiges Belastungsmoment (zusätzlich definiert)
ν: Verschiebung bei zul Nst,b nach Tabelle 13 der DIN 1052-2: 1996-10
C: Verschiebungsmodul nach Tabelle 13 der DIN 1052-2: 1996-10
Cd: Drehsteifigkeit (zusätzlich definiert - analog Literatur Heimeshoff)
a: Holzdicke nach Abschnitt 5.8 der DIN 1052-2: 1996-10 = Dübellänge
dst,b: Durchmesser des Dübels nach Abschnitt 5.8 der DIN 1052-2: 1996-10
Außer dem zulässigem Moment zul Mst,b ist bei Kippung unbedingt die Verformung und die Vergrößerung der Knicklänge zu beachten.
Da keine Normen zur Bemessung der Kippung für Verbindungsmittel existieren, sind vorhandene Normen sachlich auch auf den Fall der Kippung von Verbindungsmitteln anzuwenden.
Was sind diese Ausgangspunkte?:
Diese Annahmen liefern genügend Voraussetzungen um die Kippung nachzuweisen. Aber sie zeigen auch Unterschiede:
Der Proportionalitätsfaktor zwischen Teilkraft und Verformung ist nicht ganz proportional der verformten Fläche. Sonst wäre z.B. keine Abminderung wie in Gleichung (203) der DIN 1052:2004-08 notwendig. Das ist erklärlich: Wird durch den Dübel das Holz gedrückt, so wird nicht nur das Holz direkt unter dem Dübel verformt, sondern auch das Holz seitlich davon. Es entsteht eine Verformungsmulde, die viel breiter als der Dübel ist. Dadurch ist bei gleicher maximaler Holzverformung wegen dieser seitlichen Ausbreitung die spezifische Kraft bei dickeren Dübeln kleiner (bzw. bei gleicher spezifischer Kraft die Mulde tiefer).
Zum leichteren Verständnis der Kippbelastbarkeit werden zunächst die Verhältnisse bei Zug und Druck betrachtet.
Mit den oben genannten Voraussetzungen ist eine Differentialgleichung für die Dübel- und Holzverformung aufzustellen und zu lösen. In die Lösung geht die Art der Dübelhalterung ein. Sind die haltenden Stahlbleche dünn, so ist die Verbindung Halterung/Dübel relativ "lose", da sich der Dübel mit seiner Achsenrichtung in der Halterung drehen kann, bzw. das Blech einer Dübelbewegung folgt. Ist das haltende Stahlblech dick, so wird der Dübel in der Halterung in seiner Ausgangsrichtung "fest" gehalten und die Richtung der Dübelachse kann sich nicht drehen.
In der neuen DIN 1052 wird deshalb zwischen dünn und dick (bzw. lose und fest) unterschieden. Die Lösungen für die zweischnittigen Verbindungen lauten (die Proportionalitätskonstante bei Zug bzw. Druck und Proportionalitätskonstante mal Dübellänge sind noch hinzuzufügen - die verwendeten Winkelfunktionen sind abgekürzt dargestellt):
C: coshyp(x)
S: sinhyp(x)
c: cos(x)
s: sin(x)
| lose | fest | ||
| Zug (Druck) | 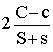 |
Bild V | |
| Kippung | 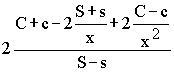 |
Bild VI | |
| Abminderungsfaktor AF | Bild VII |
Tabelle II
In Bild V und Bild VI sind diese Funktionen für gleiche maximale Holzverformung dargestellt - als Funktion der relativen Länge. Bezugslänge ist die Hälfte von treq bei fester Halterung. In Bild V sind außerdem noch die Grenzwerte der Belastbarkeit nach Gleichung (197) bzw. (199) der DIN 1052: 2004-08 eingetragen - einschließlich der Forderung 12.2.3(6). Der Knickpunkt der Grenzkurve (Übergang vom linear ansteigenden Teil auf den konstanten Wert) sind die Mindestholzdicken treq.
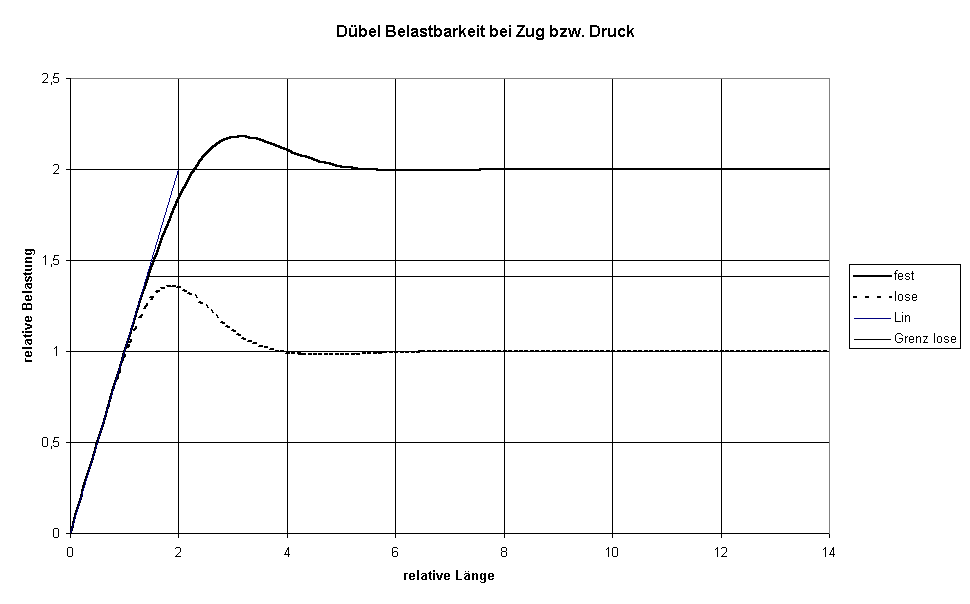
Bild V: Zug- (Druck-)kraft in Abhängigkeit von der Dübellänge bei gleicher maximaler Verformung
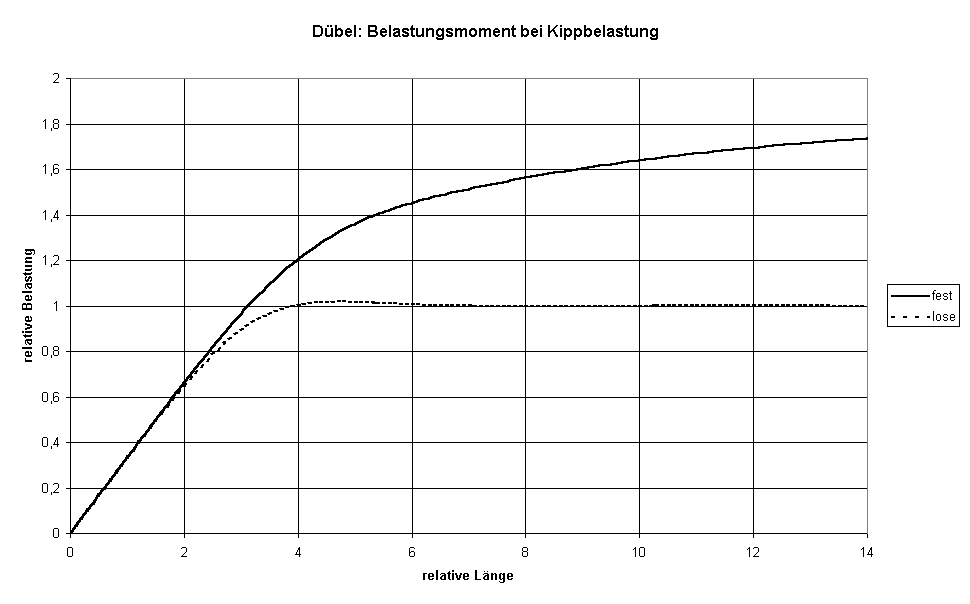
Bild VI: Kippmoment in Abhängigkeit von der Dübellänge bei gleicher maximaler Verformung
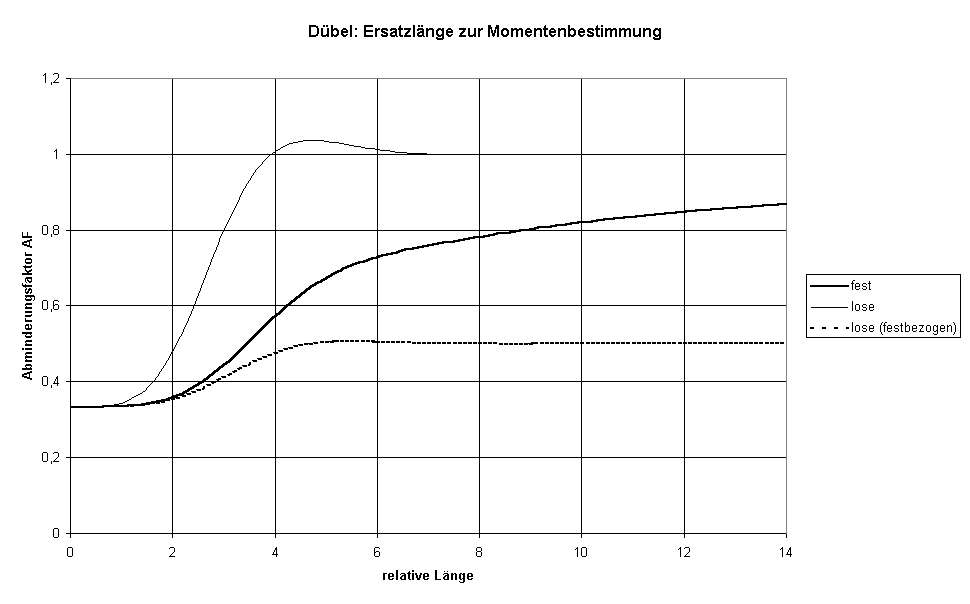
Bild VII: Quotient von Kippmoment und Zugkraft in Abhängigkeit von der Dübellänge bei gleicher maximaler Verformung
In der alten DIN 1052-2 Gleichungen (3) und (4) ist nur die "feste" Kurve verwandt. Der Übergang von Gleichung (3) auf (4) erfolgt bei einer bestimmten Holzdicke areq, die die gleiche Bedeutung wie treq der neuen DIN hat. Für areq gilt mit den Bezeichnungen der alten DIN:
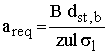
Die Holzverformung längs des Dübels ist in Bild IIX dargestellt. Bei langen Dübeln ist die Verformung praktisch nur im Randbereich vorhanden. Diese Randverformung als Auszug aus Bild IIX ist in Bild IX dargestellt. Bei kurzen Dübeln spielt die Abnahme der Holzverformung (durch Zunahme der Dübelverformung) noch keine Rolle - deswegen nimmt die Belastbarkeit mit der Dübellänge zu, bei langen Dübeln verformt sich der Dübel im Mittelbereich so, daß der Dübel der Holzbewegung folgt. Damit entsteht keine Holzverformung und damit wirken in diesem Bereich des Dübels auch keine Kräfte auf das Holz.
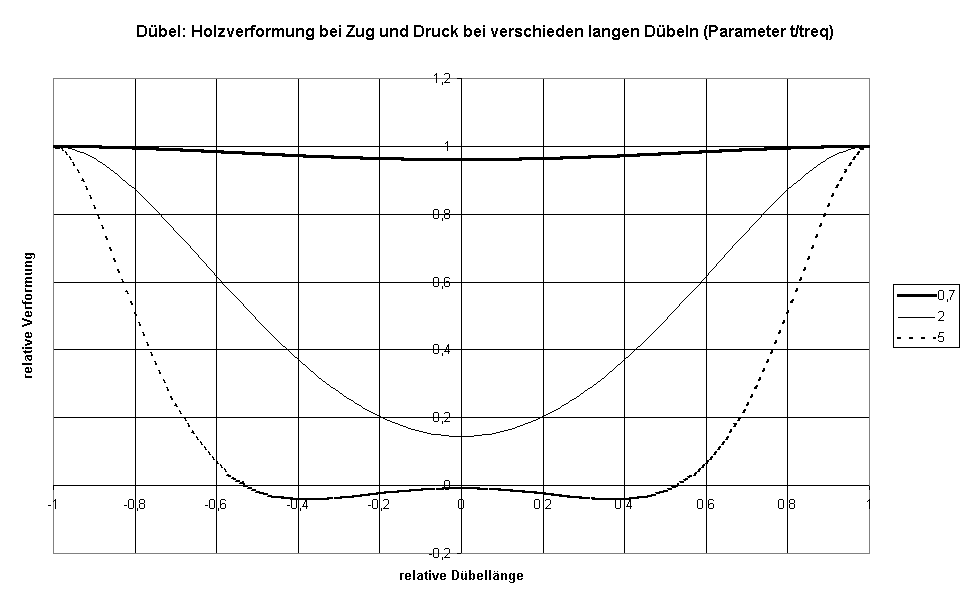
Bild IIX: Holzverformung infolge Zug (Druck) bei Dübeln in Abhängigkeit der Gesamtlänge
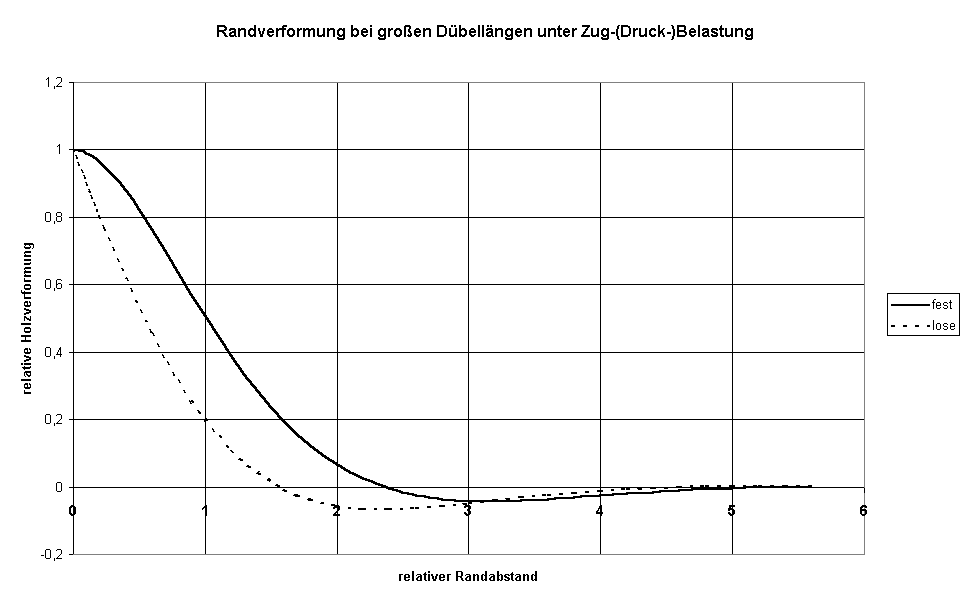
Bild IX: Holzverformung infolge Zug (Druck) bei langen Dübeln im Randbereich
Die Grenze der Belastung bei großer Dübellänge und loser Halterung ist größer als die Hälfte der Belastungsgrenze bei fester Halterung (das wäre der Wert "1") und hat nach der Norm den Wert "Wurzel(2)". Obwohl Bild V den Wert "1" nahe legt ist der größere Wert trotzdem richtig. Es geht um den Versagensmechanismus und da spielen negative Holzverformungen keine Rolle - siehe Bild IX, daß die Holzverformungen (und nur diese sind für die Kraftwirkungen verantwortlich) im Randbereich zeigt. Die Holzverformungen sind bei loser Halterung wesentlich geringer und haben noch dazu größere negative Anteile.
Die Belastungsgrenze einer Dübelverbindung wird also durch die maximal zulässige Holzverformung bestimmt und es ist unerheblich, wie diese zu Stande kommt. In der alten DIN (Tabelle 13) wurde die maximale Holzverformung unabhängig von der Dübeldicke angegeben. In der neuen DIN (Tabelle G.1) ist sie von der Dübeldicke abhängig - und zwar etwa mit d0,3. Der Exponent ergibt sich aus dem Quotienten von Tabelle G.1 (1,5) und der Abhängigkeit von Rk mit etwa 1,8.
In den Formeln der Tabelle II sind schon die Faktoren bei Kippbelastung gezeigt. Die Holzverformung bei verschieden langen Dübeln unter Kippbelastung zeigt Bild X. Bei kurzen Dübeln ist die Holzverformung linear und konzentriert sich mit zunehmender Dübellänge immer mehr an den beiden Dübelenden. Bei langen Dübeln ist der Verlauf der Randverformung als Auszug aus Bild X in Bild XI dargestellt. Dieser Verlauf ist fast der gleiche wie bei Zug-Belastung. Anmerkung: Bei Zugbelastung liegt an beiden Dübelenden die gleiche Zug- bzw. Druckbelastung vor, so daß die Gesamtbelastbarkeit = 2 Rk (DIN 1052: 2004-08) ist, bzw. gleich Nst,b (DIN 1052-2: 1996-10). Unter dieser Voraussetzung (sehr langer Dübel) ist das zulässige Belastungsmoment direkt aus der Momentendefinition (Kräftepaar mal Abstand des Kräftepaares) zu bestimmen.
zul M = Rk × t
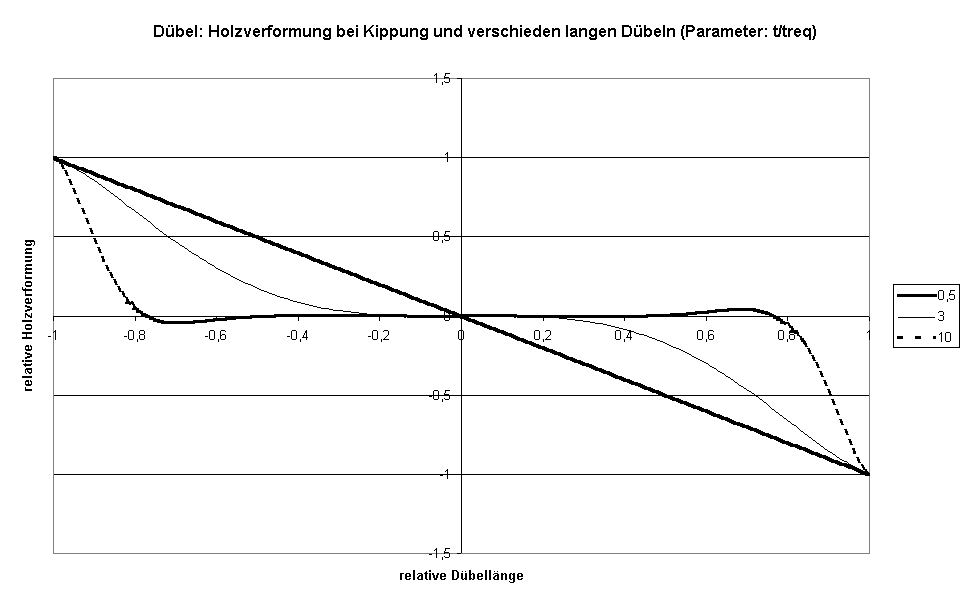
Bild X: Holzverformung infolge Kippung bei Dübeln in Abhängigkeit der Gesamtlänge
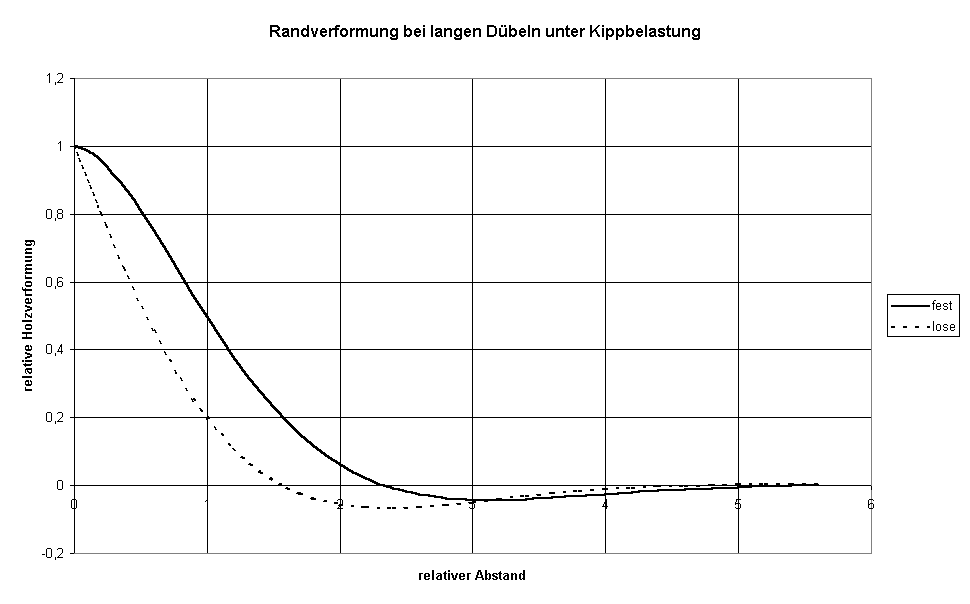
Bild XI: Holzverformung infolge Kippung bei langen Dübeln im Randbereich
Bei kürzeren Dübeln wird mit dieser Gleichung die Momentenberechnung falsch, da kein Kräftepaar vorliegt, sondern näherungsweise eine dreieckförmige Streckenlast - je kürzer der Dübel um so dreickförmiger. Für eine derartige dreieckförmige Streckenlast können haben die Kräfte, die der Dübel auf die Halterung ausübt, nicht den gleichen Wert wie die Kräfte bei Zugbelastung - trotz gleicher maximaler Holzverformung, weil die Holzverformung und die Kräfte des Holzes auf den Dübel ganz andere sind. Die Kräfte sind erheblich geringer - bei kurzen Dübeln nur 1/3. Den Verlauf dieses Abminderungsfaktors AF zeigt Bild VII, die Werte ergeben sich als Quotient der Faktoren von Zug und Kippung in Tabelle II. Der Wert AF beginnt bei kurzen Dübeln mit 1/3 und hat als Endwert 1 (oder 0,5 bei "losen" Dübeln) bei langen Dübeln.
Die Drehsteifigkeit Cd der Verbindungen ergibt sich als Quotient von Belastungsmoment und dem sich dabei einstellendem Winkel. Bei kleinen Drehwinkeln ist der Tangens des Bogenwinkels fast gleich der Bogenlänge. Da sich die Verbindung um den Längsmittelpunkt des Dübels dreht, ist der Winkel gleich Randverschiebung durch halbe Dübellänge.
![]()
Für M und φ sind immer zusammengehörige Werte zu betrachten. Wenn M mit Punkt 12.3 (8) (Gleichung (209)) erhöht wird, erhöht sich auch φ in dem gleichen Maße, d.h. die Drehsteifigkeit ist unabhängig bei welcher Belastung sie bestimmt wird - solange der Linearitätsbereich nicht verlassen wird. Entsprechend der Belastungskurve der Nachgiebigkeit wird die Steifigkeit geringer, wenn die Belastung den Linearitätsbereich überschreitet.

Mit Einsetzen der Werte ergibt sich aus der neuen DIN mit Kser aus Tabelle G.1:
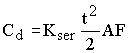
Wenn der Fußpunkt nachgiebig angeschlossen ist, ergibt sich eine Vergrößerung der Knicklänge sk der Stütze mit der Höhe h.
Mit Heimeshoff ergibt sich:
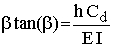
Nach Lösung der Gleichung kann mit β die Knicklänge bestimmt werden:
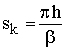
Bei einer Kragstütze ist Cd = ∞ und dementsprechend β = π /2 und deswegen sk = 2 h.
Wenn die Stütze unter Belastung etwas kippt, wird sich der Stützenkopf verschieben. Die Verschiebung ergibt sich:
Stützenkopfverschiebung = h φ
Beim kurzen Dübel ist die Holzverformung fast exakt dreieckförmig (Bild IX) und so kann die maximal zulässige Belastung ohne Differentialgleichung berechnet werden. Integrationen sind aber erforderlich.
Warum ist der Schluß maximal zulässiges Moment gleich maximal zulässige Kraft mal Dübellänge unzulässig? Um das deutlich zu machen, werden zunächst die elastischen Verhältnisse bei Zug- und Druckbeanspannung erläutert, die zu den Gleichungen (3) und (4) der DIN 1052-2 führen.
Die auf das Holz der Stütze übertragenen Kräfte verformen das Holz. Im linearen Bereich der Verformung ist Kraft und Verformung proportional. Bei einer Zug- (Druck)belastung ist bei kurzen Dübeln die Holzverformung auf der gesamten Dübellänge konstant und deshalb ist auch jede Teilkraft längs eines Dübelabschnitts gleich, so daß die Gesamtkraft als Summe aller Teilkräfte proportional der Dübellänge a ist [Gleichung (3)]. Formelmäßig ist die Kraft N mit einer Federkonstante K und der Verschiebung ν folgendermaßen darzustellen(mit Rücksicht auf die spätere Momentenberechnung werden linke und rechte Dübelhälfte extra genannt):
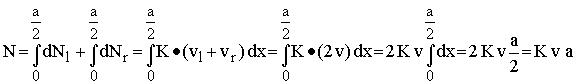
Bei größeren Dübellängen verformt sich durch die Kräfte auch der Dübel selbst in Richtung der Belastung, so daß die Holzverformung geringer wird und damit ist im Bereich der Verformung des Dübels die Kraftwirkung auf das Holz (und damit die Holzverformung) geringer und wird schließlich zu Null. Nur im Randbereich wird allein das Holz (und nicht der Dübel) verformt. Dadurch trägt nur der Randbereich zur zulässigen Belastung bei und die zulässige Belastung wird unabhängig von der Dübellänge (sofern der Dübel ausreichend lang ist!). Die Größe dieses Randbereiches hängt vom Dübeldurchmesser dst,b ab und damit wird die zulässige Belastung durch Gleichung (4) der DIN 1052-2 richtig beschrieben. Löst man die entstehende Verformung des Dübels als Dgl. und bestimmt damit die maximal zulässige Belastung der Dübelverbindung als Funktion der Dübellänge, so erhält man eine geschlossene Lösung (mit Hyperbelfunktionen), die als Grenzfälle für kurze (bzw. lange) Dübel die Gleichungen (3) bzw. (4) als Grenzfälle enthält und im Übergangsbereich von kurzen auf lange Dübel nur eine Abweichung von ca. 8 % zu den Gleichungen (3) und (4) hat.
Nach dieser Vorbemerkung nun die maximal zulässige Momentenbelastung eines Dübels. Bei der Kippung ist die Holzverformung längs des Dübels nicht konstant und ändert sich bei kurzen Dübeln von Stauchung auf der einen Seite über Null in der Mitte auf Dehnung auf der anderen Seite linear (Bild IX). Dabei ist die Holzverformung am Rand am Größten - aber darf auch dort nicht die maximal zulässige Holzverformung überschreiten. Da bei Überschreitung der zulässigen Holzverformung das Holz zerstört wird, ist der Maximalwert der Holzverformung bei Zugbelastung (Druckbelastung) und Kippung gleich. Damit ist für die Holzverformung anzusetzen:
![]()
Nun ist für jeweils 2 Teilabschnitte links und rechts in gleicher Entfernung von der Mitte das entsprechende Teilmoment des Kräftepaares (= Kraft mal Abstand) zu bestimmen:
![]()
Alle Teilmomente zum Gesamtmoment zu integrieren (eine weitere 2 tritt nicht auf, da beim Kräftepaar schon linke und rechte Hälfte berücksichtigt sind):
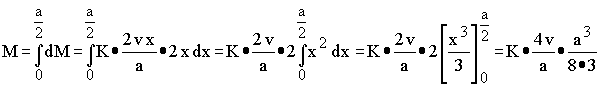
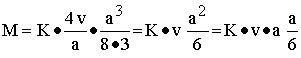
Aus dem Vergleich mit N = K v a folgt:
![]()
Aus dem Beispiel sieht man, daß die Interpretation des Produktes von zul N * Dübellänge als zul M unzulässig ist.
| Eingabe der Werte | ||||||
| Zahl der Dübel | n | - | 7 | 5 | ||
| Abstand der Dübel | a1 | mm | 100 | 80 | ||
| Winkel Kraftrichtung/Faserrichtung | α | ° | 0 | 0 | ||
| Dübeldurchmesser | d | mm | 20 | 16 | ||
| Festigkeit Dübelstahl | fuk | N/mm² | 360 | 360 | ||
| Holzdicke | t (a bei alter DIN) | mm | 130 | 130 | ||
| Holztyp (L)aub oder (N)adel |
- | n | n | |||
| Holz | ρk | kg/m³ | 350 | 350 | ||
| Stahlblechdicke Dübelhalterung/TD> | ts | mm | 10 | 10 | ||
| Erhöhung nach Formel (209)? | - | 1,25 | 1,25 | |||
| Anzahl unabhängiger Dübelgruppen/FONT> | - | 2 | 2 | |||
| Stützenlänge | h | m | 2,70 | 2,70 | ||
| Stützenfestigkeit | E*I | kNm² | 4400 | 4400 | ||
| neue DIN 1052 | ||||||
| fh0k | Formel (203) | 0,082(1-0,01d)ρk | N/mm² | 22,96 | 24,108 | |
| k90 | Formel(204/205) | 1,35+0,015d (N) 0,90+0,015d (L) |
- | 1,65 | 1,59 | |
| fhak | Formel (202) | fh0k/(k90*sin²(α)+cos²(α)) | N/mm² | 22,96 | 24,108 | |
| Myk | Formel (208) | 0,3 fuk d2,6 | N mm | 260676 | 145927 | |
| t*req (feste Halterung) | Formel (198) | 1,15*4 Wurzel(Myk/(fhk d)) | mm | 109,60 | 89,47 | |
| treq | 12.2.3 Punkt (3), (5), (6) | mm | 77,50 | 56,71 | ||
| AF | Bild X | - | 0,3698 | 0,4108 | ||
| R*k (feste Halterung - große Holzdicke) | Formel (197) | 2 Wurzel(Myk fhk d) | N | 21881,74 | 15005,08 | |
| R**k (gegebene Halterung) | 12.2.3 Punkt (3), (5), (6) | N | 15472,73 | 9511,47 | ||
| R***k (tatsächliche Holzdicke) | 12.2.3 Punkt (7) | N | 15472,73 | 9511,47 | ||
| Rk | Formel (209) | N | 19340,91 | 11889,34 | ||
| Kser | Tabelle G.1 | ρk1,5 * d/20 | N/mm | 6547,90 | 5238,32 | |
| vmax | Rk/Kser | mm | 3,0 | 2,3 | ||
| nd | siehe Artikel | - | 6,4 | 4,8 | ||
| φmax | 2 vmax/t | - | 0,0454 | 0,0349 | ||
| nef | Formel (210) | Min{n;n0,9*Wurzel(4)(a1/(10d)}(1-α/90)+n*α/90 | - | 4,85 | 3,58 | |
| Rges | Rk*nef | kN | 93,715 | 42,557 | ||
| zul M | Rges*t*AF*nd/n | kNm | 4,129 | 2,189 | ||
| Cd | Kser t2 nef AF /2 | kNm | 99,15 | 65,08 | ||
| zul M* | Gruppen * zul M | kNm | 8,258 | 4,378 | ||
| C*d | Gruppen * Cd | kNm | 198,30 | 130,16 | ||
| Stützenkopfverschiebung | h * φmax | cm | 12,27 | 9,43 | ||
| Knicklänge | knick(Stützenhöhe, Stützenfestigkeit,Steifigkeit) | m | 24,81 | 30,41 | ||
| alte DIN 1052 | ||||||
| zul σ | Tabelle 10 | MN/m² | 8,5 | 8,5 | ||
| B | Tabelle 10 | MN/m² | 51 | 51 | ||
| zul N* | Formel (3;4) | MIN{zul σ*a*d;B*d2} | N | 20400 | 13056 | |
| zul N | Punkt 5.10 | zul N* mal Erhöhungsfaktor | N | 25500 | 16320 | |
| v*max | Tabelle 13 | mm | 1,4 | 1,4 | ||
| vmax | v*max*Erhöhungsfaktor | mm | 1,75 | 1,75 | ||
| C (Verschiebungsmodul) | Tabelle 13 | 0,7 zul N* | N/mm | 14280 | 9139,2 | |
| areq | B d / zul σ | mm | 120 | 96 | ||
| AF | Bild X | - | 0,3333 | 0,3333 | ||
| φmax | 2 vmax/t | - | 0,0269 | 0,0269 | ||
| ef n | - | 6,67 | 5,00 | |||
| nd | siehe Artikel | - | 6,62 | 4,85 | ||
| Nges | kN | 136,000 | 65,280 | |||
| Nges/2 | kN | 68,0 | 32,6 | |||
| zul M | (Nges/2)*a*AF*nd/n | kNm | 2,79 | 1,37 | ||
| Cd (beachten 2 Scherfugen für C) | C t2 ef n AF /(2*2) | kNm | 134,1 | 64,4 | ||
| zul M | Gruppen * zul M | kNm | 5,58 | 2,75 | ||
| Cd | Gruppen * Cd | kNm | 268,15 | 128,71 | ||
| Stützenkopfverschiebung | cm | 7,27 | 7,27 | |||
| Knicklänge | knick(Stützenhöhe, Stützenfestigkeit,Steifigkeit) | m | 21,48 | 30,58 | ||
| zum Vergleich | ||||||
| weiterer Erhöhungs-Faktor | - | 1,15 | 1,15 | |||
| Belastung alte DIN | kN | 29,33 | 18,77 | |||
| mal Dübelzahl | kN | 205,28 | 93,84 | |||
| mal Dübellänge | kNm | 26,7 | 12,2 | |||
| Knicklänge Kragstütze | m | 5,40 | 5,40 | |||
| Impressum, Disclaimer | Startseite | letzte Änderung: 20.01.2006 |